Элементы теории кооперативных игр 183 2 страница

Поскольку эволюционная теория игр изучает популяции, "играющие в игры", она также полезна при изучении социальных норм и конвенций. Эволюция конвенций и социальных норм является примером игроков, обучающихся играть равновесие. Примеры включают популяцию потребителей, которые должны решить, какой тип товара покупать; популяцию работников, которые должны решить, какие усилия прилагать, и т. д.

Эволюционная теория игр дает положительный ответ на первый вопрос: во многих постановках игроки действительно играют равновесие по Нэшу. Таким образом, это дает оправдание равновесного анализа тогда, когда осмысленны эволюционные аргументы. Равновесие лучше всего рассматривать как устойчивое состояние сообщества, члены которого близоруко группируются "по направлению" к максимизирующему поведению. И это существенно контрастирует с более ранним взглядом (у которого нет достаточного фундамента), в соответствии с которым теория игр и равновесный анализ представляют исследование взаимодействия ультрарациональных агентов с "большим запасом" знаний.

Вопрос о том, какое равновесие играется, широко обсуждается особенно в литературе, касающейся "уточнений" (или "утончений") равновесия. Однако проблема их обоснования также относится к ним. Можно представить себе, например, что допускается пред-игровое общение, которое приводит к тому, что определяется, какое равновесие играется (скажем, все работники прикладывают максимум усилий, или, напротив, минимум, если, к примеру, общий выпуск определяется минимальным (среди всех работников) уровнем усилий). Такое оправдание равновесия, конечно, возможно и применимо к ряду приложений. Но это не покрывает все возможности, тем более, что неизбежны ситуации, когда договор может нарушаться, или, что просто может не быть возможности предварительного общения.

Второе оправдание самоосуществляющегося предсказания может проходить примерно следующим образом: если теоретически единственным образом предсказанное поведение игроков известно игрокам в игре, то она должна предсказывать равновесие по Нэшу. Трудность здесь в том, что такое оправдание требует теории, которая однозначно предсказывает поведение игроков, а в этом-то проблема как раз и состоит.

Оправдание с помощью "фокальной точки" (Т. Шеллинг) можно формулировать примерно так: "если есть очевидный путь играть в игре (либо в силу специфики постановки, либо в силу специальной структуры), то игроки будут знать, что будут делать другие игроки".

Наконец, игроки могут научиться играть некоторое равновесие. Для того, чтобы научиться играть некоторое равновесие, игроки должны иметь возможность повторять розыгрыш этой или, по крайней мере, близкой, игры, чтобы иметь возможность получать нужный опыт. Если только игроки узнали, как играют их оппоненты, и если игроки максимизируют, то они должны оказаться в равновесии по Нэшу. В этой истории с обучением есть два момента. Первый — игроки максимизируют. Второй — это то, что при условии максимизирующего поведения игроков, игроки могут узнать поведение своих оппонентов. Это включает в себя дополнительные нюансы обучения. Даже если игрок знает, как его оппоненты играли, они могут не знать, каково было наилучшее действие. Наконец, само обучение меняет обстановку, которую агенты пытаются узнать, причем процесс обучения весьма тонок.

Мы остановились здесь на некоторых моментах, которые представляются нам важными, и на которых мы считали необходимым остановиться в преддверии формального изложения теории.

Глава 1 Статические игры с полной информацией

1.1 Способы задания бескоалиционных игр

Основная часть курса будет посвящена теории бескоалиционных игр. Это ни в коей мере не означает, что отсутствует интерес экономистов к "некооперативному поведению". Напротив, в настоящее время заметен существенный интерес к попыткам объяснить, каким образом кооперация может возникнуть как результат поведения индивидов, преследующих свои цели. Наконец, есть целый ряд важных задач, где роль теории кооперативных игр весьма существенна. Им мы посвятим заключительную часть курса.

Теория бескоалиционных игр — это способ моделирования и анализа ситуаций, в которых оптимальные решения каждого участника (игрока) зависит от его представлений (или ожиданий) об игре его оппонентов. Как уже говорилось во введении, важнейшим моментом теории является акцент на то, что игроки не должны придерживаться произвольных представлений об игре своих оппонентов. Напротив, каждый игрок должен пытаться предсказать игру своих оппонентов, используя свои знания правил игры и исходя из предположений, что его оппоненты — сами рациональны, а потому пытаются сами также предсказать игру своих оппонентов и максимизировать свои собственные выигрыши.

Есть два способа задания игры. Первый — это позиционная форма[5] игры. Позиционная форма задает: (1) порядок ходов, (2) "альтернативы" (выбор), доступные игроку тогда, когда наступает очередь его хода; (3) информация, которую игрок имеет на каждом из его ходов; (4) выигрыши (всех) игроков, как функцию выбранных ходов;(5) вероятностные распределения на множестве ходов Природы.

Позиционная форма представляется деревом игры, которое можно рассматривать как обобщение дерева принятия решений, используемое в теории принятия решений, на случай нескольких игроков. Формальное определение мы приведем в гл. 2. "Древесная структура" описывает, какая вершина следует за какой, какой игрок имеет ход, в соответствующей вершине. Информация, которую имеют игроки, описывается с помощью информационных множеств (см. рис. 1). Если две вершины лежат в одном информационном множестве, то это означает, что игрок (в данном случае 3) не может сказать, какое из двух действий (Л или П) в действительности произошло (в этом смысле игрок не различает вершины дерева, лежащие в одном информационном множестве).

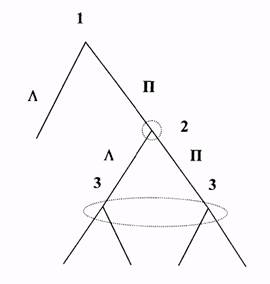
Рис. 1. Информационные множества отмечены пунктиром.

1, 2, 3 — номера игроков, имеющих право хода (здесь не указаны выигрыши в концевых вершинах дерева).

На рисунках 2 и 3 изображены недопустимые информационные множества: информационные множества не могут пересекаться (не различая вершины одного информационного множества и вершины другого информационного множества, которое пересекается с первым, игрок тем самым не различает вершины, лежащие в объединении этих информационных множествах); в вершинах одного информационного множества — множества доступных игроку альтернатив должны совпадать (иначе игрок сможет различать вершины информационного множества, а стало быть, различать действия, предшествовавшие его ходу).

Рис 2 Рис.3.

Рис. 4. В концевых вершинах указаны выигрыши игроков.

Приведем элементарный пример. Рассмотрим следующую игру: первый игрок выбирает одну из трех цифр — 1,2 или 3. Затем второй игрок, не зная выбора первого игрока, также выбирает одну из трех цифр — 1, 2, 3. Если сумма выбранных цифр четна, то первый игрок выигрывает у второго один рубль (доллар, фунт...). Если сумма — нечетная, то наоборот — выигрывает второй. Дерево соответствующей игры изображено на рис. 4.

На рис.5 изображена модификация этой игры, в которой второму игроку становится известно либо, что первый игрок выбрал цифру 2, либо, напротив, что цифру 2 он не выбрал.

Рис. 5.

Мы вернемся к позиционной форме в гл. 2 (поскольку в этой главе нас интересуют статические игры с полной информацией, для которых позиционная форма — это некоторое излишество), а теперь перейдем ко второй возможной форме представления игры — нормальной или стратегической форме, которая "суммирует" позиционную игру в трех элементах: множестве игроков I, множестве стратегий каждого игрока и функции выигрышей, ставящей в соответствие каждому набору стратегий игроков соответствующие выигрыши игроков.

1.2 Игры в нормальной форме

Итак, игра в нормальной (или стратегической) форме[6] — это тройка {I, S = Пi{Si}_iÎI u = (u₁,…,u_n)}, где I = {1,..., n} — множество игроков, Si — множество стратегий (ходов)[7], доступных игроку i = 1,..., n,

ui: S = П_iÎI Si ® R¹ — функция выигрышей игрока i, ставящая в соответствие каждому набору стратегий s = (s₁,..., s_n), называемому также ситуацией, выигрыш этого игрока[8].

Стандартный пример здесь — дуополия по Бертрану и по Курно, когда стратегии

— это цены или объемы выпуска, соответственно, а выигрыши — это прибыль (см. п. 1.8-1.10).

Важным предположением, которое играет ключевую роль в теории, состоит в предположении, что все игроки рациональны, в том смысле, что каждый игрок рассматривает имеющиеся в его распоряжении альтернативы, формирует представления относительно неизвестных параметров, имеет четко определенные предпочтения и выбирает свои действия в результате некоторого процесса оптимизации (максимизации своей целевой функции). Более того, не менее существенным является факт общеизвестности (общего знания)[9] рациональности игроков, т. е. все игроки не только рациональны, но и знают, что другие игроки рациональны, что все игроки знают, что все игроки знают, что они рациональны и т. д. Формальное определение общеизвестности см. Aumann (1976).

Замечание 1.2.1. В последние годы появилось значительное число работ, посвященных исследованию моделей ограниченной рациональности. Основная мотивация этих работ — неудовлетворенность теорией, оперирующей с "совершенно рациональным человеком", поскольку мы является свидетелями весьма частого несоответствия реального поведения людей предположению "совершенной рациональности". Идея моделирования ограниченной рациональности восходит к работам Герберта Саймона (Simon (1955, 1956), см. также Simon (1972, 1976)). Обсуждение проблем, связанных с моделировнием ограниченной рациональности можно найти, например, в книге Rubinstein (1998). Различные взгляды на проблемы моделирования рациональных и ограниченных рациональных игроков изложены в работах Binmore (1987, 1988), Auman (1996).

Обратимся к тому случаю, когда I = {1,2} и множества стратегий каждого из двух игроков — конечны. В этом случае игру можно "изобразить" с помощью матрицы (см. рис.6), где М = ïS_iï — число возможных стратегий игрока 1, К =ïS₂ï —число возможных стратегии игрока 2,

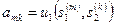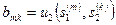, , k = l,...,K, m = 1,...,M.

Эту же игру можно представить в виде двух матриц (поэтому такие игры называются часто биматричными), элементами которых являются элементы а_mk и b_mk, соответственно.

Для конечной антагонистической игры, т. е. игры двух лиц такой, что u₁(s1, s2) = -u₂(s1, s2) для всех siÎSi, i = 1,2, справедливо равенство а_mk = -b_mk, для всех m и k,

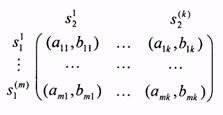
Рис. 6.

а поэтому такая игра может быть задана только одной матрицей (а_mk) m=1,...,M, k=1,..., К и поэтому конечные антагонистические игры называются матричными (см. подробнее Дополнение (Раздел 1.13)).

Смешанная стратегия[10] si — это вероятностное распределение на множестве чистых стратегий Si. (Мотивацию введения смешанных стратегий мы оставляем на будущее). Рандомизация каждым игроком своих стратегий статистически независима от рандомизаций его оппонентов, а выигрыши, соответствующие профилю (набору) смешанных стратегий — это ожидаемое значение выигрышей соответствующих чистых стратегий (т.е. речь здесь идет об ожидаемой полезности). Одна из причин, по которой мы сосредотачиваемся на конечном случае — стремление избежать "осложнений", связанных с теорией меры.

Будем обозначать пространство смешанных стратегий i-ого игрока через Si, а s_i(s _i) — вероятность того, что выбирается стратегия s;. Пространство наборов смешанных стратегии

элементы которого мы будем обозначать через s. Носитель смешанной стратегии si — это множество тех чистых стратегий, которым "приписана" положительная вероятность.

Определение 1.2.1. Если S_i — конечное множество чистых стратегий игрока i, то смешанная стратегия s_i: S_i ® [0, 1] ставит в соответствие каждой чистой стратегии s_iÎS_i вероятность si(si) ³ 0 того, что она будет играться, причем

(Обратим внимание на то, что индекс i означает здесь, что речь идет о стратегии игрока i. Поэтому, если мы будем говорить о разных стратегиях игрока i, то мы будем обозначать их s_i, s'_i, s"_i,...).

Нетрудно заметить, что множество смешанных стратегий игрока i — это (k_i - 1)-мерный симплекс, где k_i — число чистых стратегий i-го игрока.

Выигрыш игрока i, соответствующий профилю (набору) стратегий s, есть

(2.1)

(поскольку на наборах чистых стратегий значения этой функции совпадают со значениями исходной функции выигрышей u_i, мы сохраняем то же обозначение).

Важно отметить, что выигрыш i-ого игрока есть линейная функция от вероятностей s_i, а также является полиномом от профиля, а потому непрерывен. Наконец, чистые стратегии являются вырожденными смешанными стратегиями, приписывающими вероятность 1 данной чистой стратегии и вероятность 0 — остальным.

Определение 1.2.2. Смешанным расширением игры Г = {I, S, u} называется игра

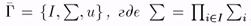
а, u(s), где sÎS, определяется равенством (2.1).

Пример. Рассмотрим игру, изображенную на рис. 7.

L M R

Рис. 7.

Пусть s1 = (1/3, 1/3, 1/3) (это означает, что смешанная стратегия игрока 1 приписывает ему играть стратегии u, m и d с вероятностями 1/3), s₂ = (0, 1/2, 1/2) (эта смешанная стратегия игрока 2 предписывает играть стратегии М и P с равными вероятностями и не играть стратегию L вовсе). В данном случае мы получаем

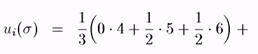
+ 1/3×(0×2 +1/2*8 + ½ *3) + 1/3×(0*3 + ½*9 +1/2*2) = 11/2,

u₂(s) = 27/6.

1.3 Доминируемые стратегии

Посмотрим внимательно на приведенную выше игру (рис.7). Независимо от того, как играет игрок 1, R дает игроку 2 строго больший выигрыш нежели М. В этом смысле стратегия М строго доминируема, поэтому ясно, что рациональный игрок 2 не должен играть М. Далее, если игрок 1 знает (т.к. он сам рационален и знает, что другой рационален...), что 2 не будет играть М, то для него и будет лучше, чем га или d. Наконец, если игрок 2 знает, что игрок 1 знает, что игрок 2 не будет играть М, то игрок 2 знает, что 1 будет играть и, а тогда 2 должен играть L. Этот процесс — последовательное удаление строго доминируемых стратегий (мы дадим позднее строгое определение и соответствующий экономический пример). Вопрос, естественно возникающий здесь: "А не зависит ли множество стратегий, выдержи­вающих такое исключение доминируемых стратегий, от порядка исключения?" К счастью, нет, и дело здесь в том, что если стратегия s_i строго хуже чем s' для всех стратегий оппонента из множества D, то она хуже чем s' и для любого подмножества множества D.

Посмотрим теперь на следующую игру (см. рис. 8)

Рис. 8.

Здесь М не доминируется строго стратегией u, и М не доминируется строго стратегией D. Однако, если игрок 1 играет u с вероятностью 1/2 и D — с вероятностью 1/2, он обеспечивает себе выигрыш 1/2 независимо от того, как играет игрок 2. Следовательно, чистая стратегия может строго доминироваться смешанной стратегией, даже если она не доминируется строго никакой чистой стратегией.

Введем следующие обозначения: пусть iÎI, тогда через s_-i Î S_-i будем обозначать набор стратегий игроков из I\{i}, (s'_i, s_-i) обозначает набор стратегий (s₁, …, s_i-1, s'_i, s_i+1, …, s_n). Аналогично, для смешанных стратегий (s'_i, s_-i) — это (s₁, …, s_i-1, s'_i, s_i+1, …, s_n). (Заметим, что в этих обозначениях s = (s_i, s_-i)).

Определение 1.3.1 Чистая стратегия S_i игрока i в игре Г строго доминируема (строго доминируется), если существует другая чистая стратегия s'_i такая, что

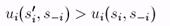(3.1)

для всех s_-i Î S_-i.

В этом случае говорят, что стратегия s'_i доминирует стратегию s_i. Стратегия s_i. слабо доминируется, если существует такая s'_i, что (3.1) выполняется как нестрогое неравенство, но хотя бы для одного набора s_-i - неравенство строгое.

Аналогично определение и для смешанных стратегий:

Определение 1.3.2. Смешанная стратегия s_i строго доминируется в игре 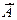_; если существует другая стратегия s'_i такая, что для всех s _-iÎS_-i выполняется

Стратегия s_i называется строго доминирующей стратегией для игрока i в игре 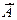, если она строго доминирует любую другую стратегию из S_i.

Заметим, что для того, чтобы проверить, что s_i строго доминируется стратегией s'_i, нам нужно посмотреть на "поведение" этих двух стратегий против чистых стратегий оппонентов игрока i.

Формально:

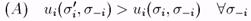
тогда и только тогда, когда

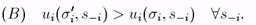
Действительно: рассмотрим разность

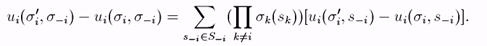
Тогда если (В), то (А), т.к. все [u_i(s'_i, s_-i) — u_i(s_i, s_-i)] > 0. (В) следует из (А), т.к. s_-i — вырожденный случай s_-i.

Задача. Докажите, что если чистая стратегия s_i является строго доминируемой, то таковой же является и любая стратегия, использующая s_i с положительной вероятностью.

Однако смешанная стратегия может быть строго доминируемой даже, если она использует с положительной вероятностью чистые стратегии, которые даже не слабо доминируемы. Действительно, рассмотрим следующую игру (рис.9).

Рис. 9.

Стратегия первого игрока (1/2, 1/2,0) дает ожидаемый выигрыш вне зависимости от того, что играет игрок 2, а следовательно, строго доминируется стратегией D.

Естественно, что строго доминируемые стратегии надо удалять. Если игра разрешима в смысле последовательного удаления строго доминируемых стратегий, т. е. каждый игрок остается с единственной стратегией, как в нашем первом примере, то, получившаяся ситуация будет хорошим кандидатом для предсказания того, как будет проходить игра.

Вернемся к игре, изображенной на рис. 7. Нетрудно убедиться в том, что здесь в результате последовательного удаления строго доминируемых стратегий остается пара стратегий (u, L). На первом шаге удаляется стратегия М (она доминируется стратегией R). Затем удаляется стратегия m (доминируемая стратегией u).На третьем шаге удаляется стратегия d (доминируется стратегией u). Наконец, на последнем шаге удаляется R.

Но, даже если такие ситуации представляют собой хорошие кандидатуры, все не обязательно произойдет в соответствии с их "предписанием", особенно если выигрыши могут принимать "экстремальные" значения.

Рассмотрим, например, следующую игру (рис. 10).

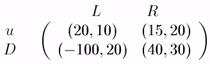
Рис. 10.

Очевидно, что здесь стратегия L доминируется стратегией R, а потому ситуация (D,R) является хорошим кандидатом. Но... Проигрыш игрока 1 в ситуации (_D, L) слишком велик, поэтому вполне можно допустить, что игрок 1 может не рискнуть сыграть стратегию d (допуская, например, возможность случайной ошибки игрока 2).

Все, конечно, изменится, если игроки могут договориться до того, как принять решение. В этом случае, конечно, все уже будет зависеть от "силы" договоренности.

1.4. Последовательное удаление слабо доминируемых стратегий

Рассмотрим следующую известную игру "Море Бисмарка". Предыстория события такова: 1943г. Адмирал Imamura получил приказ доставить подкрепление по морю Бисмарка на Новую Гвинею. В свою очередь адмирал Кеnnеу должен был воспрепятствовать этому. Imamura должен был выбрать между Северным (более коротким) и Южным маршрутами, а Кеnnеу — решить куда посылать самолеты, чтобы разбомбить конвой. Причем в течение одного дня самолеты могут бомбить лишь на одном из двух направлений — либо на Северном, либо на Южном маршрутах (но не на двух). Поэтому, если Кеnnеу посылает самолеты в сторону неправильного маршрута, то они могут вернуться, но число дней, когда возможна бомбежка, уменьшается. Описываемая ситуация моделируется следующей игрой. Считаем, что Северный маршрут займет 2 дня, а Южный — 3. (См. рис. 11).

Рис. 11.

Вообще говоря — это матричная игра, т. е. антагонистическая игра с конечным множеством стратегий у каждого игрока. Ни один игрок не имеет доминирующей стратегии. Но здесь можно говорить о слабом доминировании: для Imamur'ы стратегия Юг слабо доминируема, так как для любой стратегии Кеппеу проигрыш Imamur'ы (число дней, когда конвой будет подвергаться бомбордировкам) не меньше для Ю, чем для С, но для стратегии Кеnnеу Ю — проигрыш при С строго меньше, чем при Ю.

Последовательное (итерированное) удаление слабо доминируемых стратегий проходит следующим образом: исключается одна из слабо доминируемых стратегий одного из игроков, затем из оставшихся стратегий исключается одна из слабо доминируемых стартегий и т. д.

Представим себе, что Кеnnеу понимает это и считает, что Imamura выберет Север. В этой новой ситуации Кеnnеу имеет уже доминирующую стратегию — Север. Это и дает нам равновесие при последовательном удалении доминируемых стратегий. (В действительности, так и случилось: 2-5марта 1943 г. ВВС США и Австралии атаковали японский конвой, который шел по Северному пути и потопили все транспортные корабли и 4 эсминца: из 7000 чел. до Новой Гвинеи добрались 1000.)

Процедура последовательного удаления слабо доминируемых стратегий аналогична удалению строго доминируемых стратегий. Однако здесь есть одно весьма значительное отличие. А именно, множество стратегий, которые выдерживают последовательное удаление слабо доминируемых стратегий (то есть остаются) может зависеть от порядка удаления стратегий.

Действительно, рассмотрим следующую игру (рис. 12).

Рис. 12.

Если вначале удаляется u (слабо доминируется М), а затем L (слабо доминируется R), то мы приходим к исходу (2,1) (второй игрок выбирает R). Если же вначале удаляется D (слабо доминируется М), а затем R (слабо доминируется L), то мы приходим к исходу (1,1).

Рассмотрим несколько примеров. Мы начнем со знаменитой Дилеммы Заключенного — в некотором смысле чрезвычайно простой игры, которая в разных формулировках встречается в большинстве учебников по теории игр, которая приводится едва ли не в самом начале каждого курса и которую многие сразу же вспоминают, когда слышат словосочетание "теория игр".

Дилемма Заключенного. Ставший почти хрестоматийным сюжет этой стилизованной истории таков. Двое подозреваемых в совершении тяжкого преступления арестованы и помещены в одиночные камеры, причем они не имеют возможности передавать друг другу какие-либо сообщения. Их допрашивают поодиночке. Если оба признаются в совершении преступления, то им грозит, с учетом их признания, тюремное заключение сроком по 6 лет каждому. Если оба будут молчать, то они будут наказаны за совершение какого-то незначительного преступления и получат в этом случае по 1 году тюремного заключения. Если же один из них сознается, а другой — нет, то первый, за содействие следствию, будет вовсе освобожден от наказания, тогда как второй будет приговорен к максимально возможному за данное преступление наказанию — 10-летнему тюремному заключению.

Описанная история может быть представлена следующей игрой (рис. 13).

Рис. 13.

Здесь нетрудно убедиться в том, что стратегия "молчать" является строго доминируемой для каждого игрока (еще раз напомним, что они рациональны), поэтому каждый игрок выберет стратегию "сознаться". В результате оба заключенных получат по 6 лет тюремного заключения.

Как мы увидим ниже ситуация ("сознаться", "сознаться"), естественно, является ситуацией равновесия по Нэшу. При этом мы сразу же сталкиваемся с бросающейся в глаза проблемой: получающийся исход очень плохой — он дает максимальный суммарный срок заключения (разумеется, мы подчеркиваем это еще раз, не следует забывать предположение о рациональности игроков, поскольку здесь исключаются из рассмотрения проблемы предательства, и т. д.). Это послужило толчком к многочисленным исследованиям этой игры, поскольку, например, естественным желанием было бы получить в качестве исхода этой игры (или ее модификаций) ситуацию ("молчать", "молчать"), дающую каждому заключенному лишь по одному году заключения.

Следующая игра имеет уже ярко выраженный экономико-политический подтекст, хотя разделяет с дилеммой заключенного упомянутую выше специфику, поэтому мы позволим себе сохранить то же название:

" Дилемма заключенного - 2 ". Рассмотрим две страны добывающие нефть, которые мы назовем, скажем, А и В. Эти две страны могут кооперироваться, договариваясь об объемах ежедневной добычи нефти, ограничиваясь, к примеру, добычей 2 млн. баррелей нефти в день для каждой страны. С другой стороны, страны могут действовать некооперативно, добывая, скажем, по 4 млн. баррелей в день. Такая ситуация может быть представлена следующей игрой, в которой указаны прибыли стран, в зависимости от их объемов добычи нефти (рис. 14).

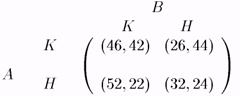
Рис. 14.

Эта картина достаточно типична для картеля, когда у каждого из членов картеля есть стимул отклониться от договора, чтобы за счет увеличения объемов продаж получить дополнительную прибыль.

Легко видеть, что и здесь у каждого из игроков есть доминирующая стратегия — "не кооперироваться". В результате страны получают прибыль 32 и 24 (млн. долларов в день), что гораздо меньше, нежели в ситуации кооперативного поведения.

Феномен, с которым мы столкнулись в этом примере, аналогичен дилемме заключенного, и именно поэтому второй пример мы также назвали " дилеммой заключенного ": оба игрока играют свои доминирующие стратегии, максимизируя тем самым свои выигрыши, но в то же время исход для каждого из них хуже, нежели в ситуации, когда оба следуют доминируемым стратегиям.

Можно ли достичь "кооперативного поведения" в дилемме заключенного? Как мы увидим в следующей главе — да.

Здесь мы ограничимся лишь еще одним примером на эту же тему.

"Дилемма заключенного - 3". Предположим, что есть 2 работника, которые могут "работать" (s_i = 1) и "увиливать" (s_i = 0) (s_i — уровень усилий, которые прикладывает работник i). Суммарный выпуск "команды" 4(s₁+s₂) делится поровну между работниками. Каждый работник несет издержки равные 3, если работает, и равные 0, если увиливает. Соответствующая матрица изображена на рис. 15.

Дата добавления: 2014-10-31