Элементы теории кооперативных игр 183 3 страница

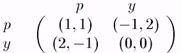
Рис. 15.

"Работать" — строго доминируемая стратегия для каждого работника.

Аукцион второй цены. У продавца есть одна единица неделимого товара. Есть п потенциальных покупателей, которые оценивают товар, соответственно, в 0 < v₁ < … < v_n и эти оценки являются "общеизвестными". Покупатели одновременно делают свои заявки (назначают цену) s_iÎ[0, +¥). Назначивший максимальную заявку получает товар и платит вторую цену, т. е. если игрок i выигрывает (s_i >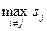), то его полезность есть u _i = v_i — 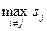, а остальные ничего не получают и ничего не платят (т. е. u _j = 0). Если несколько покупателей назначают высшую цену, то товар распределяется случайным образом (например, равновероятно).

Легко убедиться в том, что стратегия назначения своей оценки (s_i = v _i) слабо доминирует все остальные. Действительно, пусть r_i = 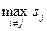. Пусть s_i > v_i. Тогда, если r_i ³ s_i, то r -ый участник получает 0, что он получил бы и при s_i = v_i. Если r_i £ v_i, то он получает v_i - r _i, что он опять же получает, назначив v_i. Если теперь v_i < r _i < s _i, то его полезность v_i - r _i < 0, а если бы он назвал v_i, то он бы получил 0. Аналогично и для s_i < v_i: если r_i£s_i или r_i ³ v_i, то он получает ту же полезность, назвав v_iвместо s_i. Если же s_i < r _i < v_i, то он упускает возможность получить положительную полезность.

Полезно в данном случае заметить, что поскольку назначение собственной оценки есть доминирующая стратегия, то не играет роль, имеют ли покупатели информацию об оценках других.

Мы вернемся к аукциону второй цены в п. 1.6.

1.5 Рационализуемые стратегии

Мы обсуждали исключение строго доминируемых стратегий, исходя из того, что рациональный игрок никогда не выбрал бы такую стратегию, вне зависимости от того, как играют его оппоненты. Однако "общее знание" структуры игры и того, что игроки рациональны, позволяет исключить больше, нежели просто последовательно удалить строго доминируемые стратегии, причем здесь опять же важную роль играет "общее знание". Далее мы рассматриваем смешанное расширение 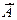игры Г.

Определение 1.5.1. Стратегия s_i является лучшим ответом игрока i на набор стратегий оппонентов s_-i, если u(s_i, s_-i) ³ u(s_i^', s_-i) при любых s_i^'ÎS_i. Стратегия s_i является "никогда не лучшим" ответом [11] (далее НЛО), если не существует s_-i, для которых она была бы лучшим ответом.

Конечно же игрок не будет играть стратегию, которая является "никогда не лучшим ответом".

Ясно, что строго доминируемая стратегия является "никогда не лучшей". Разумеется, может случиться, что стратегия будет "никогда не лучшим ответом", даже если она не является строго доминируемой (мы еще вернемся к этому). Таким образом, удаляя "никогда не лучшие ответы", мы должны удалить по крайней мере и все стратегии, удаляемые при итерированном (последовательном) удалении строго домиинируемых стратегий. Более того, предполагая "общее знание", мы можем итерировать удаление "никогда не лучших ответов". Рациональный игрок не должен играть НЛО, как только он исключает возможность того, что его противники могут играть НЛО и т.д.

Стратегии, остающиеся после такого итеративного удаления, — это те стратегии, которые рациональный игрок может оправдать, или рационализовать, разумеется, при некоторых разумных предположениях о выборе своих противников.

Определение 1.5.2. Стратегии в S_i, которые выдерживают последовательное удаление НЛО назыаются рационализуемыми стратегиями [12].

Понятие рационализуемых стартегий было введено независимо Бернхеймом и Пирсом (Bernheim, 1984; Реагсе, 1984).

Можно показать, что также, как и при последовательном удалении строго доминируемых стратегий, порядок удаления не существенен. Заметим, что множество рационализируемых стратегий не может быть шире, чем множество стратегий, "выживающих" при последовательном удалении строго доминируемых стратегий, поскольку на каждом шаге процесса, определяющего множество рационализируемых стратегий, все стратегии, строго доминируемые на данном шаге, удаляются.

Пример (Osborn, Rubinstein) (см.рис. 16)

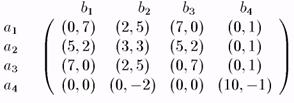
Рис. 16.

На 1 шаге исключения удаляется стратегия b₄, т. к. она является НЛО, поскольку она строго доминируется смешанной стратегией (1/2, 0, 1/2,0) или (2/3,1/3,0,0). Как только исключено b₄ можно исключить а₄, т.к. она строго доминируется а₂ (поскольку b₄ удалена). Но дальше мы уже не можем удалить ни одну стратегию, т.к. a₁ — лучший ответ на b₃, a₂ — на b₂ и а₃ — на b₁. Аналогично остаются b1, b2, b3. Таким образом, множество рационализуемых чистых стратегий есть {a1, a2, a3} для игрока 1 и (b1, b2, b3) — для игрока 2.

Для каждой рационализуемой стратегии, игрок может построить последовательность "оправданий" своего выбора, без ссылок на убеждение в том, что другой игрок не будет играть НЛО стратегию. Например, в этой игре игрок 1 может оправдать выбор а2 убеждением, что игрок 2 будет играть b2, которое игрок 1 может оправдать убеждением, что игрок 2 будет думать, что он собирается играть а2, что осмысленно, если игрок 1 убежден, что игрок 2 думает, что он, игрок 1, думает, что игрок 2 будет играть b2 и т. д.

Мы отметили, что множество рационализуемых стратегий не больше, чем множество стратегий, остающихся после последовательного удаления строго доминируемых стратегий. Однако в случае двух игроков (n = 2) эти два множества совпадают, так как в игре 2-х лиц (смешанная) стратегия s_i является лучшим ответом на некоторую стратегию противника, если s_i не является строго доминируемой. Если чистая стратегия s_i игрока i является НЛО для любой смешанной стратегии оппонента, тогда s_i строго доминируется некоторой смешанной стратегией s_iÎS_i.

Посмотрим это на примере (Mas-Colell, Whinston, Green) (см. рис. 17).

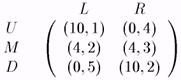
Рис. 17.

У игрока 1 — три стратегии U, М и D. U лучшая против L, но худшая против R, D лучшая против R, и худшая — против L. С другой стороны М "относительно неплоха" и против L и против R. Ни одна из этих трех стратегий не доминируется никакой другой. Но если разрешить игроку 1 рандомизацию, то игра U и D с вероятностями 1/2 каждая дает игроку 1 ожидаемый выигрыш 5, вне зависимости от стратегии второго игрока, тем самым строго доминируя М.

Предположим, что выигрыши от использования стратегии М изменены так, что М не является строго доминируемой. Тогда выигрыши от М лежат где-то выше, чем линия, соединяющая точки, соответствующие стратегиям U и D. Здесь оси соответствуют ожидаемым выигрышам игрока 1 в случае, если игрок 2 играет R (ось ur) и L (ось u_R) (см. рис.18).

Линия аb - это множество

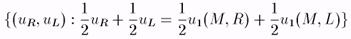
Является ли М здесь лучшим ответом? ДА.

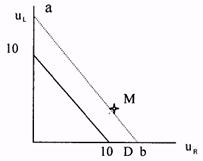
Рис. 18.

Действительно, заметим, что если игрок 2 играет R с вероятностью s₂(R), тогда ожидаемый выигрыш игрока 1 от выбора стратегии с выигрышами (u_R, u_L) есть s₂(R)×u_R + (1 — s₂ (R))×u_L. Легко видеть, что М —это лучший ответ на s₂(R) = 1/2; он дает ожидаемый выигрыш, строго больший, чем ожидаемый выигрыш, достижимый с помощью стратегий U и/или D. (В случае n > 2 это уже не так: могут быть стратегии, являющиеся НЛО, но не являющиеся строго доминируемыми; это связано с тем, что рандомизация независима).

1.6 Равновесие по Нэшу

Мы начнем со случая, когда рассматривается исходная игра Г, а к смешанному расширению обратимся несколько позже.

Определение 1.6.1 Набор стратегий s = (s₁,..., s_n) образует равновесие по Нэшу (или ситуация s = (s₁,..., s_n) является равновесной по Нэшу) в игре Г = {I, {Si}, {ui}}, если для любого i = 1,... n

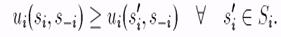
Иными словами, если игрок в одиночку решает отклониться от выбранной стратегии, то он разве лишь ухудшит свое положение.

В ситуации равновесия по Нэшу, выбранная каждым игроком стратегия является лучшим ответом на стратегии, действительно "играемые" соперниками. В этом принципиальное отличие от рационализируемости, которая следует из общего знания о рациональности друг друга и структуры игры, и требует только, чтобы стратегия игроков была лучшим ответом на некоторую разумную гипотезу о том, что его противник будет играть, причем под разумностью понимается, что гипотетическая игра его противников может быть также оправдана. Таким образом, равновесность по Нэшу добавляет к этому требование того, чтобы игроки были правы в своих гипотезах. (Далее мы для краткости будем писать р.Н. для обозначения равновесия по Нэшу).

Разумеется, полученные нами ситуации в рассмотренной ранее дилемме заключенного (во всех ее вариантах) являются равновесными по Нэшу.

Пример. "Семейный спор". Этот пример также относится к числу традиционных примеров, различные вариации которого встречаются в большинстве учебников. История примерно такова. Он и Она независимо (мы оставляет в стороне вопрос о разумности или неразумности подобной постановки вопроса) решают, куда пойти — на балет (Б), или футбол (Ф). Если они вместе пойдут на футбол, то Он получит больше удовольствия, чем Она; если они вместе пойдут на балет, то — наоборот. Наконец, если они окажутся в разных местах, то они не получат никакого удовольствия. Рассматриваемая ситуация моделируется следующей игрой (см. рис. 19):

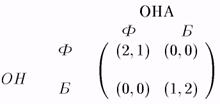
Рис. 19.

Легко видеть, что здесь есть 2 равновесия по Нэшу в чистых стратегиях — (Ф, Ф) и (Б, Б). Мы увидим ниже, что в этой игре есть еще одно равновесие по Нэшу — в смешанных стратегиях.

Пример. Рассмотрим следующую игру (рис. 20)

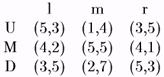
рис. 20.

Ясно, что здесь набор стратегий (М, m) образует равновесие по Нэшу. Если игрок 1 выбирает М, то у 2-ого лучший ответ — m и наоборот.

Пример. Вернемся к примеру, касавшемуся рационализуемости (рис. 16). В нем существует единственная (даже если разрешены смешанные стратегии) ситуация равновесия по Нэшу — (а₂, b₂).

Этот пример иллюстрирует общее взаимоотношение между р.Н. и рационализуемыми стратегиями. Каждая стратегия, являющаяся частью р.Н., рационализуема, поскольку каждая стратегия игрока в ситуации р.Н. может быть "оправдана" равновесными стратегиями других игроков. Таким образом, равновесие по Нэшу предсказывает как минимум не хуже, чем рационализуемость, впрочем очень часто эти предсказания оказываются значительно более "четкими".

Очень удобно следующее переопределение равновесия по Нэшу. Введем следующее многозначное отображение "лучших ответов"

b_i:S_-i ® S_i (в игре Г):

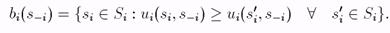
Тогда ситуация (s₁,..., s_n) является равновесием по Нэшу в игре Г, если s_i Î b_i(s_-i) для " i = 1,..., n.

Что же можно сказать по поводу того, а почему собственно нам нужно заниматься р.Н.? На самом деле это один из проблемных вопросов теории игр, несмотря на очень широкое использование р.Н.

(1) Равновесие по Нэшу, как последовательность рациональных выводов (умозаключений). Хотя это часто используется в качестве довода, тем не менее, мы видим, что следствие общего знания — это необходимость играть рационализируемые стратегии. Рациональность не обязательно ведет к правильности предсказания.

(2) Равновесие по Нэшу как необходимое условие, если есть единственный предсказуемый исход игры. Если игроки думают и разделяют представления о том, что существует очевидный (в частности, единственный) способ играть игру, то это должно быть р.Н. Разумеется, этот аргумент подходит, если существует единственное предсказание, как игроки будут играть. Однако, вспомнив рационализуемость, мы придем к выводу, что этого недостаточно. Поэтому, этот аргумент полезен, если есть действительно повод считать некоторый набор стратегий очевидным способом сыграть в игру.

(3) Фокальные точки. Иногда случается так, что определенный исход является тем, что Шеллинг (1960) называет фокальным исходом (2-х человек просят назвать независимо какое-то место встречи, и если их выбор совпадет, то получают выигрыш). Это, конечно, явный кандидат, но только если он р.Н.

(4) Равновесие по Нэшу как самофорсирующее соглашение. Если игроки перед игрой имеют возможность предварительных необязыващих переговоров. Если они согласились на какой-то исход, то это, конечно, очевидный кандидат.

Чтобы он стал самофорсирующим нужно, чтобы он был р.Н. Хотя даже, если они договорились играть р.Н., они все равно могут отклониться, если ожидают, что другие могут тоже уклониться.

(5) Равновесие по Нэшу как устойчивое социальное соглашение. Определенный способ играть в игру может возникнуть во времени, если игра разыгрывается повторно и появляется некоторое устойчивое социальное соглашение. Если это так, то для игроков может быть "очевидным", что это соглашение будет поддерживаться. Это соглашение становится, так сказать, фокальным.

Более подробное обсуждение этой проблематики можно найти, например, в учебнике Mas-Colell, Whinston, Green.

1.7 Равновесие по Нэшу в смешанных стратегиях

Примеры, которые мы рассмотрели выше, продемонстрировали, что даже в очень простых играх равновесие по Нэшу в чистых стратегиях может быть не единственным. Однако, как мы увидим сейчас, равновесия в чистых стратегиях может не существовать вообще.

Пример. "Игра в орлянку" или "Орел или решка". 2 игрока одновременно, независимо выбирают либо "решку", либо "орла". Если их выбор различен, то первый игрок платит второму 1 рубль (доллар, и т.д.), если их выбор одинаков, то наоборот — второй платит первому столько же. Соответствующая игра имеет следующий вид (см. рис. 21).

Рис. 21.

Легко видеть, что в этой игре нет равновесия по Нэшу в чистых стратегиях, так как в любой ситуации одному из игроков выгодно отклониться от выбранной стратегии. Однако, как мы увидим, пара смешанных стратегий s1 = (1/2, ½), s2 = (1/2, ½), в которых каждый из игроков играет свои чистые стратегии с равными вероятностями, образует равновесие по Нэшу в смешанных стратегиях.

Определение 1.7.1 Ситуация (набор смешанных стратегий) s = (s₁,.., s_n) является равновесием по Нэшу в игре 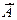= {I, {S_i}, {u_i}}, если для любого i = 1, …, n

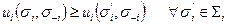
Предложение 1.7.1 Пусть S⁺_iÌ S_i — множество чистых стратегий, которые игрок i играет с положительной вероятностью в ситуации) s = (s₁,.., s_n). Ситуация s является р.Н. в смешанном расширении 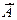игры Г тогда и только тогда, когда для всех i = 1,..., п

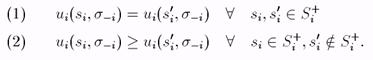
Доказательство. Необходимость. Если бы одно из этих условий не выполнялось для некоторого i, то нашлись бы две стратегии s_iÎ S⁺_i и s'_iÎSi: 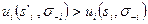, а значит, это не р.Н.

Достаточность. Предположим теперь, что (1) и (2) выполнены, но s - не р.Н. Тогда существует игрок i и стратегия s'i такая, что

Но если это так, то существует чистая стратегия s’_i, которая играется с положительной вероятностью при s’_i и для которой 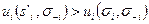. Так как 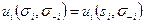для любой s_iÎ S⁺_i, это противоречит (1) и (2).

Таким образом, необходимые и достаточные условия того, что ситуация s — р.Н., состоит в том: 1) что каждый игрок при данном распределении стратегий, которые играют его противники, безразличен между чистыми стратегиями, которые он играет с положительной вероятностью; 2) что эти чистые стратегии не хуже тех, которые он играет с нулевой вероятностью.

Это свойство можно использовать для нахождения смешанного равновесия по Нэшу (т.е. равновесия по Нэшу в смешанных стратегиях).

Пример. Рассмотрим следующую игру (рис.22).

Рис. 22.

Очевидно, что ситуации (А,А) и (В,В) являются равновесными по Нэшу (в чистых стратегиях). Найдем равновесия по Нэшу в смешанных стратегиях. Предположим, что в таком равновесии игрок 1 играет смешанную стратегию (р, 1 - р), а второй — (q, 1 - q), причем 0 < р, q < 1.

Тогда, учитывая приведенное предложение мы, получаем, что ожидаемый выигрыш игрока 2 от игры А есть 1000р + 0×(1 - р), а от игры В есть 100 *(1 - р) + 0×р, а значит

1000×р + (1 - р)×0 = 100×(1 - р) + 0×р.

Отсюда 1100р = 100 и следовательно р = 1/11. Аналогично, q = 1/11. Заметим, что в соответствии с предложением 1.7.1 у игроков в данном примере нет предпочтений относительно вероятностей, которые они приписывают своим стратегиям. Эти вероятности определяют "равновесное рассмотрение": необходимость сделать другого игрока безразличным относительно его стратегий.

Пример. Вернемся к игре "Семейный спор". Поступая как и в предыдущем примере, мы получаем, что Она, играя "Ф", получает 1×р + 0×(1 - р), а играя "Б", получает 0×р+2×(1 - р). Следовательно 2×(1 - р) = р. Отсюда З×р = 2, а следовательно р = 2/3. Аналогично получаем 2q + (1 - q)×0 = 0×q + (l - q)×l, а значит 3q = 1 и q = 1/3. Таким образом, в смешанном равновесии Он играет "Ф" с вероятностью 2/3, а Она играет "Ф" с вероятностью 1/3.

Замечание 1.7.1. В определении смешанного расширения или равновесия в смешанных стратегиях мы предполагаем, что игроки осуществляют рандомизацию своих чистых стратегий независимо. Иными словами, мы можем считать, например, что Природа передает игрокам индивидуальные, независимо распределенные сигналы (q1, q2, …, qn) Î [0,1]x [0,1]x...x[0,1], а каждый игрок i принимает решение в зависимости от различных возможных реализаций его сигнала qi.

Предположим, однако, что есть некий общий сигнал qÎ[0,1], который могут наблюдать все игроки. В этом случае появляются новые возможности. Так, к примеру, в упомянутой только что игре "Семейный спор" оба игрока могут, например, решить идти на футбол, если, скажем, q< 1/2, и идти на балет, если q ³1/2. Выбор стратегии каждым игроком остается случайным, тем не менее здесь мы имеем дело со вполне скоординированными действиями (Он и Она оказываются вместе), явно имеющими равновесный характер, причем если один игрок решает следовать этому правилу, то и для второго оптимально придерживаться этого же правила. Это дает нам пример коррелированного равновесия (совместного равновесия)[13], введенного Р.Ауманом (Auman (1974)).

Формально такое равновесие — это специальный случай равновесия по Байесу-Нэшу, которое мы рассмотрим в главе 3.

Далее мы приведем важные результаты о существовании равновесий по Нэшу.

Предложение 1.7.2 В смешанном расширении 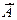любой игры Г с конечными множествами стратегий S₁,..., S_n существует равновесие по Нэшу в смешанных стратегиях.

Это предложение непосредственно следует из следующего более общего результата, так как в игре 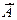множества стратегий игроков — это симплексы в соответствующем пространстве R^M.

Теорема 1.7.1 Debreu (1952), Glicksberg (1952), Fan Ky (1952)[14]. Если для каждого i = 1,..., п

(1) S_i — непусто, выпукло и компактно (в некотором R^M );

(2) u_i(s₁,..., s_n) — непрерывна по (s;,..., s_n) и квазивогнута по s;,

то в игре Г = {I, {S_i}, {u_i}} существует равновесие по Нэшу в чистых стратегиях.

Напомним, что функция f: R^K ® R называется квазивогнутой, если для любого а множество {х: f(x) ³ а} — выпукло.

Доказательство этого предложения опирается на следующую лемму.

Лемма 1.7.1 Если выполнены условия Теоремы 1.7.1, то отображение лучших ответов b_i непусто, выпуклозначно (т. е. множества b_i(s_-i) — непусты и выпуклы) и полунепрерывно сверху [15].

Доказательство леммы 1.7.1. Во-первых заметим, что b_i(s_-i) — это множество тех стратегий i-го игрока, которые максимизируют ui(×,s_-i) на компакте Si. Его непустота следует из непрерывности Ui. Выпуклость мно­жества bi(s-i) следует из квазивогнутости функции ui(-,s_;). Чтобы проверить полунепрерывность сверху, мы должны показать, что для любой последовательно­сти: (sf,s^) — > (s;,s_;), такой что sf G bi(s^_i)\/k мы имеем Si G 6(s_;). За­метим, что VA; Ui(s^s^) > Ui(s',s^) V s' G Si. В силу непрерывности u;(-), u₄(s₄,s_₄) > u₄(s',s_₄).

Доказательство Теоремы. Определим отображение b: S — > S формулой

6(si,..., s_n) = 6i(s_i) x 62(5-2) x • • • x b(s__n)

Ясно, что b(×) — многозначное отображение S = Si X • • • X S_n в себя. По лемме b(×) непусто, выпукло-значно, полунепрерывно сверху. Следовательно, по Т. Какутани о неподвижной точке существует неподвижная точка, т. е. набор стратегий s G S: s G b(s). Этот набор стратегий является равновесием по Нэшу, т.к. по построению

Si G bi(s-i) V г = 1,..., п. Справедлива также следующая теорема.

Теорема 1.7.2 (Glicksberg (1952)). Если в игре Г множества Si стратегий игроков являются непустыми компактными подмножествами метрического пространства, а функции выигрышей Ui непрерывны, то существует равновесие по Нэшу в смешанных стратегиях.

Пример. "Голосование". Рассмотрим следующую ситуацию — три игрока 1,2,3 и три альтернативы — А, D, С.

Игроки голосуют одновременно за одну из альтернатив, воздержаться невозможно. Таким образом, пространство стратегий Si = {А, В, С}. Альтернатива, получившая большинство, побеждает. Если ни одна из альтернатив не получает большинства, то выбирается альтернатива А. Функции выигрышей таковы:

u₁(А) = и₂(В) = и₃(с) = 2,

u₁(B) = и₂(С) = и₃(А) = 1,

u₁(С) = и₂(А) = и₃(В) = 0.

В этой игре три равновесных исхода[16] (в чистых стратегиях): А, В и С. Теперь посмотрим на равновесия (их больше 3): если игроки 1 и 3 голосуют за А, то игрок 2 не изменит исход, как бы он ни голосовал, и игроку 3 безразлично, как он голосует. (А, А, А) и (А, В, А) —р.Н., но (А, А, В) —не р.Н., т.к. второму лучше голосовать за В.

1.8 Модель дуополии по Курно

Предположим, что две фирмы i = 1,2 производят однородный продукт и q₁, q₂ — объемы производства этого продукта. Обратная функция спроса имеет вид (для простоты) P(Q) = а - Q, где Q = q₁ + q₂, (P(Q) = а - Q, при Q < а, и P(Q) = 0, при Q ³ а). Функции затрат C_i(q_i) = c×q_i (с < а) (нет фиксированных затрат и предельные затраты постоянны).

Фирмы выбирают q_i одновременно и независимо. Здесь два игрока, стратегии S_i = [0, +¥). (В действительности ни одна фирма не будет производить q_i > a). Фирмы максимизируют свои прибыли:

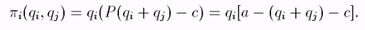
Если пара (q^*₁, q*₂) —р.Н., то q* решает задачу

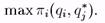
Предположим q* < а - с (можно доказать, что это действительно так), тогда условие 1 порядка[17] дает нам q_i = (а - q*_j - с)/2. Тогда

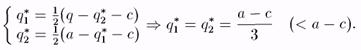
Заметим, что монопольный выпуск был бы (а - с)/2.

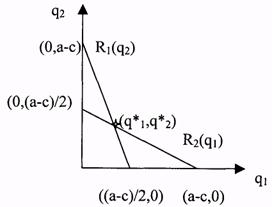
При исследовании дуополии по Курно важную роль играют функции лучших ответов (кривые реагирования) — это функции вида

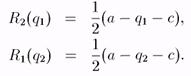
Таким образом, R_i(q_j) — это объем выпуска i-ой фирмы, максимизирующий ее прибыль при условии, что j-ая фирма производит q_j. Кривые реагирования изображены на рис. 23.

Точка пересечения кривых реагирования определяет равновесие по Курно, т. е. равновесие по Нэшу в модели дуополии по Курно.

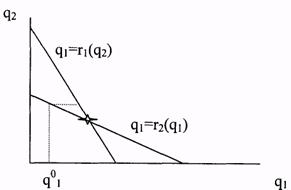
Рис. 24.

1.9 Равновесие по Нэшу в дуополии по Курно как результат обучения

Мы будем предполагать сейчас, что игроки пытаются предсказывать игру своих оппонентов, "используя свой предыдущий опыт". Эта идея восходит еще к Курно, который рассматривал своеобразный динамический вариант нахождения равновесия. При этом игроки выбирали объем выпуска по очереди, как лучший ответ, исходя из выбора оппонента на предыдущем шаге, предполагая ("гипотеза Курно"), что он (оппонент) оставит свой объем выпуска без изменения.

Точнее, если игрок 1 делает ход в период 0 и выбирает q⁰₁ то выпуск игрока 2 в период 1 есть q¹₂ = r2(q⁰₁), где r2(q⁰₁) — функция реагирования второго игрока. Затем

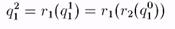
Если этот процесс сходится к (q*₁, q*₂), то q*₂ = r₂(q*₁) и q*₁ = r₁(q*₂), т.е. (q*₁, q*₂) — р.Н. Если процесс сходится к некоторому состоянию 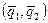для любого начального состояния, достаточно близкого к нему, то говорят, что состояние (q*₁, q*₂) — асимптотически устойчиво, а сам процесс называется процессом нащупывания (см. рис.24)[18].

Дата добавления: 2014-10-31