Элементы теории кооперативных игр 183 4 страница

В общем случае картина может быть более сложной (см. рис.25): С, Е, G — неустойчивы (к ним процесс не сходится, если только не начинается в них самих), В, D и F — устойчивы.

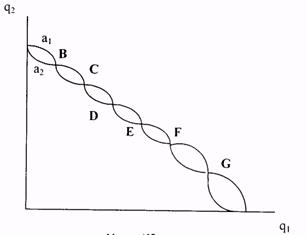
Рис. 25.

Вообще говоря, достаточное условие устойчивости выглядит следующим образом:

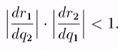
Заметим, что если функции выигрышей дважды непрерывно дифференцируемы, тс наклон функции реагирования i-ой фирмы есть

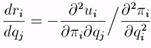
1.10 Дуополия по Бертрану

1. Парадокс Бертрана. Рассмотрим теперь ситуацию, когда две фирмы (как в дуополии по Курно) производят однородный продукт, но теперь мы предположим, что фирмы одновременно и независимо объявляют цену, по которой они готовы продавать свою продукцию. Тогда спрос, с которым сталкивается каждая фирма, определяется следующим образом:

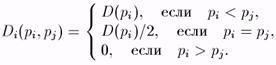
Иными словами, фирма, назначившая меньшую цену "получает" весь спрос, а если цены одинаковы, то потребители покупают продукцию фирм равновероятно.

Предположим, что цены (p*₁, p*₂) образуют равновесие по Нэшу. Во-первых, очевидно, что р*_i ³ с, так как назначение цены ниже предельных затрат приведет к отрицательной прибыли, чего не может быть в равновесии, т.к. цена, равная предельным затратам, обеспечивает нулевую прибыль. Далее, ни одна из цен р*_i не может быть выше с. Действительно, предположим для определенности, что р*₁ > с, тогда если p*₂³p*₁, то фирма 2, сталкивающаяся в этом варианте в лучшем случае с половинным спросом, может "перехватить" весь спрос, назначив цену р'₂ = р*₁-e для достаточно малого e> 0 и тем самым улучшив свое положение. Если же р*₁ > р*₂ > с, то фирма 1, аналогично, может назначить цену р*₂ -e, "перехватывая" весь спрос.

Таким образом, в равновесии по Бертрану (или в равновесии по Нэшу в дуополии по Бертрану p*₁ = p*₂ = с, и фирмы получают нулевую прибыль. Это и есть пар доке Бертрана.

Как можно избежать этой парадоксальной ситуации? Во-первых, можно ввести условие ограничения мощности фирм, то есть считать, что есть цены, при которых фирмы не могут обеспечить весь спрос. Во-вторых, можно снять условие однократности этой игры, и это, как мы увидим позднее в гл. 2, существенно меняет ситуацию. Наконец, можно избавиться от предположения об однородности продукции.

2. Рассмотрим ситуацию с дифференцируемыми продуктами. Фирмы 1 и 2 выбирают цены p₁ и р₂ одновременно и независимо. Спрос, с которым сталкивается фирма i, q_i(p_i, p_j) = a - p_i + b×p_j, где b > 0 — отражает степень заменяемости i-ого продукта j-ым. (Мы не обсуждаем здесь реалистичность такой функции спроса). Предельные затраты есть с, с < а. Пространство стратегий — это Si = [0, ¥) — фирмы выбирают цены. Тогда прибыль i-ой фирмы определяется равенством

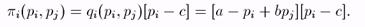
Пара (p*₁, p*₂) образует р.Н., если для " i р*_i решает задачу

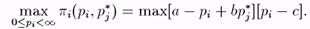
Решение задачи для i-ой фирмы есть

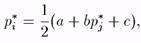
то есть

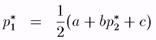
Следовательно, p*₁ = p*₂= (а + с)/(2 - b)

1.11 Пример "Проблема общего'

Рассмотрим следующую очень стилизованную модель (Hardin (1968)). Представим себе, что есть n фермеров. Летом их козы (коровы) пасутся на зеленом поле. Обозначим через g_i — число коз у i-ого фермера, тогда численность всего стада — G = g₁ + … + g_n. Затраты на покупку и содержание козы равны с (независимо от числа коз у фермера). Ценность (стоимость) одной козы при общем числе коз G есть v(G).

Предполагая, что козе необходим определенный уровень минимального пропитания (для выживания), считаем, что есть некоторое максимальное число коз, которое может прокормиться, G_max: v(G) > 0 для G < G_max, но v(G) = 0 для G > G_max. Можно предположить, что если есть одна коза, то она спокойно прокормится; можно добавить еще одну и т.д., но с ростом числа коз, естественно считать, что ценность падает v'(G)<0, (G<G_max) и v"(G)<0.

Весной фермеры выбирают (одновременно и независимо), сколько заводить коз (g_i для i-ого фермера). Выигрыш фермера i есть

(*)

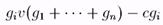Следовательно, если (g*₁,..., g*_n) — р. Н., то g*_i должно максимизировать (*) при (g*₁,..., g*_i-1, g*_i+1, …, g*_n) • Условие 1 порядка есть

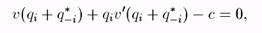
где

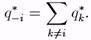
Подставим в это равенство g*_i и, просуммировав по i, получаем (разделив на n)

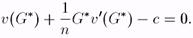
Рассмотрим теперь, что произойдет, если "социальный плановик" будет искать социальный оптимум, то есть решать задачу нахождения

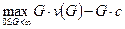
Здесь условие 1-го порядка есть:

v(G**) + G**v'(G**) - с = 0.

Нетрудно проверить, что G* > G***, т. е. слишком много коз! Иными словами, общие ресурсы используются слишком интенсивно.

1.12 Равновесие "дрожащей руки

Мы уже обсуждали ранее слабо доминируемые стратегии и сейчас вновь обратимся к ним. Рассмотрим игру, изображенную на рис. 26.

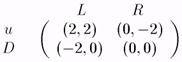
Рис. 26.

Легко видеть, что в этой игре два р.Н. в чистых стратегиях (u, L) и (D, R), причем второе равновесие характерно тем, что оба игрока выбирают свои слабо доминируемые стратегии.

Мы остановимся сейчас на определении совершенного равновесия (по Нэшу) дрожащей руки игры в нормальной форме[19], определение которого восходит к работе Рейнхарда Зельтена[20] Selten (1975). Такое равновесие "выдерживает" возможность того, что с некоторой очень небольшой вероятностью игроки делают ошибки (грубо говоря, "дрожащей рукой" не попадая на нужные кнопки).

Для произвольной игры в нормальной форме Г = {I, (S_i),(u_i)} можно определить "возмущенную" игру Г_e = {I, (S^e_i), (u_i)}, выбирая для каждого игрока i и каждой чистой стратегии s_i Î S_i числа e_i(s_i) Î (0,1) так, что 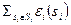< 1, и затем, определяя множество "возмущенных" стратегий как

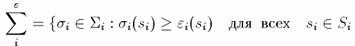
и

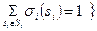
Иными словами, в игре Г_e каждый игрок i играет каждую свою стратегию s_i с вероятностью не меньшей чем некоторая минимальная вероятность e_i(s_i), которая интерпретируется как неизбежная вероятность сыграть s_i по ошибке.

Определение 1.12.1 Равновесие по Нэшу s в игре (в нормальной форме) Г = {I, (S_i),(u_i) } называется равновесием дрожащей руки, если существует такая последовательность возмущенных игр 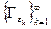_; сходящихся к Г (в том смысле, что 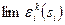= 0 для любых iÎI и s_iÎ S_i), что существует последовательность равновесий (в соответствующих играх Г_ek) 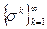, сходящаяся к s, т.е 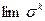= s.

Таким образом, рассматриваемые равновесия — это те равновесия по Нэшу, которые "выживают" при возможных ошибках.

Заметим, что в определении требуется лишь существование возмущенных игр, имеющих равновесия, близкие к s. Более сильным было бы требование "выживания" при всех возмущениях исходной игры.

Предложение 1.12.1 (Selten 1975). В смешанном расширении любой игры Г = {I, (S_i),(u_i) } с конечными множествами стратегий S₁,..., S_n существует равновесие дрожащей руки.

Предложение 1.12.2 (Selten (1975)). Равновесие по Нэшу а в игре в нормальной форме Г = {/, (S^, (ui)} является совершенным равновесием дрожащей руки (в игре в нормальной форме) тогда и только тогда, когда существует последо­вательность таких вполне смешанных стратегий a^k (т. е. стратегий, в кото­рых все чистые стратегии играются с положительными вероятностями), что a^k — Y а и <Ji является лучшим ответом на любой элемент последовательности {сг^}^_₁ для любого г = 1,..., п.

Предложение 1.12.3 (Selten (1975)). Если а = (<т;,..., <т_п) — совершенное рав­новесие дрожащей руки (в игре в нормальной форме), то <т; не является слабо доминируемой ни для какого i = 1,..., п.

1.13 Дополнение: Антагонистические игры

К числу достаточно простых и потому наиболее изученных игр относятся антагонистические игры. В случае антагонистических игр, в отличие от произвольных игр, можно достаточно много сказать о качественном характере равновесий по Нэшу. Напомним определение игр с "нулевой суммой".

Определение 1.13.1 Игра Г = {I, (S_i),(u_i) } называется игрой с нулевой суммой, если для любого sÎS выполняется условие .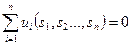

Иными словами, такая игра представляет собой замкнутую систему: все то, что кто-нибудь выиграл, должно быть кем-то проиграно. Большинство салонных игр являются играми такого типа.

Будем далее считать, что I = {1,2}.

Определение 1.13.2 Игра Г двух лиц с нулевой суммой называется антагонстической.

В такой игре интересы игроков диаметрально противоположны, поскольку u1(s1, s2) + u2(si, s2) = 0 или u1(si,s2) = -u2(si, s2), для "s1ÎS1, s2ÎS2. К числу примеров антагонистических игр можно отнести игру "Орел или Решка". В этой игре каждый из двух игроков выбирает, независимо от другого, монетку, поверну­тую вверх либо "Орлом", либо "Решкой". Если выбор игроков различен, то игрок 1 платит игроку 2 один доллар. Если выбор совпадает, то — наоборот. Матрица выигрышей такой игры представлена на Рис. 27.

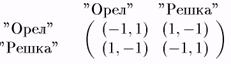
Рис. 27.

Как уже отмечалось, конечная антагонистическая игра называется матричной.

Будем говорить, что игрок i выбирает максиминную стратегию, если эта стратегия является наилучшей для него в предположении, что игрок j будет выбирать свою стратегию так, чтобы максимально навредить игроку i.

Рассмотрим такую стратегию на примере игры, представленной на рис. 28.

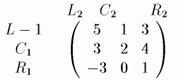
Рис. 28.

Здесь приведена матрица выигрышей 1-го игрока. Как выбирает максиминную стратегию 1-ый игрок? Он может рассуждать следующим образом: "Если я выберу свою стратегию L1, то сколько я смогу получить?" Поскольку его противник выбирает свою стратегию так, чтобы навредить игроку 1 насколько возможно, то он в ответ на L1 ответит своей стратегией С2 - В этом случае игрок 2 проиграет лишь 1. Аналогично, если игрок 1 задумает сыграть С1, в ответ игрок 2 ответит С2, тогда 1-ый игрок сможет выиграть лишь 2. Если же игрок 1 задумает сыграть R1, то противник накажет его, сыграв L2. В этом случае 1 игрок проиграет 3, а следовательно, 2-ой игрок выиграет 3. Очевидно, что для игрока 1, наилучшим будет выбор такой стратегии, которая даст ему максимальный выигрыш из тех минимальных, которые позволит ему выиграть игрок 2, т. е. стратегии С1.

Аналогичные рассуждения применимы и для игрока 2 при выборе им своей максиминной стратегии.

Покажем, что если в антагонистической игре Г существует равновесие по Нэшу, то пара стратегий будет являться равновесной тогда и только тогда, когда стратегия каждого игрока — максиминная. Этот в некотором смысле удивительный результат обеспечивает связь между индивидуальным принятием решения и рассуждением, объясняющим причину введения такого понятия как равновесия по Нэшу. Мы докажем заодно, что все равновесные ситуации в антагонистических играх приводят к одним и тем же выигрышам. Это свойство редко выполняется в неантагонистических играх.

Определение 1.13.3 Пусть Г - антагонистическая игра. Стратегия s*₁ÎS₁ является максиминной для игрока 1, если

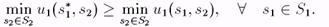
Стратегия s*₂ÎS₂ является максиминной для игрока 2, если

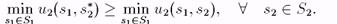
Т. е. максиминная стратегия для игрока i является стратегией, обеспечивающей ему максимальный гарантированный выигрыш. Следовательно, максиминная стратегия игрока 1 решает задачу:

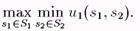
Аналогично максиминная стратегия 2-го игрока решает задачу:

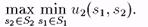
Следующая очевидная лемма показывает, что нахождение максимального среди минимальных выигрышей игрока 2 эквивалентно нахождению минимума среди максимальных выигрышей игрока 1.

Лемма 1.13.1 Пусть Г = {{1,2}, {S_i}, {u_i}} — антагонистическая игра, тогда

Доказательство этой леммы немедленно следует из следующих очевидных свойств:

1) ;

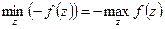2)

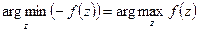
Из этого результата следует, что стратегия s₂ÎS₂ является решением задачи нахождения 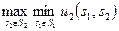, тогда и только тогда, когда эта стратегия s₂ является решением задачи 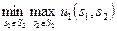. Поэтому при поиске такой стратегии можно воспользоваться той же матрицей выигрышей игрока 1 следующим образом: сначала в каждом столбце найти максимальный элемент, затем из всех максимальных элементов выбрать минимальный. Полученное значение является "наименьшим гарантированным проигрышем" игрока 2. Это означает, что если игрок 2 будет придерживаться стратегий, соответствующих этому минимаксному значению, то при любом поведении противника он проиграет не больше этого значения.

Следующий результат устанавливает связь между равновесием по Нэшу в антагонистической игре и множеством пар максиминных стратегий.

Предложение 1.13.1 Пусть Г — антагонистическая игра.

a. Если (s*₁, s*₂) — равновесие по Нэшу в Г, тогда s*₁ - является максиминной стратегией игрока 1, a s* - является максиминной стратегией игрока 2.

b. Если (s*₁, s*₂) — равновесие по Нэшу в игре Г, тогда

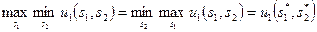
и таким образом все равновесия по Нэшу в игре Г дают одни и те же выигрыши.

c. Если

,

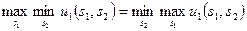s*₁ — является максиминной стратегией игрока 1, s*₂ — является максиминной стратегией игрока 2, тогда (s*₁, s*₂) является равновесием по Нэшу игры Г.

Доказательство.

а,b. Пусть s*₁, s*₂) - равновесие по Нэшу, тогда

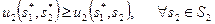
Или (т.к. u₂ = -u₁)

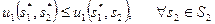
Следовательно,

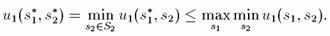(8.1)

С другой стороны,

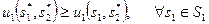
Следовательно,

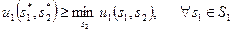
поэтому

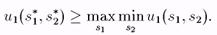
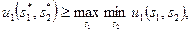(8.2)

Таким образом, из (1) и (2) следует, что u^s^s^) = max_si min_S2 Ui(si, s₂) и является максиминной стратегией игрока 1. Аналогично можно показать, что является максиминной стратегией игрока 2.

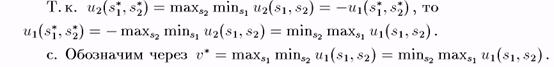
Из леммы

следует, что max_S2 min_si u₂(si,s₂) = —v*. Поскольку Sj — максиминная стратегия 1-ого игрока, то Ui(sj,s₂) > v* для всех s₂ Е 82 - Аналогично, s^ — максиминная стратегия 2-ого игрока, поэтому

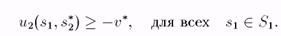
Положим в этих неравенствах s₂ = s% и Si = Sj, тогда Ui^j,^) > и* и u₂(sj,S2) > —и*. Но так как и\ = — и₂, то u^Sj,^) < и*. Отсюда следует, что ui^i,^) = v*. Получим Ui(sj,s₂) > u₂(sj,S2) или, подставляя ui = —u₂ имеем, u₂(sj,S2) > ^2(5i,s₂). А из второго неравенства ^(si,^) ^ ~^ui(^si?^s2) ^или Ui(sj,S2) > «1(51,52). Значит пара (sj,^^) является равновесием по Нэшу.

Заметим также, что из свойств (а), (с) следует, что равновесные стратегии являются взаимозаменяемыми в том смысле, что если (si, s₂) и (s'j, s₂) образуют равновесия, то и (si,s₂), (sj,s₂) — также образуют равновесия по Нэшу.

Свойство (b) показывает, что

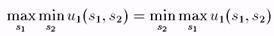
для всех антагонистических игр, в которых существует равновесие по Нэшу.

В более общем случае, когда равновесия по Нэшу в чистых стратегиях нет, выполняется более общее свойство:

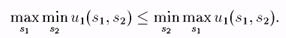
Действительно, т. к. для любого s\ имеем

поэтому

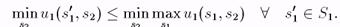
Наличие равновесной ситуации предполагает выполнение противоположного неравенства. В примере "Орел или Решка" мы видим, что

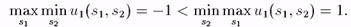
Значит в этой игре равновесия по Нэшу в чистых стратегиях не имеет, а вот во втором примере мы получаем, что

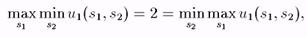
когда игрок 1 играет С\, а игрок 2 играет С2 - Ситуация (С\,Съ) здесь является равновесной по Нэшу.

Если оказывается, что в антагонистической игре Г

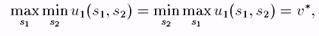
то говорят, что этот равновесный выигрыш 1-ого игрока является значением игры. И как следует из доказательства предложения, если v* является значением антагонистической игры, то это значит, что любая равновесная стратегия игрока 1 гарантирует ему выигрыш по крайней мере не меньше его равновесного выигрыша v*, a любая равновесная стратегия игрока 2 гарантирует ему не меньше его равновесного выигрыша — v*.

Поэтому любая такая стратегия игрока 2 гарантирует, что игрок 1 получит выигрыш не больше его равновесного. В неантагонистических играх равновесные стратегии игроков такими свойствами уже не обладают.

1.14 Дополнение. Решение биматричных игр 2x2

В этом параграфе мы подробно остановимся на анализе решений биматричных игр, в которых у каждого из игроков есть только две стратегии. Разумеется, эти игры представляют собой частный случай рассмотренных ранее игр, но здесь появляется возможность дать наглядную графическую интерпретацию поиска равновесных ситуаций в игре. (Наше изложение здесь следует книге Воробьева (1985).) Рассмотрим биматричную игру 2x2 с матрицей

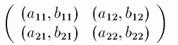
или, как мы уже отмечали, игру, выигрыши в которой можно задать с помощью двух матриц:

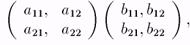
первая из которых описывает выигрыши игрока 1, а вторая — выигрыши второго.

Очевидно, что смешанные стратегии игроков в случае игр 2x2 полностью описываются вероятностями р и q выбора игроками своих первых чистых стратегий. (Вторые чистые стратегии выбираются, соответственно, с вероятностями 1 — р и 1 — q.) Поэтому, поскольку 0 < р, q < 1, каждая ситуация в смешанных стратегиях в биматричной игре 2x2 представляется как точка на единичном квадрате.

Напомним, что пара смешанных стратегий s*₁ = (р*, 1 - р*)и

s*₂ = (q*, 1 - q*)является равновесием по Нэшу, если смешанная стратегия s*_i одного игрока является лучшим ответом на смешанную стратегию s*_jдругого игрока, т. е. выполняются следующие неравенства:

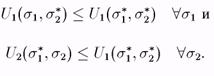
Рассмотрим уже знакомый нам пример "Орел или Решка". Пусть игрок 1 считает, что игрок 2 будет выбирать "Орла" с вероятностью q и "Решку" с вероятностью 1 - q. Ожидаемый выигрыш игрока 1 от разыгрывания "Орла" будет (-1)q + 1•(1 - q) = 1 - 2q, а от разыгрывания "Решки" 1•q + (- 1)•1 - q) = 2q-1. Если 1 - 2q > 2q-1, т. е. q < 1/2, то лучшей чистой стратегией игрока 1 будет Орел, а если q > 1/2, то Решка, и игроку 1 будет все равно, что разыгрывать, если q = 1/2. Рассмотрим возможные смешанные стратегии игрока 1. Пусть (р, 1 — р) обозначает смешанную стратегию, в которой игрок 1 разыгрывает "Орла" с вероятностью р. Для каждого значения q мы можем вычислить значения р = p*(q), такие что, (р, 1 - р) будет являться лучшим ответом игрока 1 на (q, 1 - q) игрока 2.

Ожидаемый выигрыш игрока 1 от разыгрывания (р, 1 - р), когда игрок 2 разыгрывает (q, 1 - q)будет

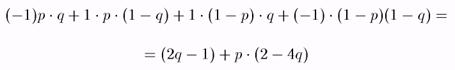
Ожидаемый выигрыш игрока 1 повышается (в зависимости от р), если 2 - 4q > 0 и уменьшается, если 2 - 4q < 0, поэтому лучший ответ игрока 1 (среди всех стратегий, как чистых, так и смешанных), есть р = 1 (т.е. Орел), если q < ½,

но р = 0 (т.е. Решка), если q > 1/2, Этим значениям р соответствуют два горизонтальных отрезка на рис. 29.

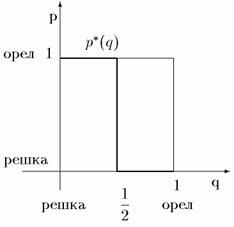
рис. 29.

Так как при q = 1/2 ожидаемый выигрыш игрока 1 не зависит от его стратегии, мы получаем, что игроку 1 безразлично, выбрать ли одну из своих чистых стратегий, или же выбрать какую-нибудь смешанную стратегию (р, 1 - р). Это означает, что если q = 1/2, то смешанная стратегия (р, 1 - р) является лучшим ответом на смешанную стратегию (q, 1 - q) при любом значении р от 0 до 1. Поэтому p*(1/2) представляет собой вертикальный отрезок, изображенный на рис.29. Таким образом, ломаная линия на рис. 29 представляет собой многозначное отображение (поскольку при q = 1/2 мы имеем целый отрезок) лучших ответов (в зависимости от q).

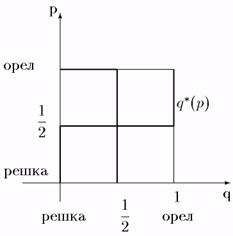
рис. 30.

Похожими рассуждениями и в силу симметрии матрицы выигрышей игрока 2 получаем аналогичное отображение лучших ответов игрока 2. На рис. 30 это ломаная q*(р). Рис. 30 показывает, что равновесие по Нэшу в игре "Орел или Решка" возникает, если игрок 1 разыгрывает смешанную стратегию (1/2, 1/2) и игрок 2 разыгрывает такую же стратегию, что, по-видимому, было естественно ожидать в силу симметричности игры. Важно заметить, что этот пример иллюстрирует, что неслучайно, если один из игроков выбирает свои стратегии равновероятно (т. е. придерживается своей равновесной стратегии), то второму игроку при этом абсолютно безразлично как играть. Это следует из свойства, доказанного ранее (см. п.1.7) в общем случае:

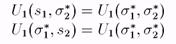(1)

которые входят в равновесную ситуацию с ненулевыми вероятностями. Для тех же s'_i, которые входят в равновесную ситуацию с нулевой вероятностью верны неравенства:

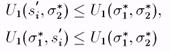(2)

Формулы (1), (2) дают действенный способ определения равновесных ситуаций в произвольных биматричных играх 2x2.

Ожидаемый выигрыш игрока 1 от разыгрывания s₁ = (р, 1 - р), когда игрок 2 разыгрывает s₂ = (q, 1 - q):

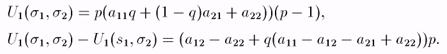
Введем обозначения: С = а₁₁ - а₁₂ - a₂₁ + a₂₂, a = a₂₂ - a₁₂. Лучший ответ игрока 1 на произвольную стратегию s₂ игрока 2 можно получить из условий неотрицательности:

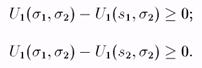
С учетом введенных обозначений они выглядят следующим образом:

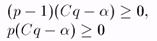(3)

Аналогично можно поступить для нахождения лучшего ответа игрока 2. Ожидаемый выигрыш игрока 2 от игры s₂ = (q, 1 - q), когда игрок 1 играет s₁ = (р, 1 - р):

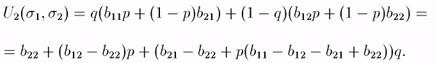
Из условий (неотрицательности)

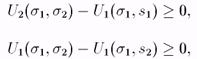
обозначив D = b₁₁ - b ₁₂ - b ₂₁ + b₂₂, b = b₂₂ - b₂₁, получаем аналогичные неравенства для нахождения лучшего ответа игрока 2 на произвольную стратегию а = (р, 1 - р) игрока 1:

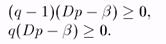(4)

Тогда, для того чтобы пара s₁ = (р, 1 - р), s₂ = (q, 1 - q) определяла равновесную ситуацию необходимо и достаточно одновременное выполнение систем неравенств (3), (4), а также 0 £ р £ 1, 0 £ q £ 1.

Рассмотрим лучшие ответы каждого игрока, которые, разумеется, зависят от того, как устроены матрицы выигрышей игрока 1 и игрока 2. Начнем с неравенств (3).

Возможны три случая:

1) р=1, Cq ³ a;

2) 0 <р< 1, Cq = a; (5)

3)р = 0, С×q £ a.

В свою очередь, в зависимости от соотношений между С и a, возможны следующие случаи и соответствующие лучшие ответы игрока 1 в каждом из них.

I. Если С > 0, a > 0, то лучшие ответы изображены на рис. 31-33:

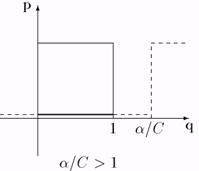
рис. 31.

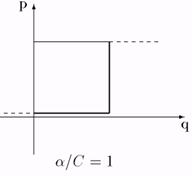
рис. 32.

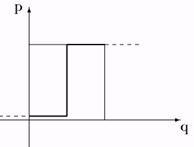
a/С < 1

рис. 33.

II. Если С < 0, а < 0, то лучшие ответы изображены на рис. 34-36:

Дата добавления: 2014-10-31