Геометрична інтерпретація ЗЛП

ФОРМИ ЗАПИСУ ЗАДАЧ ЛП

Задачу ЛП (ЗЛП) зручно записувати за допомогою знака суми «S». Справді, задачу (4)—(6) можна подати так:

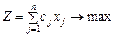
за умов

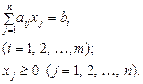
Ще компактнішим є запис ЗЛП у векторно-матричному вигляді:

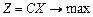
за умов

АХ = А ₀,

Х 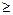0,

де

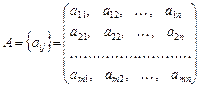
є матриця коефіцієнтів при змінних;

— вектор змінних; 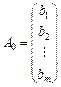— вектор вільних членів;

С = (с ₁, с ₂, …, с_п) — вектор коефіцієнтів при змінних у цільовій функції.

Часто ЗЛП зручно записувати у векторній формі:

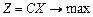
за умов

,

,

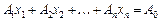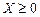де

, , …,

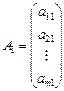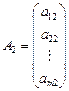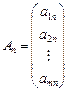
є вектори коефіцієнтів при змінних.

Геометричну інтерпретацію ЗЛП розглянемо на такому прикладі. Нехай фермер прийняв рішення вирощувати озиму пшеницю і цукровий буряк на площі 20 га, відвівши під цукровий буряк не менш як 5 га. Техніко-економічні показники вирощування цих культур наведені в таблиці:

№ п/п	Техніко-економічний показник із розрахунку на 1 га	Сільськогосподарська культура	Наявний ресурс
Озима пшениця	Цукровий буряк
	Жива праця, людино-днів
	Механізована праця, людино-днів
	Прибуток, тис. грн.	0,7

Критерієм оптимальності є максимізація прибутку.

Запишемо економіко-математичну модель структури виробництва озимої пшениці та цукрового буряка, скориставшись такими позначеннями:

х ₁ — шукана площа посіву озимої пшениці;

х ₂ — шукана площа посіву цукрового буряка.

ЗЛП має вигляд:

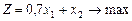(7)

за умов

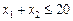, (8)

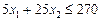, (9)

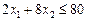, (10)

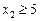, (11)

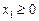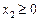, . (12)

Геометричну інтерпретацію задачі наведено на рис. 1.

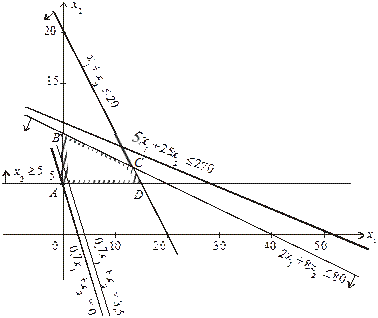
Рис. 1. Область допустимих розв’язків

Область допустимих розв’язків дістаємо так. Кожне обмеження, наприклад х ₁ + х ₂ ≤ 20, задає півплощину з граничною прямою х ₁ + х ₂ = 20. Будуємо її і визначаємо півплощину, яка описується нерівністю х ₁ + х ₂ ≤ 20. З цією метою в нерівність х ₁ + х ₂ ≤ 20 підставляємо координати якоїсь характерної точки, скажімо х ₁ = 0 і х ₂ = 0. Переконуємося, що ця точка належить півплощині х ₁ + х ₂ ≤ 20. Цей факт на рис. 2.1 ілюструємо відповідною напрямленою стрілкою. Аналогічно будуємо півплощини, які відповідають нерівностям (8)—(12). У результаті перетину цих півплощин утворюється область допустимих розв’язків задачі (на рис. 2.1 — многокутник ABCD). Цільова функція 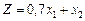описує сім’ю паралельних прямих, кожна з яких відповідає певному значенню Z. Зокрема, якщо Z = 0, маємо 0,7 х ₁ + х ₂ = 0. Ця пряма проходить через початок системи координат. Коли Z = 3,5, дістаємо пряму 0,7 х ₁ + х ₂ = 3,5.

Загальна задача лінійного програмування (1)—(3) геометрично інтерпретується так: кожне і -те обмеження, що має вигляд рівняння

,

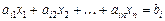у п -вимірному просторі основних змінних х ₁, х ₂, …, х_п задає гіперплощину. Кожному обмеженню виду (2) і (3) відповідають гіперплощина та півпростір, який лежить по один бік цієї гіперплощини. У перетині всіх півпросторів, що визначаються обмеженнями задачі (2) і (3), утворюється опуклий многогранник допустимих її розв’язків.

Цільову функцію

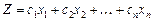
в п -вимірному просторі основних змінних можна геометрично інтерпретувати як сім’ю паралельних гіперплощин, положення кожної з яких визначається значенням параметра Z.

Дата добавления: 2014-10-31