Теоретичні відомості

Алгоритм рішення задачі симплексним методом

Теоретичні відомості

План

Графічний метод для визначення оптимального плану задачі лінійного програмування доцільно застосовувати лише для задач із двома змінними. За більшої кількості змінних вдаються до загального методу розв’язування задач лінійного програмування — так званого симплекс-методу. Процес розв’язування задачі симплекс-методом має ітераційний характер: обчислювальні процедури (ітерації) одного й того самого типу повторюються у певній послідовності доти, доки не буде отримано оптимальний план задачі або з’ясовано, що його не існує.

Отже, симплекс-метод — це поетапна обчислювальна процедура, в основу якої покладено принцип послідовного поліпшення значень цільової функції переходом від одного опорного плану задачі лінійного програмування до іншого.

Алгоритм розв’язування задачі лінійного програмування симплекс-методом складається з п’яти етапів:

1. Визначення початкового опорного плану задачі лінійного програмування.

2. Побудова симплексної таблиці.

3. Перевірка опорного плану на оптимальність за допомогою оцінок Z_j – C_j. Якщо всі оцінки задовольняють умову оптимальності, то визначений опорний план є оптимальним планом задачі. Якщо хоча б одна з оцінок Z_j – C_j не задовольняє умову оптимальності, то переходять до нового опорного плану або встановлюють, що оптимального плану задачі не існує.

4. Перехід до нового опорного плану задачі виконується визначенням розв’язувального елемента та розрахунком нової симплексної таблиці.

5. Повторення дій починаючи з п. 3.

Розглянемо докладніше кожний з етапів алгоритму.

1. Визначення першого опорного плану починають із запису задачі лінійного програмування в канонічній формі, тобто у вигляді обмежень-рівнянь з невід’ємними правими частинами. Якщо в умові задачі присутні обмеження-нерівності, то перетворення їх на рівняння виконується за допомогою додаткових змінних, які вводяться до лівої частини обмежень типу «≤» зі знаком «+», а до обмежень типу «≥» — зі знаком «–». У цільовій функції задачі додаткові змінні мають коефіцієнт нуль.

Після зведення задачі до канонічного вигляду її записують у векторній формі. За означенням опорного плану задачі лінійного програмування його утворюють т одиничних лінійно незалежних векторів, які становлять базис т -вимірного простору (де т — кількість обмежень у задачі лінійного програмування).

На цьому етапі розв’язування задачі можливі такі випадки:

· після запису задачі у векторній формі в системі обмежень є необхідна кількість одиничних векторів. Тоді початковий опорний план визначається безпосередньо без додаткових дій;

· у системі обмежень немає необхідної кількості одиничних незалежних векторів. Тоді для побудови першого опорного плану застосовують метод штучного базису. Ідея його полягає в тому, що відсутні одиничні вектори можна дістати, увівши до відповідних обмежень деякі змінні з коефіцієнтом +1, які називаються штучними. У цільовій функції задачі лінійного програмування штучні змінні мають коефіцієнт + М (для задачі на min) або – М (для задачі на max), де М — досить велике додатне число.

Визначені одиничні лінійно незалежні вектори утворюють базис, і змінні задачі, що відповідають їм, називають базисними, а всі інші змінні — вільними. Їх прирівнюють до нуля та з кожного обмеження задачі визначають значення базисних змінних. У такий спосіб отримують початковий опорний план задачі лінійного програмування.

2. Подальший обчислювальний процес та перевірку опорного плану на оптимальність подають у вигляді симплексної таблиці.

У першому стовпчику таблиці — «Базис» — записують базис­ні змінні опорного плану, причому в тій послідовності, в якій вони розміщуються в системі обмежень задачі.

Наступний стовпчик симплексної таблиці — «С _баз» — коефіцієнти при базисних змінних у цільовій функції задачі.

У третьому стовпчику — «План» — записують значення базис­них змінних і відшукувані у процесі розв’язування задачі компоненти оптимального плану.

У решті стовпчиків симплексної таблиці, кількість яких відповідає кількості змінних задачі, записують відповідні коефіцієнти з кожного обмеження задачі лінійного програмування.

3. Перевіряють опорний план на оптимальність згідно з наведеною далі теоремою.

Теорема (ознака оптимальності опорного плану). Опорний план задачі лінійного програмування є оптимальним, якщо для всіх 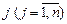виконується умова

(для задачі на max)

або

(для задачі на min)

Якщо для побудови опорного плану було використано метод штучного базису, необхідною умовою оптимальності є також вимога, щоб у процесі розв’язування задачі всі штучні змінні були виведені з базису і дорівнювали нулю.

Значення оцінок 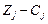визначають за формулою

або безпосередньо із симплексної таблиці як скалярний добуток векторів-стовпчиків «С _баз» та «x_j» мінус відповідний коефіцієнт С_j. Розраховані оцінки записують в окремий рядок симплексної таблиці, який називають оцінковим.

У процесі перевірки умови оптимальності можливі такі випадки:

а) усі 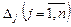задовольняють умову оптимальності, і тоді визначений опорний план є оптимальним;

б) не всі задовольняють умову оптимальності, і тоді потріб­но виконати перехід до наступного, нового опорного плану задачі.

4. Перехід від одного опорного плану до іншого виконується зміною базису, тобто виключенням з нього деякої змінної та введенням замість неї нової з числа вільних змінних задачі.

Змінна, яка включається до нового базису, відповідає тій оцін­ці 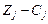, що не задовольняє умову оптимальності. Якщо таких оцінок кілька, серед них вибирають найбільшу за абсолютною величиною і відповідну їй змінну вводять до базису. Припустимо, що індекс зазначеної змінної j = k. Відповідний стовпчик симплексної таблиці називають напрямним.

Для визначення змінної, що має бути виключена з базису, знаходять для всіх додатних a_ik напрямного стовпчика величину . Вибирають найменше значення θ, яке вказує на змінну, що виводиться з базису. Припустимо, що це виконується для 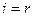. Відповідний рядок симплексної таблиці називатиметься напрямним.

Перетином напрямного стовпчика та напрямного рядка визначається число симплексної таблиці a_rk, яке називають розв’язувальним елементом. За допомогою елемента a_rk і методу Жордана—Гаусса розраховують нову симплексну таблицю.

Далі ітераційний процес повторюють доти, доки не буде визначено оптимальний план задачі.

У разі застосування симплекс-методу для розв’язування задач лінійного програмування можливі такі випадки.

1. Якщо в оцінковому рядку останньої симплексної таблиці оцінка Z_j – C_j = 0 відповідає вільній (небазисній) змінній, то це означає, що задача лінійного програмування має альтернативний оптимальний план. Отримати його можна, вибравши розв’язу­вальний елемент у зазначеному стовпчику таблиці та здійснивши один крок симплекс-методом.

2. Якщо при переході у симплекс-методі від одного опорного плану задачі до іншого в напрямному стовпчику немає додатних елементів a_ik, тобто неможливо вибрати змінну, яка має бути виведена з базису, то це означає, що цільова функція задачі лінійного програмування є необмеженою й оптимальних планів не існує.

3. Якщо для опорного плану задачі лінійного програмування всі оцінки задовольняють умову оптимальності, але при цьому хоча б одна штучна змінна є базисною і має додатне значення, то це означає, що система обмежень задачі несумісна й оптимальних планів такої задачі не існує.

Більш універсальним і основним методом рішення задач лінійного програмування є симплексний метод. Цей метод розроблений американським ученим Дж. Данцигом і був опублікований у 1947 році. Він дозволяє вирішити задачу з будь-яким числом шуканих невідомих. За допомогою симплексного методу з безлічі можливих можна вибрати єдине рішення, що у прийнятих умовах буде найкращим (оптимальним).

Симплексний метод дозволяє здійснити послідовний цілеспрямований підхід від одного припустимого плану до іншого. При цьому упорядкований перехід від менш вигідного варіанта до кращого забезпечує за кінцеве число кроків одержання оптимального варіанта. Кожний з цих кроків складається в перебуванні нового плану, якому відповідає більше чи менше значення цільової функції, чим значення цієї ж функції в попередньому плані. Процес повторюється доти, поки не буде отриманий оптимальний план, що має екстремальне значення.

Найбільш типовими задачами, для яких може використовуватися симплексний метод, є оптимальне планування випуску продукції, оптимальний вибір сировини для виробництва продукції, ефективне використання сировинних, матеріальних і енергетичних ресурсів і ін.

2. Алгоритм рішення задачі симплексним методом схематично включає три основних етапи:

1) чітке і ясне математичне формулювання умов задачі і мети її рішення;

2) перебування оптимального рішення шляхом обчислювальних операцій, передбачених алгоритмом симплексного методу;

Дата добавления: 2014-10-31