Методи побудови опорного плану

Для побудови початкового опорного плану транспортної задачі існує кілька методів: північно-західного кута; мінімальної вартості; подвійної переваги; апроксимації Фогеля. Побудову опорного плану зручно подавати у вигляді таблиці, в якій постачальники продукції є рядками, а споживачі — стовпчиками.

Побудову першого плану за методом північно-західного кута починають із заповнення лівої верхньої клітинки таблиці (х ₁₁), в яку записують менше з двох чисел а ₁ та b ₁. Далі переходять до наступної клітинки в рядку або у стовпчику і заповнюють її,і т. д. Закінчують заповнювати таблицю у правій нижній клітинці.

Ідея методу мінімальної вартості полягає в тому, що на кожному кроці заповнюють клітинку таблиці, яка має найменшу вартість перевезення одиниці продукції. Такі дії повторюють доти, доки не буде розподілено всю продукцію між постачальниками та споживачами.

Метод подвійної переваги. Перед початком заповнення таблиці необхідно позначити клітинки, які мають найменшу вартість у рядках і стовпчиках. Таблицю починають заповнювати з клітинок, позначених двічі (як мінімальні і в рядку, і в стовпчику). Далі заповнюють клітинки, позначені один раз (як мінімальні або в рядку, або в стовпчику), а вже потім — за методом мінімальної вартості.

Метод апроксимації Фогеля. За цим методом на кожному кроці визначають різницю між двома найменшими вартостями в кожному рядку і стовпчику транспортної таблиці. Ці різниці записують у спеціально відведених місцях таблиці. Серед усіх різниць вибирають найбільшу і у відповідному рядку чи стовпчику заповнюють клітинку з найменшою вартістю. Якщо ж однакових найбільших різниць кілька, то вибирають будь-який відповідний рядок або стовпчик. Коли залишається незаповненим лише один рядок або стовпчик, то обчислення різниць припиняють, а таблицю продовжують заповнювати за методом мінімальної вартості.

Після побудови першого опорного плану одним із розглянутих методів у таблиці має бути заповнено (m + n – 1) клітинок, де m — кількість постачальників; n — кількість споживачів у задачі, у тому числі фіктивних. Такий план називають невиродженим. Якщо кількість заповнених клітинок перевищує (n + m – 1), то початковий план побудовано неправильно і він є неопорним. Ознакою опорності плану транспортної задачі є його ациклічність, тобто неможливість побудови циклу. Циклом у транспортній задачі називають замкнену ламану лінію, вершини якої розміщуються в заповнених клітинках таблиці, а сторони проходять уздовж рядків і стовпчиків таблиці.

Якщо заповнених клітинок у таблиці менш як (m + n – 1), то опорний план називають виродженим. У такому разі необхідно заповнити відповідну кількість порожніх клітинок, записуючи в них «нульове перевезення», але так, щоб при цьому не порушилася ациклічність плану.

3. Опорний план перевіряють на оптимальність за допомогою потенціалів u_i та v_j відповідно постачальників та споживачів.

Теорема (умова оптимальності опорного плану транспортної задачі). Якщо для деякого опорного плану Х ^* = (x_ij ^*) існують числа u_i та v_j, для яких виконується умова

u_i + v_j = c_ij, x_ij > 0,

u_i + v_j £ c_ij, x_ij = 0

для всіх 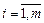та 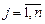, то він є оптимальним планом транспортної задачі.

Потенціали опорного плану визначаються із системи рівнянь u_i + v_j = c_ij, які записують для всіх заповнених клітинок транспортної таблиці.

4. За допомогою розрахованих потенціалів перевіряють умову оптимальності u_i + v_j £ c_ij для порожніх клітинок таблиці. Якщо хоча б для однієї клітинки ця умова не виконується, тобто u_i + v_j > c_ij, то поточний план є неоптимальним і від нього необхідно перейти до нового опорного плану.

Перехід від одного опорного плану до іншого виконують заповненням клітинки, для якої порушено умову оптимальності. Якщо таких клітинок кілька, то для заповнення вибирають таку, що має найбільше порушення, тобто . Для вибраної порожньої клітинки будують цикл перерахування та виконують перерозподіл продукції в межах цього циклу за такими правилами:

1) кожній вершині циклу приписують певний знак, причому вільній клітинці — знак «+», а всім іншим по черзі — знаки «–» та «+»;

2) у порожню клітинку переносять менше з чисел x_ij, що стоять у клітинках зі знаком «–». Одночасно це число додають до відповідних чисел, які розміщуються в клітинках зі знаком «+».

Отже, клітинка, що була вільною, стає заповненою, а відповід­на клітинка з мінімальним числом x_ij вважається порожньою. У результаті такого перерозподілу продукції дістанемо новий опорний план транспортної задачі.

5. Новий опорний план перевіряють на оптимальність згідно з п. 3 розглянутого алгоритму.

Дата добавления: 2014-10-31