
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Метод Гоморі
|
|
|
|
Нехай маємо задачу цілочислового програмування (1)—(4). Для її розв’язування можна скористатися ітеративним методом Гоморі. Суть його полягає ось у чому:
1. Знаходять розв’язок послабленої, тобто задачі без вимог цілочисловості змінних — (1)—(3).
Якщо серед елементів умовно-оптимального плану немає дробових чисел, то цей план є оптимальним планом задачі цілочислового програмування (1)—(4).
2. Коли в умовно-оптимальному плані є дробові значення, то вибирається змінна, яка має найбільшу дробову частину. На базі цієї змінної (елементів відповідного рядка останньої симплексної таблиці, в якому вона міститься) будується додаткове обмеження Гоморі:
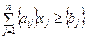 ,
,
де символ {} позначає дробову частину числа.
Для визначення дробової частини будь-якого числа від цього числа віднімають цілу його частину — найбільше ціле число, що не перевищує даного. Цілу частину числа позначають символом []. Наприклад,
[1,3] = 1; [–1,3] = –2;
{1,3} = 1,3 – 1 = 0,3; {–1,3} = –1,3 – (–2) =2 – 1,3 = 0,7.
3. Додаткове обмеження після зведення його до канонічного вигляду і введення базисного елемента приєднується до останньої симплексної таблиці, яка містить умовно-оптимальний план. Здобуту розширену задачу розв’язують, а далі перевіряють її розв’язок на цілочисловість. Якщо він не цілочисловий, то процедуру повторюють, повертаючись до п. 2. Так діють доти, доки не буде знайдено цілочислового розв’язку або доведено, що задача не має допустимих розв’язків у множині цілих чисел.
Досвід показує, що процес розв’язування задач великої розмірності методом Гоморі повільно збіжний. Істотними є також похибки округлення, які можуть призвести до того, що отриманий цілочисловий план не буде оптимальним.
Задача 1. Сільськогосподарське підприємство задумало створити сушильний цех на виробничій площі 190 м2, маючи для цього 100 тис. грн. і можливість придбати устаткування двох типів А і В. Техніко-економічну інформацію про ці два види устаткування подано в таблиці:
| Техніко-економічний показник | Устаткування | Ресурс | |
| А | В | ||
| Вартість, тис. грн. | |||
| Необхідна виробнича площа, м2 | |||
| Потужність, тис. грн./рік | — |
Розв’язування. Нехай х 1 і х 2 — кількість комплектів устаткування відповідно типу А і В.
Запишемо економіко-математичну модель:
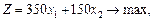
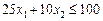 ,
,
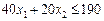 ,
,
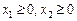 ,
,
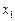 і
і 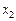 — цілі.
— цілі.
Розв’язуємо задачу, нехтуючи умовою цілочисловості. Остання симплексна таблиця набере вигляду:
| Х баз | С баз | План | ||||
| х 1 | х 2 | Х 3 | х 4 | |||
| х 1 | 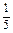
| 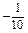
| ||||
| х 2 | 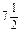
| 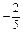
| 
| |||
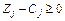
| 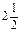
|
Значення другої змінної є дробовим числом, що не задовольняє початкові умови задачі. Побудуємо для другого рядка наведеної симплексної таблиці додаткове обмеження виду 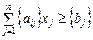 :
:
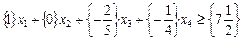 .
.
Оскільки 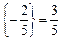 ,
, 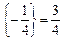 ,
, 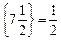 , то додаткове обмеження набирає вигляду
, то додаткове обмеження набирає вигляду
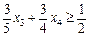 .
.
Зведемо його до канонічної форми та введемо штучну змінну:
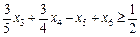 .
.
Приєднавши здобуте обмеження до останньої симплексної таблиці з умовно-оптимальним планом, дістанемо:
| Х баз | С баз | План | – М | |||||
| х 1 | х 2 | х 3 | х 4 | х 5 | х 6 | |||
| х 1 | 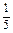
| 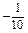
| ||||||
| х 2 | 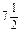
| 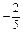
| 
| |||||
| х 6 | – М | 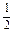
| 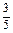
| 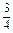
| –1 | |||
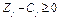
| 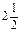
| |||||||
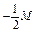
| 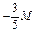
| 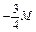
| М |
Розв’язуючи наведену задачу, остаточно знаходимо цілочисловий оптимальний план:  ,
, 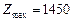 .
.
1.3. Метод «віток і меж»
Ефективнішим за метод Гоморі розв’язування задач цілочислового програмування є метод «віток і меж». Спочатку, як і в разі методу Гоморі, розв’язується послаблена (відкиданням умови цілочисловості) задача.
З цією метою застосовується симплексний метод.
Нехай потрібно знайти хj — цілочислову змінну, значення якої 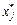 в оптимальному плані послабленої задачі є дробовим. Тоді можна стверджувати, що в інтервалі
в оптимальному плані послабленої задачі є дробовим. Тоді можна стверджувати, що в інтервалі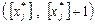 цілих значень немає.
цілих значень немає.
Наприклад, якщо 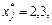 дістаємо інтервал (2,3), де, очевидно, немає хj, яке набуває цілого значення.
дістаємо інтервал (2,3), де, очевидно, немає хj, яке набуває цілого значення.
Значенню 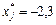 відповідає інтервал (–3; –2), де також не існує цілого значення хj. Отже, допустиме ціле значення xj має задовольняти одну з нерівностей
відповідає інтервал (–3; –2), де також не існує цілого значення хj. Отже, допустиме ціле значення xj має задовольняти одну з нерівностей
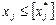 або
або 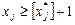 .
.
Приписавши кожну з цих умов до задачі з послабленими обмеженнями, дістанемо дві не пов’язані між собою задачі. Тобто початкову задачу цілочислового програмування (6.1)—(6.4) розіб’ємо на дві задачі з урахуванням умов цілочисловості змінних, значення яких в оптимальному плані послабленої задачі є дробовими. Це означає, що симплекс-методом розв’язуватимемо дві такі задачі:
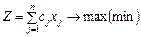 (5)
(5)
за умов
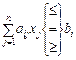 (6)
(6)
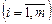 ,
,
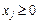
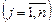 , (7)
, (7)
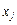 — цілі, (8)
— цілі, (8)
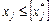 ; (9)
; (9)
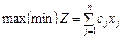 (10)
(10)
за умов
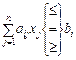 (11)
(11)
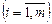 ,
,
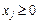
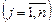 , (12)
, (12)
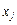 — цілі,
— цілі, 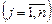 (13)
(13)
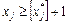 , (14)
, (14)
де 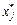 — компонент розв’язку задачі (1)—(4).
— компонент розв’язку задачі (1)—(4).
Далі симплекс-методом розв’язуємо послаблені задачі (6)—(9) і (10)—(14), тобто з відкиданням обмежень (8) і (13). Якщо знайдені оптимальні плани задовольняють умови цілочисловості, то ці плани є розв’язками задачі (1)—(4). Інакше пошук розв’язку задачі триває. Для подальшого розгалуження беремо задачу з найбільшим значенням цільової функції, якщо йдеться про максимізацію, і навпаки — з найменшим значенням цільової функції в разі її мінімізації. Подальше розгалуження виконується доти, доки не буде встановлено неможливість поліпшення розв’язку. Здобутий план — оптимальний.
Розв’язування цілочислових задач методом «віток і меж» можна значно прискорити, приєднавши обмеження виду (9) і (14) до останньої симплекс-таблиці не початкової (1)—(4), а відповідних задач.
Розв’яжемо методом «віток і меж» задачу 1.
Відкинувши умову цілочисловості, дістанемо розв’язок х 1 = 1, х 2 = 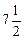 . Отже, допустиме ціле значення х 2 має задовольняти одну з нерівностей
. Отже, допустиме ціле значення х 2 має задовольняти одну з нерівностей 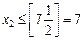 або
або 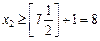 . Далі приєднуємо до задачі кожне з обмежень, нехтуючи умовою цілочисловості, і розв’язуємо по черзі обидві утворені задачі. Для першої (з обмеженням
. Далі приєднуємо до задачі кожне з обмежень, нехтуючи умовою цілочисловості, і розв’язуємо по черзі обидві утворені задачі. Для першої (з обмеженням 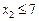 ) оптимальним буде розв’язок
) оптимальним буде розв’язок 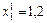 ,
, 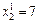 ,
, 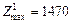 , а для другої (з обмеженням
, а для другої (з обмеженням 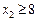 ) — розв’язок
) — розв’язок 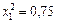 ,
, 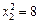 ,
, 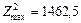 . Оскільки цілочислового плану не знайдено, процес необхідно продовжити, узявши для наступного розгалуження першу задачу, оптимальний план якої дає більше значення функціоналу. Далі розв’язуємо задачу, приєднуючи до неї обмеження
. Оскільки цілочислового плану не знайдено, процес необхідно продовжити, узявши для наступного розгалуження першу задачу, оптимальний план якої дає більше значення функціоналу. Далі розв’язуємо задачу, приєднуючи до неї обмеження 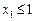 і
і 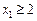 , звідки й знаходимо оптимальний план
, звідки й знаходимо оптимальний план  ,
, 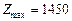 , що збігається з розв’язком, здобутим за методом Гоморі.
, що збігається з розв’язком, здобутим за методом Гоморі.
|
|
|
|
|
Дата добавления: 2014-10-31; Просмотров: 755; Нарушение авторских прав?; Мы поможем в написании вашей работы!