Приклади цілочислових економічних задач. ЛЕКЦІЯ 10-12. Математичні моделі задач дискретного програмування

Метод Гоморі

Постановка задачі

ЦІЛОЧИСЛОВЕ ПРОГРАМУВАННЯ

План

ЛЕКЦІЯ 10-12. Математичні моделі задач дискретного програмування..

1.3. Метод «віток і меж»

У попередніх розділах було розглянуто задачі лінійного програмування та методи їх розв’язування. Ці методи найбільш розроблені, легко реалізуються на ПЕОМ, а тому набули широкого застосування в багатьох галузях науки, техніки та економіки. Проте лінійні моделі відбивають лише певну й вельми обмежену сукупність властивостей навколишнього світу. Адже, скажімо, соціально-економічні процеси не є лінійними. Галузі, об’єднання та окремі підприємства народного господарства функціонують і розвиваються за умов невизначеності, а тому описуються нелінійними, стохастичними, динамічними процесами. Отже, для управління народним господарством, його галузями й тими чи іншими об’єктами господарювання потрібні нелінійні економіко-математичні моделі та методи. А вони ще недостатньо розроблені і до того ж не так легко, як лінійні, піддаються реалізації на ПЕОМ. Щоправда, нелінійні, стохастичні задачі нерідко вдається звести до лінійних, а далі — скористатися відповідними добре розробленими методами розв’язування. Однак такий підхід щоразу потребує певних застережень.

Розглянемо приклад. Урожайність сільськогосподарських культур залежить, як відомо, від багатьох чинників, серед яких насамперед слід назвати заходи з підживлення ґрунту. Природна родючість земельних угідь забезпечує лише певний рівень продуктивності рослин. Щоб підвищити їх урожайність, використовують органічні та мінеральні добрива. Залежність урожайності цукрових буряків від кількості внесених мінеральних добрив ілюструє рис. 6.1.

Із рис. 6.1 бачимо, що за рахунок природної родючості ґрунту та внесення органічних добрив досягається врожайність цукрових буряків 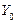. Зі зростанням кількості внесених мінеральних добрив урожайність цієї культури підвищується. Наприклад, якщо ця кількість збільшується від 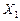до 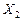(реально це 100—280 кг діючої речовини на гектар), то врожайність цукрових буряків зростає майже лінійно, приблизно від 150 до 450 ц/га. Проте з подальшим збільшенням кількості внесених мінеральних добрив (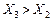) урожайність знижується (), оскільки рослини не за­безпечуються іншими необхідними елементами, наприклад водою.

Отже, якщо в розробленій економіко-математичній моделі вирощування цукрових буряків взяти обмеження за рівнем їх урожайності (скажімо, 150—450 ц/га), то з відповідними застереженнями можна припустити, що існує лінійна залежність між урожайністю цукрового буряку та обсягами внесених органічних добрив.

Зауважимо, що розвиток комп’ютерної техніки і методів математичного моделювання створює передумови для використання нелі­нійних методів, а це може значною мірою підвищити якість розроблюваних планів, надійність та ефективність прийнятих рішень. У цьому розділі стисло розглянемо деякі методи математичного програмування, що вкрай потрібні економістові XXI століття.

Зауважимо, що фахівець, який розробив економіко-математичну модель, але через її складність не реалізував на ПЕОМ, істотно поповнив свої знання про досліджуваний процес, а отже, і прийняті ним (свідомо чи несвідомо) рішення є більш обґрунтованими й економічно ефективними, ніж ті, які могли б постати без вивчення зазначеної моделі.

Дата добавления: 2014-10-31