Метод множників Лагранжа

Для розв’язування задач нелінійного програмування не існує, як уже зазначалося, універсального методу, а тому доводиться застосовувати багато методів і обчислювальних алгоритмів, які ґрунтуються, здебільшого, на теорії диференціального числення, і вибір їх залежить від конкретної постановки задачі та форми економіко-математичної моделі.

Методи нелінійного програмування бувають прямі та непрямі. Прямими методами оптимальні розв’язки відшукують у напрямку найшвидшого збільшення (зменшення) цільової функції. Типовими для цієї групи методів є градієнтні. Непрямі методи полягають у зведенні задачі до такої, знаходження оптимуму якої вдається спрос­тити. До них належать, насамперед, найбільш розроблені методи квадратичного та сепарабельного програмування.

Оптимізаційні задачі, на змінні яких не накладаються обмеження, розв’язують методами класичної математики. Оптимізацію з обмеженнями-рівностями виконують методами зведеного градієнта, скажімо методом Якобі, та множників Лагранжа. У задачах оптимізації з обмеженнями-нерівностями досліджують необхідні та достатні умови існування екстремуму Куна—Таккера.

Розглянемо метод множників Лагранжа на прикладі такої задачі нелінійного програмування:

(1)

за умов

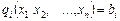(2)

,

де функції і 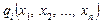диференційовані.

Ідея методу множників Лагранжа полягає в заміні даної задачі простішою: на знаходження екстремуму складнішої функції, але без обмежень. Ця функція називається функцією Лагранжа і подається у вигляді:

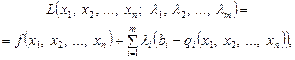(3)

де λ _і — не визначені поки що величини, так звані множники Лагранжа.

Знайшовши частинні похідні функції L за всіма змінними і прирівнявши їх до нуля:

запишемо систему

(4)

що є, як правило, нелінійною.

Розв’язавши цю систему, знайдемо і — стаціонарні точки. Оскільки їх визначено з необхідної умови екстремуму, то в них можливий максимум або мінімум. Іноді стаціонарна точка є точкою перегину (сідлова точка). Отже, для визначення достатніх умов екстремуму та діагностування його типу існує спеціальний алгоритм.

Розв’яжемо методом множників Лагранжа наведену далі задачу.

Задача 1. Акціонерне товариство з обмеженою відповідальністю відвело 1200 га ріллі під основні рослинницькі культури — озиму пшеницю та цукрові буряки.

Техніко-економічні показники вирощування цих культур відбиває таблиця:

Показник	Площа, га, відведена
під озиму пшеницю, х 1	під цукровий буряк, х 2
Урожайність, т/га
Ціна, грн./т
Собівартість, грн./т

Знайти оптимальну площу посіву озимої пшениці та цукрових буряків.

Нехай х ₁ — площа ріллі, відведена під сотні га озимої пшениці; х ₂ — площа ріллі, відведена під цукрові буряки, сотні га.

Зауважимо, що собівартість однієї тони пшениці та цукрових буряків залежить від відповідної площі посіву.

Запишемо економіко-математичну модель. За критерій оптимальності візьмемо максимізацію валового прибутку:

за умов

.

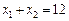Запишемо функцію Лагранжа:

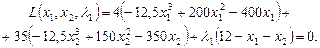
Візьмемо частинні похідні і прирівняємо їх до нуля:

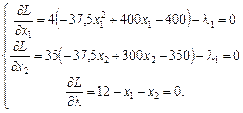
Із цієї системи визначимо сідлову точку. З першої та другої рівностей знайдемо вирази для l₁ і прирівняємо їх:

,

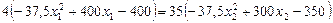або

(6.19)

Із останнього рівняння цієї системи маємо:

.

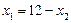Підставивши значення 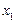у (6.19), дістанемо:

або .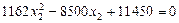

Розв’язавши це квадратне рівняння, дістаємо 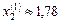(178 га); (553 га).

Відповідно дістаємо: (1022 га); (647 га). Тобто сідловими точками є такі:

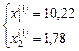
Обчислимо значення цільової функції у цих точках:

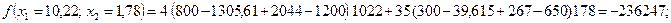
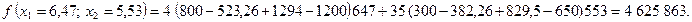Отже, цільова функція набуває максимального значення, якщо озима пшениця вирощується на площі 647 га, а цукровий буряк — на площі 553 га.

Дата добавления: 2014-10-31