Приклади задач нелінійного програмування

Попит на продукцію, що виготовляється на двох видах обладнання, становить 120 одиниць. Собівартість, тис. грн., виробництва одиниці продукції на обладнанні кожної групи залежить від обсягу такого виробництва — відповідно х ₁ і х ₂ — та подається у вигляді для першої групи: ; для другої групи: .

Знайти оптимальний план виробництва продукції на кожній групі обладнання, який за умови задоволення попиту потребує найменших витрат, пов’язаних із собівартістю продукції.

Розв’язування. Математична модель задачі:

за умов

Згідно з методом множників Лагранжа складемо функцію Лагранжа:

.

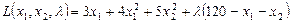Прирівнявши до нуля частинні похідні цієї функції за невідомими параметрами Х ₁, Х ₂ і l, дістанемо систему рівнянь:

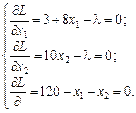
Розв’язавши цю систему, знайдемо:

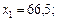
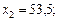
Отже, на першій групі обладнання необхідно випускати 66,5, а на другій 53,5 одиниць продукції. При цьому мінімальні витрати, тис. грн., становитимуть:

Контрольні запитання:

1. В чому особливість задачі нелінійного програмуванн?

2. В чому зміст методу множників Лагранжа?

3. Записати в загальному вигляді формули множників Лагранжа.

Дата добавления: 2014-10-31