
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Розглянемо застосування методу потенціалів для розв’язування транспортних задач, наведених далі
|
|
|
|
Задача 1. Компанія контролює три фабрики А 1, А 2, А 3, здатні виготовляти 150, 60 та 80 тис. од. продукції щотижня. Компанія уклала договір із чотирма замовниками В 1, В 2, В 3, В 4, яким потрібно щотижня відповідно 110, 40, 60 та 80 тис. од. продукції. Вартість виробництва та транспортування 1000 од. продукції замовникам з кожної фабрики наведено в таблиці.
| Фабрика | Вартість виробництва і транспортування 1000 од. продукції за замовниками | |||
| В 1 | В 2 | В 3 | В 4 | |
| А 1 | ||||
| А 2 | ||||
| А 3 |
Визначити для кожної фабрики оптимальний план перевезення продукції до замовників, що мінімізує загальну вартість виробництва і транспортних послуг.
Побудова математичної моделі. Нехай xij — кількість продукції, що перевозиться з і -ї фабрики до j -го замовника 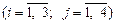 . Оскільки транспортна задача за умовою є збалансованою, закритою
. Оскільки транспортна задача за умовою є збалансованою, закритою 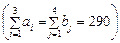 , то математична модель задачі матиме вигляд
, то математична модель задачі матиме вигляд
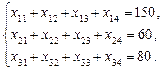
Економічний зміст записаних обмежень полягає ось у чому: уся вироблена на фабриках продукція має вивозитися до замовників повністю.
Аналогічні обмеження можна записати відносно замовників: продукція, що надходить до споживача, має повністю задовольняти його попит. Математично це записується так:

Загальні витрати, пов’язані з виробництвом і транспортуванням продукції, складаються як добуток обсягу перевезеної продукції та питомої вартості перевезень за відповідним маршрутом і за умовою задачі мають бути мінімальними. Тому
Z = 4 × x 11 + 4 × x 12 + 2 × x 13 + 5 × x 14 + 5 × x 21 + 3 × x 22 + x 23 + 2 × x 24 + 2 × x 31 + x 32 +4 × x 33 +2× x 34® min.
У цілому математичну модель поставленої задачі можна записати так:
Z = 4 x 11 + 4 x 12 + 2 x 13 + 5 x 14 + 5 x 21 + 3 x 22 + x 23 + 2 x 24 + 2 x 31 + x 32 +4 x 33 +2 x 34 ® min

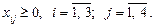
Розв’язування. Розв’язування задачі подамо в таблицях, які назвемо транспортними. Перший опорний план задачі побудуємо методом мінімальної вартості.
| Aj | Bj | ui | |||
| B 1= 110 | B 2= 40 | B 3= 60 | B 4= 80 | ||
    A 1= 150 A 1= 150
| 2 + | 40– | u 1= 5 | ||
 A 2= 60 A 2= 60
| –60 | 0+ | u 2= 2 | ||
| A 3= 80 | u 3= 2 | ||||
| vj | v 1= –1 | v 2= –1 | v 3= –1 | v 4= 0 |
Тому Z = 4 × 110 + 5 × 40 + 1 × 60 + 1 × 40 + 2 × 40 = 820 ум. од.
Перший опорний план транспортної задачі вироджений, оскільки кількість заповнених клітинок у таблиці дорівнює п’яти, а (m + n – 1) = 3 + 4 – 1 = 6. Для подальшого розв’язування задачі необхідно в одну з порожніх клітинок записати «нульове перевезення» так, щоб не порушити опорності плану, тобто можна зайняти будь-яку вільну клітинку, яка не утворює замкненого циклу. Наприклад, заповнимо клітинку А 2 В 4. Тепер перший план транспортної задачі є невиродженим, і його можна перевірити на оптимальність за допомогою методу потенціалів.
На основі першої умови оптимальності ui + vj = cij складемо систему рівнянь для визначення потенціалів плану:
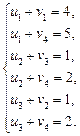
Записана система рівнянь є невизначеною, і один з її розв’язків дістанемо, якщо, наприклад, v 4 = 0. Тоді всі інші потенціали однозначно визначаються: u 1 = 5, u 2 = 2, u 3 = 2, v 1 = –1, v 2 = –1, v 3 = –1.
Далі згідно з алгоритмом методу потенціалів перевіряємо виконання другої умови оптимальності ui + vj ≤ cij (для порожніх клітинок таблиці):
А 1 B 2: u 1 + v 2 = 5 + (–1) = 4 = 4;
А 1 B 3: u 1 + v 3 = 5 + (–1) = 4 > 2;
А 2 B 1: u 2 + v 1 = 2 + (–1) = 1 < 5;
А 2 B 2: u 2 + v 2 = 2 + (–1) = 1 < 3;
А 3 B 1: u 3 + v 1 = 2 + (–1) = 1 < 2;
А 3 B 3: u 3 + v 3 = 2 + (–1) = 1 < 4.
Умова оптимальності не виконується для клітинки А 1 B 3. Порушення D13 = (u 1 + v 3) – c 13 = 4 – 2 = 2 записуємо в лівому нижньому кутку відповідної клітинки.
Перший опорний план транспортної задачі є неоптимальним. Тому від нього необхідно перейти до другого плану, змінивши співвідношення заповнених і порожніх клітинок таблиці.
Потрібно заповнити клітинку А 1 B 3, в якій є єдине порушення умови оптимальності. Ставимо в ній знак «+». Для визначення клітинки, що звільняється, будуємо цикл, починаючи з клітинки А 1 B 3, та позначаємо вершини циклу почергово знаками «–» і «+». Тепер необхідно перемістити продукцію в межах побудованого циклу. Для цього у вільну клітинку А 1 B 3 переносимо менше з чисел хij, які розміщуються в клітинках зі знаком «–». Одночасно це саме число хij додаємо до відповідних чисел, що розміщуються в клітинках зі знаком «+», та віднімаємо від чисел, що розміщуються в клітинках, позначених знаком «–».
У даному випадку  , тобто
, тобто  . Виконавши перерозподіл продукції згідно із записаними правилами, дістанемо такі нові значення: клітинка А 1 B 3 — 40 од. продукції, А 2 B 3 – (60 – 40) = 20 од., А 2 B 4 – (0 + 40) = 40 од. Клітинка А 1 B 4, звільняється і в новій таблиці буде порожньою. Усі інші заповнені клітинки першої таблиці, які не входили до циклу, переписують у другу таблицю без змін. Кількість заповнених клітинок у новій таблиці також має відповідати умові невиродженості, тобто дорівнювати (n + m – 1).
. Виконавши перерозподіл продукції згідно із записаними правилами, дістанемо такі нові значення: клітинка А 1 B 3 — 40 од. продукції, А 2 B 3 – (60 – 40) = 20 од., А 2 B 4 – (0 + 40) = 40 од. Клітинка А 1 B 4, звільняється і в новій таблиці буде порожньою. Усі інші заповнені клітинки першої таблиці, які не входили до циклу, переписують у другу таблицю без змін. Кількість заповнених клітинок у новій таблиці також має відповідати умові невиродженості, тобто дорівнювати (n + m – 1).
Отже, другий опорний план транспортної задачі матиме такий вигляд:
| Aj | Bj | ui | |||
| B 1= 110 | B 2= 40 | B 3= 60 | B 4= 80 | ||
 A 1= 150 A 1= 150
| –110 | 40+ | u 1= 0 | ||
| A 2= 60 | –20 | 40+ | u 2= –1 | ||
| A 3= 80 | 1 + | 40– | u 3= –1 | ||
| vj | v 1= 4 | v 2= –2 | v 3= 2 | v 4= 3 |
Тому Z 2 = 4 × 110 + 2 × 40 + 1 × 20 + 2 × 40 + 1 × 40 + 2 × 40 =740 ум. од.
Новий план знову перевіряємо на оптимальність, тобто повторюємо описані раніше дії. Другий план транспортної задачі також неоптимальний (порушення для клітинки А 3 B 1). За допомогою побудованого циклу виконаємо перехід до третього опорного плану транспортної задачі і дістанемо таку таблицю:
| Aj | Bj | ui | |||
| B 1= 110 | B 2= 40 | B 3= 60 | B 4= 80 | ||
| A 1= 150 | u 1= 2 | ||||
| A 2= 60 | u 2= 0 | ||||
| A 3= 80 | u 3= 0 | ||||
| vj | v 1= 2 | v 2= 1 | v 3= 0 | v 4= 2 |
Тому Z 3 = 4 × 90 + 2 × 60 + 2 × 60 + 2 × 20 + 1 × 40 + 2 × 20 =720 ум. од.
Перевірка останнього плану на оптимальність за допомогою методу потенціалів показує, що він оптимальний. Тому
 ;
;
За оптимальним планом перевезень перший замовник отримує 90 тис. од. продукції з першої фабрики та 20 тис. од. — з третьої. Другий споживач задовольняє свій попит за рахунок виробництва та перевезення 40 тис. од. продукції з третьої фабрики і т. д. При цьому загальна вартість виробництва та перевезення всієї продукції є найменшою і становить 720 ум. од.
Задача 2. Районне агропромислове об’єднання складається з трьох господарств А 1, А 2, А 3, що спеціалізуються на вирощуванні ранніх овочів. Кожне господарство щотижня збирає відповідно 50, 30 та 20 т овочів, які необхідно відправляти в чотири магазини B 1, B 2, B 3, B 4. Магазини бажають отримувати ранні овочі в кількості відповідно 30, 30, 10 та 20 т. Вартість перевезення 1 т овочів від господарства до магазинів наведено в таблиці.
| Господарство | Вартість перевезення 1 т овочів у магазини | |||
| В 1 | В 2 | В 3 | В 4 | |
| А 1 | ||||
| А 2 | ||||
| А 3 |
Визначити такий план перевезення овочів до магазинів, за якого загальні витрати агропромислового об’єднання будуть найменшими.
Побудова математичної моделі. Нехай хij — кількість тон овочів, які перевозять з і -го господарства j -го магазину ( ;
;  ). Тоді економіко-математична модель поставленої задачі має такий вигляд:
). Тоді економіко-математична модель поставленої задачі має такий вигляд:
Z = 2 x 11 + 3 x 12 + 4 x 13 + 2 x 14 + 5 x 21 + 7 x 22 + x 23 + 4 x 24 + 9 x 31 + 4 x 32 +3 x 33 +2 x 34 ® min,
за обмежень


Знак «≤» у перших трьох обмеженнях задачі пояснюється тим, що за умовою транспортна задача є відкритою:
У такій ситуації, коли попит менший за пропозицію, частина овочів залишиться в господарствах і фактично буде вивезено менше, ніж зібрано.
Розв’язування. Щоб визначити оптимальний план поставленої задачі, її необхідно збалансувати, тобто звести до закритого типу. Це виконується шляхом уведення додаткового, умовного споживача B 5 із попитом B 5 = 100 – 90 = 10 т. Вартість перевезення одиниці продукції до умовного споживача дорівнює нулю.
Перший опорний план транспортної задачі побудуємо методом подвійної переваги.
| Aj | Bj | ui | ||||
| B 1 = 30 | B 2= 30 | B 3= 10 | B 4= 20 | B 5= 10 | ||
| A 1= 50 | u 1= –4 | |||||
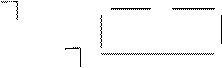 A 2= 30 A 2= 30
| –10 | 0+ | u 2= 0 | |||
| A 3= 20 | 1 + | 20– | u 3= –2 | |||
| vj | v 1= 6 | v 2= 7 | v 3= 1 | v 4= 0 | v 5= 0 |
Перший опорний план є виродженим, і тому в клітинку, наприклад A 2 B 4, поставимо нуль і вважатимемо її заповненою.
Перевірка плану за допомогою потенціалів показує, що він є неоптимальним. Перехід до другого опорного плану виконується шляхом заповнення клітинки A 3 B 2 згідно із побудованим циклом. Зазначену клітинку включено до циклу тому, що в разі кількох однакових найбільших порушень (D21 = D32 = 1) заповнюють таку клітинку таблиці, яка має меншу вартість перевезення одиниці продукції (с 32 < c 21).
Другий план транспортної задачі наведемо у вигляді таблиці:
| Aj | Bj | ui | ||||
| B 1= 30 | B 2= 30 | B 3= 10 | B 4= 20 | B 5= 10 | ||
| A 1= 50 | u 1= –3 | |||||
| A 2= 30 | u 2= 0 | |||||
| A 3= 20 | u 3= –2 | |||||
| vj | v 1= 5 | v 2= 6 | v 3= 1 | v 4= 4 | v 5= 0 |
Умова оптимальності для цього опорного плану виконується, і тому можна записати:
 ;
;
Z min = 2 × 30 + 3 × 20 + 1 × 10 + 4 × 10 + 4 × 10 + 2 × 10 = 320 ум. од.
Згідно з оптимальним планом потреба магазинів у ранніх овочах задовольняється завдяки повному вивезенню продукції з першого та третього господарств і лише частково — з другого (залишок дорівнює 10 т). У цьому разі загальна вартість усіх перевезень буде найменшою і становитиме 230 ум. од.
Але виявляється, що розглянута транспортна задача має ще один альтернативний оптимальний план. Ознакою цього є виконання умови оптимальності для порожньої клітинки: ui + vj = cij. В останній таблиці це справджується для порожньої клітинки A 2 B 1: u 1 + v 1 = 0 + 5 = с 21 = 5.
Щоб отримати альтернативний оптимальний план, достатньо заповнити зазначену клітинку таблиці, виконавши перерозподіл продукції за таким циклом:
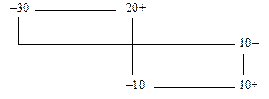
Наведемо транспортну таблицю, що відповідає другому оптимальному плану задачі.
| Aj | Bj | ui | ||||
| B 1 = 30 | B 2 = 30 | B 3 = 10 | B 4 = 20 | B 5 = 10 | ||
| А 1 = 50 | u 1 = –3 | |||||
| A 2 = 30 | u 2 = 0 | |||||
| A 3 = 20 | u 3 = –2 | |||||
| vj | v 1 = 5 | v 2 = 6 | v 3 = 1 | v 4 = 4 | v 5 = 0 |
Тому
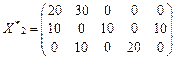 ;
;
Z min = 2 × 20 + 3 × 30 + 5 × 10 + 1 × 10 + 2 × 20 = 230 ум. од.
Другий оптимальний план задачі формулюється так. Перевезти з першого господарства 20 т овочів до першого магазину та 30 т — до другого; з другого господарства — 10 т до першого магазину та 10 т овочів до третього, залишаючи невивезеними 10 т, а також з третього господарства до четвертого магазину — 20 т овочів. У цьому разі загальні транспортні витрати становитимуть 230 ум. од. і також будуть найменшими.
Задача 3. Три нафтопереробних заводи А 1, А 2, А 3, із максимальною щоденною продуктивністю відповідно 30, 20, 15 тис. т бензину забезпечують чотири бензосховища B 1, B 2, B 3, B 4, потреба яких становить відповідно 10, 20, 25 та 20 тис. т. бензину. Бензин транспортується до бензосховищ за допомогою трубопроводів. Вартість перекачування 1000 т бензину від заводів до сховищ (в умовних одиницях) наведено в таблиці.
| Завод | Вартість, ум. од., перекачування 1000 т бензину до сховищ | |||
| В 1 | В 2 | В 3 | В 4 | |
| А 1 | ||||
| А 2 | ||||
| А 3 |
Cформулювати та розв’язати відповідну транспорту задачу з неодмінним виконанням таких умов:
1) повністю задовольнити попит бензосховища B 4;
2) недопостачання бензину до сховища B 2 штрафується 5 ум. од. вартості за кожні 1000 т бензину;
3) у зв’язку з виконанням ремонтних робіт на трубопроводі постачання бензину із заводу А 1 до сховища B 1 тимчасово неможливе.
Розв’язування. Визначимо, до якого типу належить транспортна задача:
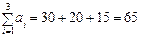 ,
,  .
.
За умовою транспортна задача є відкритою, незбалансованою. Зведення її до закритого типу потребує введення додаткового фіктивного постачальника А 4 з продуктивністю а 4 = 75 – 65 = 10 (тисяч тон). Кількість бензину, що «відправляється» фіктивним заводом до бензосховищ, в оптимальному плані означатиме обсяг незадоволеного попиту в цьому пункті призначення. Тому для виконання першої додаткової вимоги задачі необхідно блокувати клітинку фіктивного постачальника А 4 та споживача B 4, записавши в ній досить високу вартість М. Тоді в оптимальному плані транспортної задачі ця клітинка обов’язково буде незаповненою.
Виконання другої умови задачі забезпечується тим, що в рядку фіктивного постачальника у стовпчику B 2 вартість транспортування 1000 т бензину дорівнюватиме 5 ум. од. замість нуля.
Оскільки неможливо транспортувати бензин від заводу А 1 до сховища B 1, необхідно також блокувати маршрут А 1 B 1. Для цього в зазначеній клітинці замість с 11 = 4 записуємо величину М.
З огляду на викладене таблиця для першого плану транспортної задачі має такий вигляд (початковий опорний план побудовано методом апроксимації Фогеля).
| Aj | Bj | ui | Різниці для рядків | |||
| B 1= 10 | B 2= 20 | B 3= 25 | B 4= 20 | |||
 A 1= 30 A 1= 30
| М | –15 | 10+ | u 1= 0 | 2 2 2 | |
| A 2= 20 | u 2= –1 | 3 3 3 | ||||
| A 3= 15 | –10 | 5+ | u 3= –2 | 2 5 | ||
| A 4= 10 | М – 4 | М – 7 | М – 4 | М 10– | u 4= М –7 | |
| vj | v 1= 3 | v 2= 5 | v 3= 3 | v 4= 7 | ||
| Різниці для стовпчиків | 2 2 1 | 1 1 1 | 2 2 2 |
Отже, перший опорний план задачі неоптимальний. Найбільше порушення умови оптимальності відповідає порожнім клітинкам А 4 B 1 та А 3 B 3 таблиці. Оскільки обидві вони мають однаковий коефіцієнт с 41 = с 43 = 0, то для заповнення можна вибрати будь-яку з них, наприклад А 4 B 1. Перехід до другого плану виконується за таким циклом:
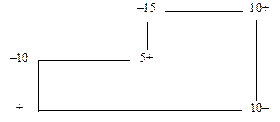
При цьому заблокована клітинка А 4 B 4 звільняється.
Подальше розв’язування задачі подано у вигляді таблиць.
| Aj | Bj | ui | |||
| B 1= 10 | B 2= 20 | B 3= 25 | B 4= 20 | ||
   A 1= 30 A 1= 30
| М | +5 | 20– | u 1= 0 | |
  A 2= 20 A 2= 20
| –20 | + 5 | u 2= –1 | ||
| A 3= 15 | u 3= –2 | ||||
| A 4= 10 | М | u 4= –3 | |||
| vj | v 1= 3 | v 2= 5 | v 3= 3 | v 4= 7 |
| Aj | Bj | ui | |||
| B 1= 10 | B 2= 20 | B 3= 25 | B 4= 20 | ||
| A 1= 30 | М | М | u 1= 0 | ||
| A 2= 20 | u 2= –1 | ||||
| A 3= 15 | u 3= –2 | ||||
| A 4= 10 | М | u 4= –3 | |||
| vj | v 1= 3 | v 2= 5 | v 3= 3 | v 4= 6 |
В останній таблиці маємо оптимальний план транспортної задачі.
Тому
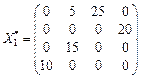 ,
,
Z min = 5 × 5 + 5 × 25 + 5 × 20 + 3 × 15 = 245 ум. од.
Через незбалансованість поставленої транспортної задачі спостерігатиметься недопостачання бензину до першого бензосховища в кількості 10000 т. Загальні витрати на транспортування в цьому разі будуть найменшими і становитимуть 245 ум. од.
Альтернативний оптимальний план дістанемо, заповнивши клітинку А 4 В 3 (для неї u 4 + v 3 = c 43) згідно з таким циклом:
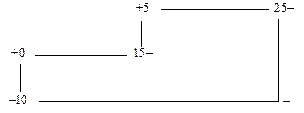
Тоді можна записати:
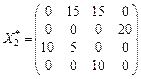 ,
,
Z min = 5 × 15 + 3 × 15 + 5 × 20 + 1 × 10 + 3 × 15 = 245 ум. од.
Мінімальні загальні витрати на транспортування в розмірі 245 ум. од. відповідають також ще одному оптимальному плану задачі, згідно з яким третє бензосховище отримає на 10000 т бензину менше, ніж потребує.
Існування двох альтернативних оптимальних планів розглянутої транспортної задачі розширює можливості стосовно остаточного прийняття рішення.
|
|
|
|
|
Дата добавления: 2014-10-31; Просмотров: 915; Нарушение авторских прав?; Мы поможем в написании вашей работы!