Электрбайланыс сигналдары

ДИКМ

Кодирование с предсказанием

Для реального сигнала (телефонного, телевизионного) более вероятны низкочастотные составляющие спектра. Кроме того, частоту дискретизации на практике выбирают выше, чем по Котельникову. Это означает, что значения соседних отсчетов непрерывного сигнала с большой вероятностью мало отличаются друг от друга. Передача кодированных значений отсчетов непрерывного сигнала (ИКМ) является неэффективной, т.к. канал будет загружен наряду с полезной также и избыточной (известной на приеме) информацией. Устранение этой избыточности создает условия для передачи большего количества информации.

Повысить эффективность систем передачи информации позволяет передача кодированных значений отсчетов сигнала ошибки предсказания (кодирование с предсказанием). Сигнал ошибки предсказания представляет собой разность между истинным и предсказанным сигналами. Предсказанный сигнал формируется из предыдущих отсчетов сигнала.

Дифференциальная импульсно-кодовая модуляция (ДИКМ) - импульсно-кодовое представление значений отсчетов сигнала ошибки предсказания. Другими словами отсчеты сигнала ошибки предсказания подвергают обычным операциям квантования и кодирования.

Известно большое число вариантов технической реализации кодирования с предсказанием, которые отличаются операцией формирования сигнала ошибки предсказания. Наиболее широкое распространение получила схема модулятора с обратной связью. В этой схеме кодируются значения разности между данным отсчетом и квантованным предыдущим отсчетом.

Рисунок 24.2 – Принцип формирования ДИКМ сигнала.

Шум квантования при ДИКМ меньше, чем при ИКМ при том же числе уровней квантования. Качество передачи при ДИКМ такое же, как и при ИКМ при меньшем числе символов в кодовой комбинации (на один-два и белее символов). Шум ложных импульсов при ДИКМ в большей мере, чем при ИКМ, ухудшает верность приема.

24.3 Дельта-модуляция

Дельта-модуляция (ДМ) – представление значений отсчетов сигнала ошибки предсказания с помощью двухуровнего (+1 или -1) одноразрядного кода при большой частоте дискретизации. Сигнал на выходе дельта-модулятора содержит лишь сведения о полярности (знаке) сигнала ошибки предсказания.

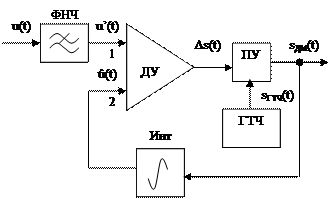
Рисунок 24.3 – Структурная схема модулятора ДМ.

ФНЧ ограничивает спектр частот входного сигнала 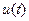. ДУ усиливает разность двух сигналов 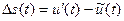. Генератор тактовой частоты (ГТЧ) вырабатывает тактовые импульсы 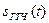, которые поступают на пороговое устройство (ПУ). ПУ формирует ДМ сигнал 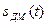: на его выходе возникают импульсы положительной полярности, если на выходе ДУ в момент прихода тактового импульса разностный сигнал положительный 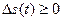, и импульсы отрицательной полярности, если он отрицательный 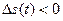. В цепь обратной связи включается Инт, на выходе которого формируется аппроксимирующий ступенчатый сигнал . При ДМ соседние значения ступенчатого напряжения различаются обязательно на один шаг квантования.

2.1.Электрбайланыс сигналдарының жіктелуі.

Формасына қарай жай және күрделі сигналдар болып бөлінеді.

Жай сигналдар жай математикалық формула ретінде келтіруге болатын уақыт функциясы болып табылады.

Жай сигналдардың мысалдары: гармоникалық; бірлік функциямен анықталатын, тұрақты; дельта-функциямен анықталатын.

Синус және косинус функцияларымен анықталатын сигналдар гармоникалық функция деп аталады:

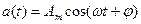или .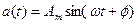

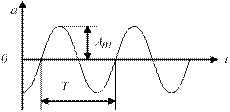
2.1-сурет – Гармоникалық тербеліс.

Параметрлері: амплитуда 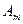;жиілік: ,

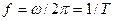мұндағы ω –бұрыштық жиілік.: [ ω ]=рад/с; - циклдік жиілік.

Шама бірлігі: [ f ]=Гц; Т – период.Шама бірлігі: [ T ]=с; 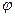, 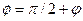-бастапқы фаза.

Уақыттың кез келген мезетінде өзгеріссіз болып қалатын функциялар тұрақты деп аталады: .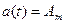

2.2-сурет –Тұрақты сигнал.

Бірлік функция ток пен кернеудің сатылы төмендеуінің математикалық анықтамасы болып табылады:

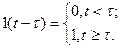
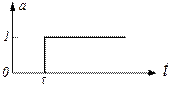
2.3-сурет –Бірлік функция.

Дельта-функция аз ұзақтық пен үлкен амплитуданың тік бұрышты математикалық анықтамасы болып табылады:

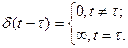
2.4- Сурет – Дельта-функция.

Күрделі сигналдар уақыттың жай математикалық анықтамамен сипаттауға болмайтын функциясы болып табылады.Күрделі сигнал Фурье қатарына түрленуі мүмкін:

,

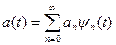Мұндағы 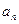--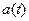дан тәуелді ыдырау коэффициенты;

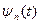- базистік функциялар –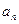коэффициенттерін жеңіл табуға мүмкіндік беретін жай аналитикалық мәндерді анықтайтын функциялар.

Күрделі сигналдардың мысалдары: хабарларды көрсететін импульстік сигналдар.

Шектелген уақыт аралығында нөлден өзге сигналдар импульстік деп аталады. Жалғыз тікбұрышты сигналдар және тікбұрышты импульстардың периодтық тізбектігі көп сұранысқа ие.

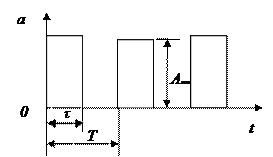
2.5-сурет – ПППИ.

Параметрлер: А_m – амплитуда; τ –импульс ұзақтығы Т – период;

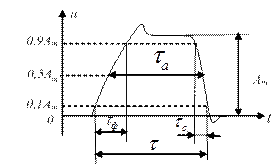
2.6 - сурет – тікбұрышты форманың реальді формасы.

Параметрлері: А_m – амплитуда; τ – импульс ұзақтығы; τ_а – импульстің активті ұзақтығы; τ_ф –фронт ұзақтығы; τ_c –түсу ұзақтығы.

Информативтігі бойынша кездейсоқ және детерленген сигналдар болып ажыратылады.

Детерленген сигналдарға уақыттың кез келген мезетінде мәндері ашық болатын сигналды айтамыз. Олардың математикалық сипаттамасы ретінде детерленген математикалық модельдер жатады. Мұндай сигналдар хабар таратқыш болып саналмайды.

Детерленген сигналдардың мысалдары:белгілі параметрлері бар гармоникалық сигналда;параметрлері және формалары белгілі импульстер.

Детерленген сигналдардың келесі түрлерін ажыратылады:

- периодтық – уақыттың белгілі тең аралығында қайталанып тұратын период деп аталатын сигналдар;

- периодтық емес – бір рет қана болып, қайталанбайтын сигналдар.

Кездейсоқ сигналдар деп уақыттың кез келген мезетінде белгісіз болатын сигналдарды айтамыз. Олардың математикалық сипаттамасы ретінде математикалық формасы болып табылады. Тек кездейсоқ сигналдар хабарды тасымалдағыш болып табылады. Тек реалды сигналдар әрқашан кездейсоқ болып табылады.

Кездейсоқ сигналдардың мысалдары: телеграфтық, телефондық, радиохабарлағыш, факсимильді, телевизиялық, мәліметтер тасымалдағыш.

Сипаттамасы бойынша сигналдың 4 түрі бар:

- деңгейі және уақыт бойынша үздіксіз. Бей интервалда кез келген мәнді қабылдайды және кез келген уаұыт мезетінде өзгеріп отырады;

t

2.7 – сурет –үздіксіз сигнал.

- деңгейі бойынша үздіксіз, уақыт бойынша дискретті. Кей интервалда кез келген мәндер қабылдайды, бірақ уақыттың белгілі, алдын ала анықталған мезеттерінде өзгеріп отырады.

2.8 - сурет –уақыт бойынша дискретті сигнал.

- деңгейі бойынша дискретті, уақыт бойынша үздіксіз. Уақыттың белгілі аралығында тек рұқсат етілген мәндерді қабылдайды;

2.9 - сурет –деңгей бойынша дискретті сигнал.

- деңгей және уақыт бойынша дискретті сигналдар. Уақыттың дискретті кезеңдерінде дискретті мәндерді қабылдайды.

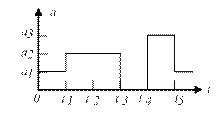
2.10 - сурет – Дискретті сигнал.

Цифрлы сигналдар – дискретті сигналдардың беріліп отырған дискретті сигналдың рұқсат етілген деңгейлері сан түрінде келтірілген түрі. Байланыс жүйелерінде екілік, үштік, төрттік және т.б. цифрлы сигналдар қолданылады.

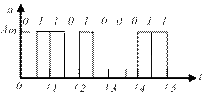
2.11 – сурет – екілік цифрлы сигнал.

2,2. Электрбайланыс сигналдарының сипаттамалары.

Пайдалы сигнал тасымалдау объектісі болып табылады, ал байланыс техникасы – сигналдардың байланыс арналары бойынша тасымалдау техникасы. Тасымалдауы бойынша сигналдың негізгі параметрлері:

Сигнал ұзақтығы 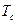-сигнал жасайтын уақыт интервалы;

Сигнал спектрінің ендігі 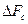- сигналдың энергиясының бөлігі орналасқан жиілік диапазоны;

Динамикалық диапазон 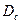-сигнал деңгейлерінің өзгеріс диапазоны. Децибелде өлшенеді (дБ):

,

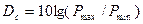Мұндағы 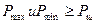-лездік қуаттың максимал және минимал мәндері;

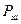- арнадағы шуылдың орташа қуаты.

Динамикалық диапазон қуатпен қоса ток және кернеу бойынша анықталады:

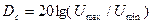немесе ,

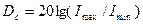Мұндағы 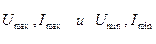-лездік ток немесе кернеудің максимал және минимал мәндері.

Жалпылыма сипаттамасы болып сигнал мөлшері табылады:

.

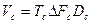Сигналдың мөлшері тасымалданатын хабардың мөлшеріне пропорционалды. Сигнал мөлшері неғұрлым үлкен болған сайын осы мөлшерге соғұрлым көп хабар енгізуге болады және мұндай сигналды байланыс арнасы бойынша қажетті сапамен жеткізу қиын болады.

Сигналдың өзге сипаттамалары:

- сигнал базасы: . Егер В_с≤1, сигналды таржолақты деп атаймыз, ал егер В_с>>1 – кеңжолақты болып табылады;

-сигнал амплитудасының коэффициенті: ,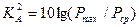

мұндағы 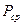- сигналдың орташа қуаты.

3 Сигналдардың көрсетілу тәсілдері

3.1 сигналдың математикалық үлгісі

Оның математикалық анықтамасы, сигналдың қасиеттері мен сипаттамаларын анықтауға болатын сәйкесінше оңай математикалық мәннің алыну тәсілі.

Мысал: .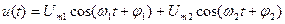

Математикалық үлгіні таңдау уақыт диаграммасы негізінде жасалады. Бір сигнал бірнеше үлгілерде келтірілуі мүмкін.

Кемшілігі:күрделі сигнал формасы бойынша таңдау қиындығы.

3.2 Сигналдың уақыттық диаграммасы.

Уақытқа тәуелді жасалатын сигналдың лездік мәндерінің қисығы. Сигналдың берілу формасы сигналдың энергиясы, қуаты, ұзақтығы секілді сипаттамаларын анықтауға мүмкіндік береді. Интервалдағы [ t₁, t₂ ] сигнал қуаты:

.

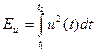Кедергісі 1 Ом болатын резистордағы энергия дәл осындай болады, егер қысқыштарына u(t) кернеуі берілсе. Периодты сигналдың энергиясы шексіз үлкен.Сондықтан сигналдың қуаты туралы айту қажет, демек уақыт бірлігіндегі энергия туралы.

Мысал:

3.1- сурет –уақыттық диаграмма.

Уақыттық диаграмманы осциллограф көмегімен анықтауға болады.

Артықшылығы:айқындығы.

Кемшілігі: ұзақ сигналдардың берілуінде және теориялық есептеулерде қолдануға ыңғайсыз болып келеді.

3.3 Сигналдың спектрлік диаграммасы

Оның спектрінің графикалық кескіні.

Егер қандай да бір сигнал гармоникалық тербелістердің соммасы ретінде берілер болса, осы сигналдың спектрлік ыдырауы іске асқан болып табылады. Бөлек гармоникалық сигнал компоненттерінің жиынтығы оның спектрін құрайды.

Олар амплитудалық және фазалық болып бөлінеді.

Сигналдың амплитудалық спектрлік диаграммасы – сигналдың гармоникалық құраушыларының амплитудаларының жиілік бойынша таралуы. Онда сигналдың орналасу энергиясының түрлі жиіліктік құраушылар туралы маңызды хабар беріледі. Мысал:

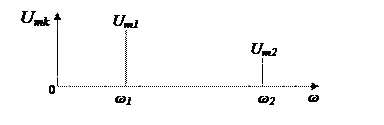
3.2 – сурет –Амплитудалық спектрлік диаграммасы.

Сигналдың фазалық спектрлік диаграммасы – сигналдың гармоникалық құраушыларын фаза жиіліктері бойынша орналастыру диаграммасы. Гармоника фазалары[ -π, π ] интервалында оң және теріс мәндер қабылдауы мүмкін. Мысал:

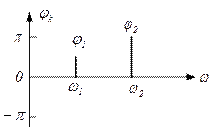
3.3-сурет –фазалық спектрлік диаграмма.

Спектрлік диаграммаларды спектр анализаторы арқылы бақылауға болады.

Артықшылықтары: спектрді білу сигналдың байланыс арнасы бойынша өзгеріссіз тасымалдануын, сигналдың айырылуы және кедергілердің әлсіреуін іске асырады.

Кемшіліктері: сигнал формасы спектрдің амплитудалық және амплитудалық құраушылары арқылы анықталады.

3.4 Сигналдың векторлық диаграммасы

Бұл токтар мен кернеулердің координаттық жазықтықта гармоникалық тербелістермен айқындалған векторлар арқылы берілуі. Координаттық жазықтықта әр түрлі жиіліктегі гармоникалық тербелістерді бейнелейтін векторлар координата басында әр түрлі жылдамдықпен сағат тіліне қарсы айналады. Олардың модулі тербеліс амплитудасымен, ал санақ басталғандағы бұрылу бұрышы – бастапқы фазалардың мәндерімен анықталады. Векторлардың абсцисса осіне проекциялары косинусоидалды тербелістер, ал ордината осіне- синусоидалды болып табылады. Олар ток пен кернеулердің лездік мәндері уақыт бойынша өзгертулерін көрсетеді.

Мысал:

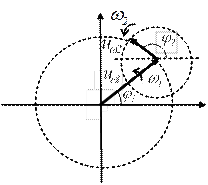
Артықшылығы: спектрлік ыдыраудың интерпретация айқындығы.

Кемшілігі: токтың немесе кернеудің уақыт бойынша көрсетілу ыңғайсыздығы.

4 Сигнал спектрі.

4.1 спектр түрлері.

Спектр түрі сигнал сипатына қарай анықталады.

Дискретті (жолақты) және үздіксіз(тұтас) спектрлер болып бөлінеді.

Егер сигналды гармоникалық тербелістердің қорытынды соммасы немесе тізбегі ретінде қарастыруға болса, спектр дискретті болады. Ол спектралды диаграммада бөлек спектралды сызықтардың жиынтығы ретінде келтіріледі.

Периодты және квазипериодты сигналдар дискретті спектрге ие.

Мәндері период деп аталатын белгілі, өзара тең уақыт бөліктерінде қайталанатын сигналдар периодтық деп аталады. Периодты сигналдардың спектр ерекшелігі гармоника жиіліктері 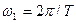негізгі жиілікке еселеуіш болып келеді. Мұндай спектрлерді гармоникалық деп атаймыз.

Периодты емес сигналдардың бір түрі болып квазипериодикалық сигналдар табылады. Жартылай период болып табылатын белгілі бір уақыт аралығында жақын мәнде қайталанып тұратын мәндер.

Мысал: .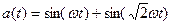

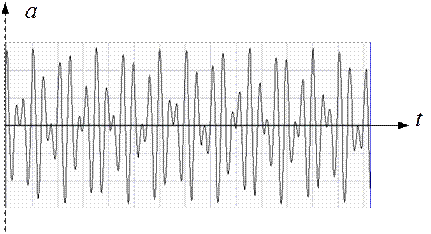
4.1 - сурет – Квазипериодикалық сигнал.

Квазипериодикалық сигналдардың ерекшелігі гармоника жиіліктері еселі қатынаста болмайтындығы болып табылады. Мұндай спектрлер гармоникалық болып саналмайды.

ω

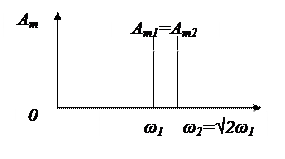
4.2 - сурет – Дискретті спектр.

Егер сигналды жиіліктері бір біріне шексіз жақын орналасқан амплитудасы бойынша шексіз аз болып келетін шексіз үлкен санның соммасы ретінде қарастыра алсақ, спектр үздіксіз болып саналады. Амплитудалық спектральді диаграммалардың ординаталар осі бойынша амплитудалардың спектральді тығыздығы, ал фазалықта – фазалардың спектральды тығыздығы орналасады.

Периодикалық емес және хаотикалық тербелістердің үздіксіз спектрі болады.

Амплитудалардың спектральді тығыздығы 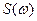- элементар гармоникалар амплитудасы туралы хабар тасымалдайтын жиілік функциясы. Ол жиілік осі бойынша сигнал гармоникаларының амплитудаларының тұтастай орналасу интенсивтілігін сипаттайды.

.

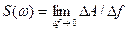Шама бірлігі В/Гц немесе А/Гц.

ω

4.3 - сурет –ОПИ амплитудалық спектралды диаграммасы.

Фазалардың спектральды тығыздығы 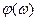–элементар гармоникалар туралы хабар таситын жиілік функциясы.

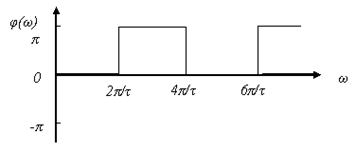
4.4- сурет –ОПИ фазалық спектралды диаграммасы.

Шекті және шексіз спектрге ажыратамыз.

Шекті спектр деп периодикалық немее квазипериодикалық сигналдың барлық спектралды сызықтар орналасқан және периодикалық емес сигналдың спектрал тығыздығы нөлден өзге мән қабылдайтын кездегі жиіліктер интервалын айтамыз. Егер бұл интервал шексіз болса, спектр шексіз болып табылады.

4.5 – сурет –шектелген спектр.

4.2 Электрбайланыстың алғашқы сигналдары.

Дата добавления: 2014-10-31