Котельников теоремасы 1 страница

Котельников теоремасы (дискретизация теоремасы):

F_max жиілігімен шектелген кез келген үздіксіз сигнал Δt≤1/(2F_max) уақыт интервалы арқылы алынған лездік мәндердің тізбектелуі ретінде бейнеленуі мүмкін.

Теорема бойынша шектеулі спектрі бар үздіксіз сигналды Котельников қатарына орналастыруға болады.:

,

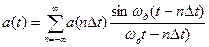мұндағы 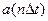- уақыттың дикретті мезетіндегі сигналды есептеу;

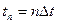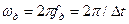-дискретизация жиілігі;

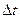- дискретизация интервалы;

-есептеу функциясы.

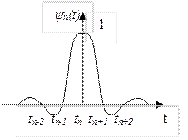
7.1-сурет –есептеу функциясы.

Кез келген реалды сигнал соңғы ұзақтыққа ие. Оны Котельников қатарының қысқа түрімен келтіруге болады:

,

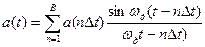мұндағы B=T_c/Δt+1=2F_maxT_c+1≈2ΔF_cT_c – ұзақтығы Т_с болатын сигналды есептеу саны.

7.2 Котельников теоремаының мазмұны

1. Теорема a(t) сигналының түрін айқындамайды, демек ол кездейсоқ болуы да мүмкін.

2. Теорема бойынша a(t) сигналындағы барлық мәлімет a(nΔt) таңдау бойынша алынған мәндерінде жатады. Демек, байланыс арнасы бойынша үздіксіз сигнал уақыт бойынша дискретті a_д(t) сигналына түрленуі мүмкін. Үздіксіз сигналдың санау тізбегі бойынша берілуі дискретизация деп аталады. Практикада әрбір санау a(nΔt) және τ<<Δt ұзақтығымен есептелінеді.

7.2 -сурет–үздіксіз сигналдың дискретизациясы.

3. Теорема a(t) үздіксіз сигналының қабылдағыштағы санаулары бойынша қалпына келуін анықтайды, әр санауды ψ_n(t) санау функциясына көбейту және шыққан мәндерді қосу керек

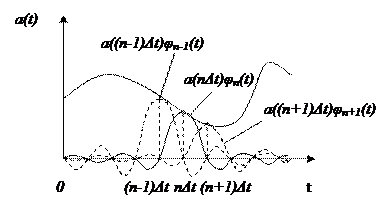
7.3-сурет –үздіксіз сигналдың қалпына келуі.

7.3 Котельников теоремасын қолдану

Теорема арналары уақыт бойынша бөлінген (УББ) тасымалдау жүйелерін(ТЖ) құрудың теориялық негізі болып саналады.

a₁(t)

УББ-ның міндеті арналар кезек бойынша бір жиілік жолағын пайдалануында.

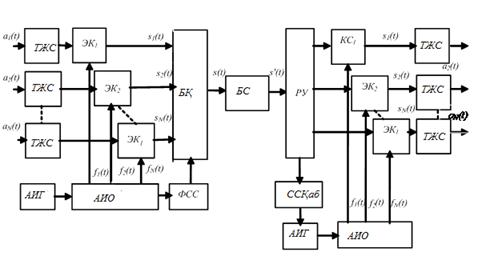
7.4-сурет – ТЖ мен УББ-ның құрылымдық сұлбасы

Сұлбадағы белгіленулер:

a₁(t), a₂(t), …, a_n(t) – біріншілік сигналдар;

ТЖС – төменгі жиіліктер сүзгісі. F_max жиілігі бар біріншілік сигналдардың тасымалданудағы жиіліктер жолағын шектейді және қабылдағыштарындағы санау тізбектерінен біріншілік сигналдарды қалпына келтіреді;

ЭК₁, ЭК₂, …, ЭК_N –арналық электронды кілттер. Жиілігі бойынша шектеулі біріншілік сигналдарда дискретизация операциясын атқарады;

f₁(t), f₂(t),..., f_N(t) – ПППИ Δt периоды және ұзақтығы τ<<Δt;

АИГ –арналық импульстер генераторы;

АИО –арналық импульстерді орналастырғыш;

s₁(t), s₂(t), …, s_N(t) –арналық сигналдар;

БҚ –біріктіргіш құрылғы. Арналық сигналдарды біріктіреді.

СС – синхросигнал. Тасымалдануда арналық ЭК-нің және қабылдағыштағы КС-нің синхронды жұмысын қамтамасыз етеді. Арналық сигналдардың импульсінен міндетті түрде ерекшеленеді (амплитудамен, ұзақтықпен және т.б.);

ФСС – СС орнатқыш;

s(t) –ЛС кірісіндегі топтық сигнал;

БС – байланыс сызығы;

s’(t) –ЛС шығысындағы кедергілер мен бұрмаланулар есебінен өзгеріске ұшыраған топтық сигнал;

ШҚ –шешкіш құрылғы. Кірісінде арналық сигналдар мен СС-ның айырылуын қамтамасыз етеді;

ССҚаб –СС қабылдағышы.

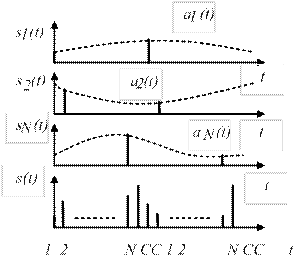
7.5-сурет –УББ қағидасының түсіндірмесі.

8 кездейсоқ шамалар мен олардың сипаттамалары

8.1 негізгі түсініктер

Реалды сигналдар мен кедергілер ықтималдықтар теориясы айналысатын кездейсоқ құбылыс болып табылады.

Кездейсоқ құбылыс – бір зерттеуді бірнеше рет қайталағанда әр түрлі болатын құбылыс. Оның 3 түрі болады:

- кездейсоқ оқиға;

- кездейсоқ шама;

- кездейсоқ процесс.

Сигналды математикалық сипаттағанда екі есепті шешуіміз қажет:

- кездейсоқ оқиғаның қай түріне кездейсоқ сигналды жатқызуға болатынын анықтау;

- қажетті статистикалық сипаттамаларды анықтау.

8.2 кездейсоқ оқиға

Кездейсоқ оқиға – тәжірибе кезінде орындалу немесе орындалмауы мүмкін кез келген факт.

Мысалы: оқ ату кезіндегі дәл түсу, тиынды лақтырғанда гербтің түсуі, тексттің қатесіз тасымалдануы, берілген деңгейді кедергімен асып түсу. Кездейсоқ оқиғалар латынның үлкен әріптерімен таңбаланады (А, В, С).

Оқиғаларды өзара алыстыру үшін цифрлы сипаттамалар қолданылады:

-оқиғаның пайда болу жиілігі;

- оқиға ықтималдығы.

Оқиғаның пайда болу жиілігі 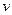– А оқиғасы пайда болған 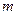тәжірибелер санының 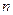жалпы тәжірибе санына қатынасы.:

.

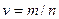Оқиға ықтималдығы 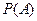– біртекті тәжірибелер санының шексіз өсуі кезіндегі оның пайда болу жиілігі

.

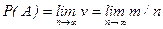Егер оқиға болған тәжірибелер саны 20-дан асса, кездейсоқ оқиғаның жиілігі саны жағынан оның ықтималдығымен сәйкес келеді деп санауға болады.

8.3 Кездейсоқ шама

Кездейсоқ шама – мәні әр тәжірибе сайын өзгеріп отыратын шама.

Мысалы: үш рет оқ ату кезіндегі түсу саны, тексттегі қате саны, арнадағы кедергі деңгейі. Кездейсоқ шамалар латынның үлкен әріптерімен таңбаланады(X, Y, Z), ал олар қабылдайтын мәндер - кіші әріптермен (x, y, z).

Кездейсоқ оқиғалар дискретті және үздіксіз болып бөлінеді. Дискреттілері тек бөлек, изоляцияланған алдын ала өлшеп қоюға болатын мәндерді қабылдайды.

Мысал: үш рет оқ атудағы түсу саны(0, 1, 2, 3 болуы мүмкін).

Үздіксіздері белгілі аралықты үздіксіз толтыратын мәндерді қабылдайды.

Мысал: оқ атудағы түсу нүктесінің абсциссасы ([ 0, r ] интервалында кез келген болуы мүмкін,мұндағы r – нысана радиусы).

Кездейсоқ оқиғаларды математикалық сипаттау үшін статистикалық сипаттамалар енгізіледі:

-ықтималдықты тарату функциясы;

-ықтималдықты тарату тығыздығы;

- математикалық күтім;

- дисперсия.

Ықтималдық тарату функциясы 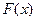–белгілі 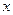мәнінен аспайтын кездейсоқ шамалардің барлық мәндерін көрсететін функция:

.

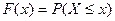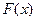жалпы ерекшеліктері:

- кемімейді (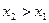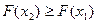болса);

- мәндері [0, 1] (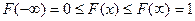) диапазонында жатады.

Егер 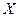- дискретті кездейсоқ шама болса, 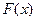- дискретті функция. Егер 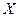- үздіксіз кедейсоқ шама болса, 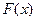- үздіксіз функция;

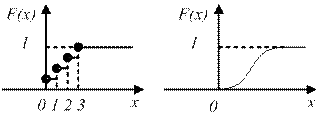
8.1-сурет – 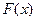дискретті және үздіксіз шамалар үшін графиктер.

Ықтималдық тарату тығыздығы 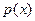тарату функциясының туындысы болып табылады:

.

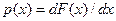Ол көптеген тәжірибелердегі кездейсоқ түрлі мәндердің пайда болу жиілігін сипаттайды. 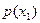функциясы неғұрлым көп болған сайын, 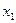-ке жақын кездейсоқ 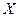шамасының мәндері соғұрлым көп пайда болады.

Ол тек үздіксіз кездейсоқ шамалар үшін қызмет етеді.

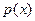және 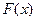ара қатынасы анықталады:

.

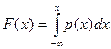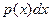туындысы кездейсоқ 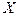шамасының түсу ықтималдығын сипаттайды:

.

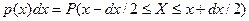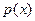негізгі қасиеттері:

- теріс емес ();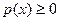

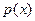- қисығының ауданы әрқашан 1-ге тең ();

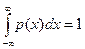8.2-сурет – 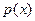графигі.

Дискретті кездейсоқ шама үшін ықтималдық тарату тығыздығының орнына ықтималдық тарату ұғымы енгізіледі.

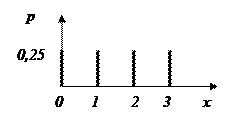
8.3-сурет –дискретті кездейсоқ шаманың ықтималдық таратуының графигі.

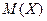немесе математикалық күтімі кездейсоқ шаманың орташа мәні болып табылады. Егер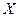– кездейсоқ кернеу (ток) болса, онда 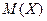- кернеудің(токтың) орташа мәні немесе тұрақты құраушысы болады.

Егер 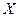- дискретті кездейсоқ шама болса, онда математикалық күтімді есептуде соммалау қолданылады:

,

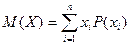мұндағы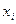-кездейсоқ шаманың мәндері;

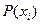-осы мәндердің ықтималдығы.

Егер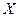-кездейсоқ үздіксіз шама болса, онда математикалық күтімді есептегенде интеграциялау қолданылады:

.

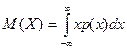Дисперсия 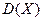немесе 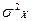бөлек тәжірибелердің лақтырылуының орташа мәнге салыстырмалы деңгейін сипаттайды. Егер 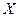– кездейсоқ кернеу(ток) болса, онда 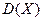- кернеудің (ток) ауыспалы құраушысының қуаты болады.

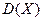кездейсоқ шаманың квадратының оның орташа мәніне ауытқуының математикалық күтімі ретінде есептелінеді.дискретті және үздіксіз шамалар үшін:

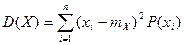и .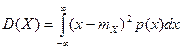

Дисперсияның түбір асты ортаквадраттық ауытұу деп аталады:

.

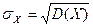8.4 Таратудың нормалды заңы

Таратудың нормалды заңы (гаусс) анализ үшін өте ыңғайлы.

Нормалды кездейсоқ шаманың тарату тығыздығы келесідей табылады:

,

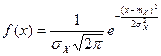Мұндағы және 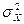- сәйкесінше математикалық күтім және дисперсия.

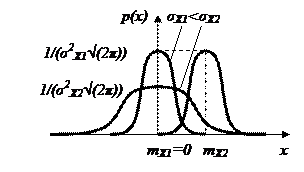
8.4 -сурет–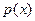кездейсоқ шамалардың нормалды таратылғандағы графигі.

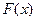графигі монотонды 0-ден 1-ге қарай өсетін қисықты береді.

F(x) 1 0,5

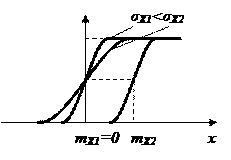
8.5 –сурет - 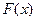кездейсоқ шамалардың нормалды тартудағы графигі.

10 байланыс арналарының жіктелуі және сипаттамалары

Электрбайланыс техникасының негізгі ұғымы болып электрбайланыс арнасы табылады.

Электрбайланыс арнасы – электрбайланыс біріншілік сигналдарын хабар түрлендіргіштен біріншілік сигнал жасаушыдан біріншілік сигналды хабарға түрлендіргішке тасымалдануын қамтамасыз ететін техникалық құралдар мен тарату ортасының кешені.

10.1 Байланыс арналарының жіктелуі

1.тасымалданатын біріншілік сигналдардың түріне қарай:

- телеграфтық;

- телефондық;

-дыбыстық;

- телевизиялық;

-мәліметтерді тасымалдау болып бөлінеді.

2. арнаның кірісі мен шығысындағы сигналдың сипатына қарай:

- дискретті;

- үздіксіз (аналогты);

- дискретті-үздіксіз немесе үздіксіз-дискретті.

3. арналық сигналдардың ажырау тәсіліне қарай:

- ажыратудың жай тәсілдерімен.

Мысал: теңселмейтін көпір тәсілімен ажырату.

- ажыратудың күрделі тәсілдері көмегімен.

Мысал: сызықты ажыратумен (уақыттық, жиіліктік ажырату көмегімен); сызықты емес ажыратумен (деңгей бойынша, комбинациялық ажырату).

4. алатын жиілік жолағына қарай:

- таржолақты. Мысал: тоналды жиілік арнасы(300…3400 Гц);

- кеңжолақты.

Мысал: телевидение кескіндерін тасымалдау арнасы(50…6500000 Гц).

5. Электрбайланыс сигналдарының таралу ортасына қарай:

- тасымалдауыш байланыс.

- радиобайланыс.

6. Арнаның кірісі мен шығысындағы сигналдардың ара қатынасы бойынша:

- детерленген ара қатынаспен;

- ықтималды ара қатынаспен

10.2 Байланыс арналарының сипаттамалары

Байланыс арналары 3 параметрмен сипатталады:

- Т_к қолдану уақытымен

- динамикалық диапазонмен D_к;

- ΔF_к өткізу жолағымен.

Арнаның 3 параметрінің көбейтіндісі оның сыйымдылығы деп аталады:

V_k=T_kD_kΔF_k.

Сигналдың арнамен үйлесу шарты

V_c≤V_k.

Жай түрінде сигнал арнаның барлық параметрлері бойынша сәйкестендіріледі:

T_c≤T_k, D_c≤D_k, ΔF_c≤ΔF_k.

11 Арнадағы кедергілер мен бұрмаланулар

Арнаның шығысындағы сигнал тасымалданған сигналдан кедергілер мен бұрмаланулар есебінен айырмашылық жасайды, сол себепті хабар кейбір қателермен келеді.

11.1 арнадағы бұрмаланулар

Бұрмалану – сигналдың формасын арнаның айқын сипаттамаларымен шартталған өзгерулері.

Бұрмаланудың келесі түрлері бар:

- сызықты. Сызықты бұрамаланулар амплитуда-жиіліктік және фаза-жиіліктік болып бөлінеді. Амплитуда-жиіліктік бұрмаланулар себебі болып амплитудалардың арасындағы қатынас бұзылуы, ал фаза-жиіліктікте – кіріс сигналдың спектрімен шығыс сигналдың спектрімен салыстырғандағы гармоникалық құраушылардың бастапқы фазалары. Бұл бұрмаланулар арнаның амплитуда-жиіліктік және фаза жиіліктік сипаттамаларының пішінімен анықталады;

- сызықты еместер. Сызықты емес бұрмаланулардың себебі болып кіріс сигналында болмаған гармоникалық құраушылардың гармоникалық құраушылардың шығыс сигналдың спектрінде пайда болуы табылады. Сызықты емес бұрмаланулар үлкендігін сигналдың амплитудалық сипаттамасы бойынша анықтауға болады.

11.2 Арнадағы кедергілер

Кедергі – қабылданған сигналдың жіберілген сигналға кездейсоқ ауытқушылық жасайтын, сигналға кедергі келтіретін кез келген әрекет.

1.кедергінің пайда болу жеріне қарай:

- сыртқы (байланыс арнасынан тыс):

- атмосфералық.жердегі атмосферадағы электрлік құбылыстармен байланысты. Көздері:найзағай разрядтары, полярлы жарқыраулар.

-ғарыштық.жерден тыс нысандардағы электромагниттік құбылыстармен байланысты. Көздері: Күн, жұлдыздар, жұлдызаралық газдар;

-өнеркәсіптік. Адамның іс-әрекетімен байланысты. Көздері:өнеркәсіптік, медициналық қондырулар, электротранспорт;

-бөгде байланыс құралдарынан;

- ішкі (арнаның өзінде болады). Көздері: жылулық шуыл және бөлінген шуыл.

2. Сигналға әсер ету сипаты бойынша:

- аддитивті – мәндері сигналдардың лездік мәндерінің қосындысы болып табылатын кедергілер:

,

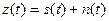Мұндағы 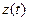-қабылданатын тербеліс;

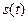-тасымалданатын сигнал;

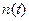- кедергі.

Сигнал жоқ болса да орын алады;

- мультипликативті – мәндері сигналдардың лездік мәндерімен көбейтілетін кедергілер:

.

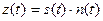Сигнал бар кезде ғана орын алады.

3.Пішіні бойынша кедергілер:

- флуктуациялық (уақыт және жиілік бойынша) – кездейсоқ түрде өзгеретін үздіксіз тербелістер.

Кедергілер спектрі аса үлкен;

- гармоникалық (жиілік бойынша)

- импульстік (уақыт бойынша)

Кедергілерр алдын ала белгісіз болғандықтан оларды толықтай жою мүмкін емес.

12 Хабар көздерінің ақпараттық сипаттамалары

12.1 мәліметтің цифрлы шамасы

Байланыс теориясы мен техникасында мәлімет көлемін анықтауда хабардың құрылымдық жағы ескерілмейді. Мәліметті өлшеу негізіне хабардың анық еместігінің деңгейін көрсететін ықтималдық сипаттамалары қойылған.

Ақпарат көлемі 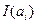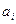бөлек алынған хабарының 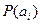хабар ықтималдығына кері шамамен алынады және логарифмдік бірліктерде қолданылады:

,

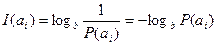Мұндағы 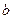-логарифм негізі. Ақпарат көлемі шама бірлігін:

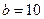- - ондық бірлік (дит);

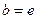- - натурал бірлік (нат);

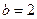- - екілік бірлік (бит).

1 БИТ – ықтималдығы 0,5 болатын хабардағы ақпарат көлемі. Мұндай бірлік практикада есептеуіш техника мен байланыста екілік кодалардың кең пайдалануы есебінен қолдану аса ыңғайлы.

Тәуелді хабарларда хабардағы ақпарат көлемі:

,

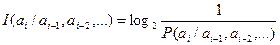мүндағы 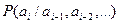- 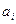хабардың шартты ықтималдығы, алдында 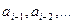болса.

12.2 дикретті хабар көздерінің ақпараттық сипаттамалары

Кей мүмкін хабарлар ансамблінен тізбекті беретін дискретті көзді қарастырайық 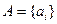, мұндағы 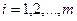, 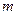- әліпби көлемі.

Кей әліпбиден 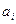хабар тізбегін көрсететін дискретті хабар көзін қарастырайық.

Дискретті көзбен берілетін ақпараттың орташа көлемі көздің энтропиясы деп аталады:

, .

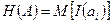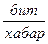Тәуелсіз хабар көздері үшін:

.

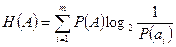Шартты энропия ұғымы:

,

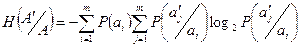Мұндағы 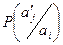- 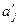пайда болу ықтималдығы, алдында 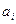болған жағдайда.

Энтропияны көздің әрекетіндегі анықталмағандық шарасы ретінде қарастырамыз.

Энтропияның негізгі қасиеттері:

-дискретті хабарлар үшін ол –заттық, шектелген және оң ұғым;

- бір символ ықтималдығы 1 болып таңдалса 0-ге тең болады;

- максималды, егер көздің символдары тәуелсіз және бірдей ықтималдықпен пайда болса:

Дата добавления: 2014-10-31