Типовые звенья

Динамическим звеном называют устройство любого физического вида и конструктивного оформления, представленное определенным дифференциальным уравнением.

В соответствии с определением классификация динамических звеньев производится по виду дифференциального уравнения, а именно, по его порядку. Так как одними и теми же дифференциальными уравнениями могут описываться устройства любого типа (электрические, электромеханические, гидравлические, тепловые), то такое предположение позволяет использовать для проектирования различных устройств одинаковые подходы.

Любую систему можно представить в виде соединения типовых динамических звеньев. Число таких звеньев невелико и определяется типом нулей и полюсов.

Как следует из представления модели в форме пространства состо­яний, для реализации любой физически осуществимой передаточной функции достаточно двух типов звеньев: интеграторов и усилителей. Если степень числителя передаточной функции m превышает степень знаменателя n, то необходимо звено дифференцирующего типа.

В теории управления состав типовых звеньев несколько расширен, исходя из соображения удобства, необходимы звенья, моделирующие часто встречающиеся случаи, а также позволяющие представление пе­редаточных функций общего вида последовательным и параллельным соединением типовых звеньев.

Большинство сиcтем может быть представлено совокупностью относительно звеньев с передаточными функциями невысокого порядка. Такие звенья называются типовыми.

Типовым называется такое звено, которое описывается дифференциальным уравнением не выше второго порядка. К таким звеньям относятся:

· безынерционное звено – звено нулевого порядка,

· апериодическое звено – звено первого порядка,

· интегрирующее звено – звено первого порядка,

· дифференциальное звено – звено первого порядка,

· колебательное звено – звено второго порядка.

3.8.1. Безынерционное звено

Уравнение движения для безинерционного звена имеет вид

.

Выполняя над этим уравнением преобразование Лапласа получаем выражение для передаточной функции звена следующего вида:

Для нахождения временных характеристик звена определим его реакцию на единичное ступенчатое воздействие. Изображение переходной функции определяется как

.

Выполняя обратное преобразование изображения переходной характеристики 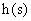, получаем:

Выполняя аналогичные преобразования над изображением весовой функции, получаем выражение для определения весовой функции .

Для построения частотных характеристик звена воспользуемся выражением для его комплексной передаточной функцией вида:

Исходя из этого, амплитудно-частотная характеристика звена представляется точкой на комплексной плоскости.

Логарифмическая частотная характеристика представляется прямой параллельной оси частот. Это следует из выражения для определения логарифмической частотной характеристики вида:

.

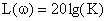3.8.2. Апериодическое звено

Уравнение движения для безинерционного звена имеет вид

.

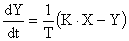Выполняя над этим уравнением преобразование Лапласа получаем выражение для передаточной функции звена следующего вида:

Для нахождения временных характеристик звена определим его реакцию на единичное ступенчатое воздействие. Изображение переходной функции определяется как

.

Корни характеристического уравнения определяются как

.

Выполняя обратное преобразование изображения переходной характеристики 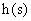получаем:

.

Выполняя аналогичные преобразования над изображением весовой функции

получаем выражение для определения весовой функции .

Переходная и весовая характеристики звена приведены на рис. 3.27.

Рис. 3.27

Для построения частотных характеристик звена воспользуемся выражением для его комплексной передаточной функцией вида:

Исходя из этого, амплитудно-частотная характеристика звена определяется как:

.

Вещественная 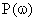и мнимая 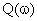частотные характеристики звена определяются как

АФЧХ звена определяется как

Выражение для расчета ЛАЧХ принимает вид:

.

.

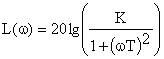Для построения асимптотической ЛАЧХ воспользуемся выражением вида:

.

На рис. 3.28 приведены амплитудно-фазовая и логарифмическая частотные характеристики безинерционного звена.

Рис. 3.28

Дата добавления: 2014-10-31