Метрические задачи

Следует отметить, что выступающие углы треугольника всегда видимые.

Положение точки относительно плоскостей проекций. Точка принадлежит плоскости, если проекции точки лежат на соответствующих проекциях прямой, принадлежащих данной плоскости. Если точка лежит в плоскости проекций, то ее проекция на эту плоскость совпадает с самой точкой, а две другие проекции располагаются на осях проекций (рис. 21).

с

Две проекции точки, лежащие на оси проекций, совпадают с самой точкой, а третья находится в начале координат.

с

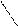
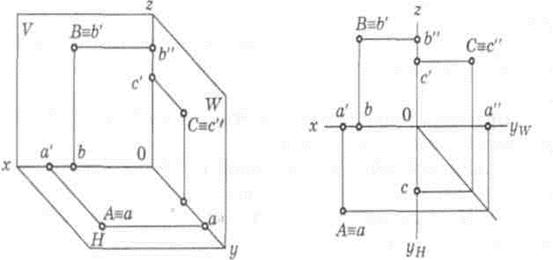
Рис. 21. Проекции точек, лежащих на плоскостях проекций

Нахождение натуральной величины треугольника способом перемены плоскостей. Введем две дополнительные плоскости проекций (рис. 22):

1. V₁ H и V₁ ABC.

2. H₁ V₁ и H₁ ABC.

n₂

l₃

l₁

n₃

n₁

l₂

Рис. 22. Определение натуральной величины треугольника способом перемены плоскостей

1. Так как V₁ H и V₁ ABC, то ABC является проецирующим в плоскости V₁. Для построения проекции ABC в плоскости V₁ построим горизонталь (А1): ее фронтальная проекция (a’1’), горизонтальная проекция (a1).

2. Перпендикулярно горизонтальной проекции (a1) проведем ось X₁ — горизонтальный след плоскости V₁.

3. Проведем через точки a, b, c прямые l₁, l₂, l₃ 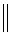(a1).

4. От оси X₁ на l₁, l₂, l₃ отложим отрезки z_A, z_B, z_C, которые должны лежать на одной прямой. Отрезок (c₁b₁) — фронтальная проекция ABC в плоскости V₁.

5. Рассмотрим плоскости H₁ V₁ и H₁ ABC, в ней ABC является треугольником уровня и виден в натуральную величину. Проведем ось X₂ 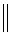(c₁b₁) — след плоскости H₁ в плоскости V₁.

6. Проведем через точки a₁, b₁, c₁ прямые n₁, n₂, n₃ X₂.

7. На прямых n₁, n₂, n₃ отложим от оси X₂ расстояния y_A, y_B, y_C и получим точки a₂, b₂, c₂.

8. a₂ b₂ c₂ является натуральной величиной ABC.

Нахождение натуральной величины треугольника способом вращения без указания на чертеже осей вращения, перпендикулярных плоскостям V и H. Порядок построения указан на рис. 23.

Рис. 23. Определение натуральной величины треугольника методом вращения

Поворот вокруг оси H, проходящей через точку a до положения ABC V.

1. В ABC проводим горизонталь (А1): в a’b’c’ проведем прямую (a’1’) 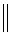X.

2. В abc найдем проекцию горизонтали (a1).

3. На свободном поле чертежа проведем прямую (a₁1₁) V, или, что то же самое (a₁1₁) X.

4. От точки a₁ сделаем засечку радиусом r₁, от точки 1₁ сделаем засечку радиусом r₂ и на пересечении получим точку b₁.

5. Проведем прямую через точки b₁ и 1₁ и на ней от точки 1₁ радиусом r₃ получим точку c₁.

6. Из точек a’, b’, c’ проведем прямые параллельно оси X, из точек a₁, b₁, c₁ проведем перпендикуляры к оси X, на их пересечении получаем точки a₁’, b₁’, c₁’. Отрезок (b₁’ c₁’) — фронтальная проекция ABC.

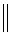Поворот вокруг оси V, проходящей через точку c₁ до положения ABC H.

1. Через точку c₁’ проведем прямую l 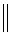X.

2. Радиусами (c₁’a₁’), (c₁’b₁’) сделаем засечки на прямой l и получим точки a₂’, b₂’.

3. Из точек a₂’, b₂’, c₁’ проведем прямые перпендикулярно X, из точек a₁, b₁ проведем прямые параллельно X, на их пересечении получим точки a₂, b₂.

4. a₂ b₂ c₁ — натуральная величина ABC.

Дата добавления: 2014-11-06