Многогранники

Геометрическая поверхность образуется движением в пространстве прямой или кривой линии, называемой образующей, по другой линии (или двум линиям) называемой направляющей. Часть пространства, ограниченная со всех сторон геометрической поверхностью, называется геометрическим телом.

Эпюры многогранников. Многогранником называется геометрическое тело, ограниченное плоскими фигурами — многоугольниками.

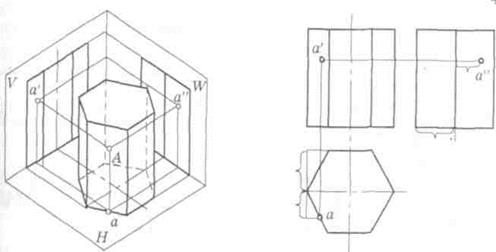
Призма — многогранник, две грани которого являются равными многоугольниками, расположенными в параллельных плоскостях (основания призмы), а остальные грани — параллелограммами (боковые грани призмы) — см. рис. 24.

Рис. 24. Эпюры шестигранной призмы

Призма, боковые грани которой перпендикулярны основаниям, называется прямой. Если боковые грани не перпендикулярны основаниям, призма называется наклонной. Боковые грани прямой призмы представляют собой прямоугольники. Если в основании прямой призмы лежит правильный многоугольник, то призма называется правильной. Линии пересечения боковых граней называются боковыми ребрами. Линии пересечения боковых граней с основаниями называются ребрами основания. Точки пересечения ребер называются вершинами призмы.

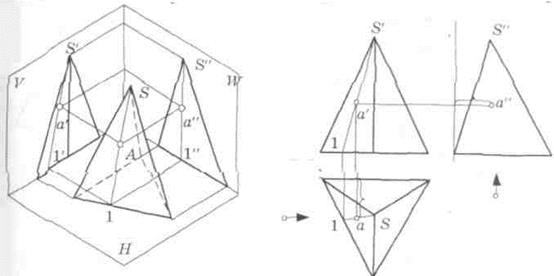
Пирамида — многогранник, одна грань которого (основание) является многоугольником, а остальные грани (боковые) — треугольники с общей вершиной (рис. 25).

Рис. 25. Эпюры трехгранной пирамиды

Если в основании пирамиды лежит правильный многоугольник, а высота пирамиды проходит через центр основания (центр описанной вокруг основания окружности), то пирамида называется правильной. Боковыми гранями правильной пирамиды будут равнобедренные треугольники. Боковые ребра пирамиды пересекаются в одной точке, называемой вершиной пирамиды.

Пересечение многогранников. Рассмотрим задачу определения линии пересечения призмы и пирамиды (рис. 26).

1. Найти точки пересечения ребер призмы с гранями пирамиды.

1.1. Так как грани призмы перпендикулярны к плоскости H, то горизонтальные проекции точек пересечения ребер пирамиды с гранями призмы: точки 1 = (as) (ek), 3 = (bs) (ek), 3 = (bs) 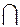(ed), 4 = (bs) 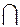(dk), 5 = (cs) 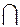(ed), 6 = (cs) 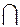(ek).

1.2. Найдем соответствующие фронтальные проекции полученных точек линиями проекционной связи: точки 1’ на (a’s’), 2’ на (a’s’), 3’ на (b’s’), 4’ на (b’s’), 5’ на (c’s’), 6’ на (c’s’).

2. Найти точки пересечения ребер призмы с гранями пирамиды.

2.1. Ребра EE₁ и DD₁, как видно из чертежа, в пересечении не участвуют.

2.2. Для построения точек пересечения ребра KK₁ с гранями пирамиды проведем через ребро KK₁ горизонтально-проецирующую плоскость, которая пересекает грань ABS по прямой (MS), грань BCS по прямой (NS): горизонтальный след этой плоскости — прямая (ms,ns), фронтальные проекции этого следа будут на соответствующих плоскостях -— это прямые (m’s’), (n’s’).

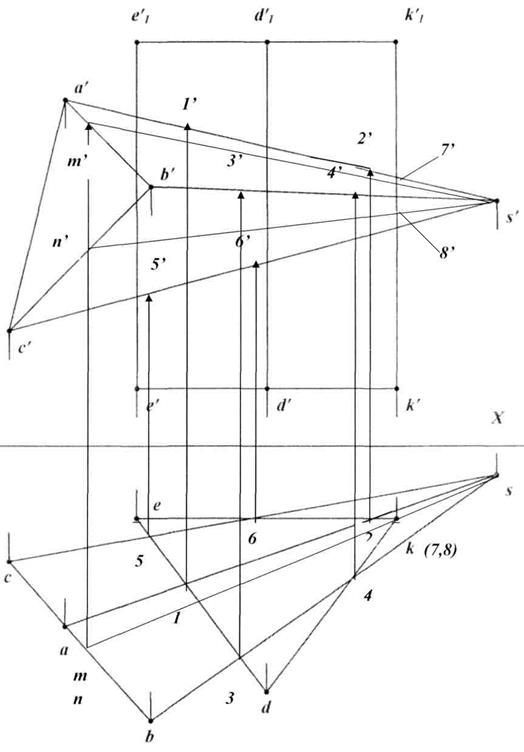2.3. Фронтальные проекции точек пересечения ребер призмы с гранями пирамиды: точки 7’ = (m’s’) 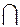(k₁’k’), 8’ = (n’s’) 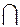(k₁’k’). Горизонтальные проекции точек пересечения ребер пирамиды с гранями призмы: точки 7 и 8.

	Рис. 26. Построение точек пересечения призмы и пирамиды

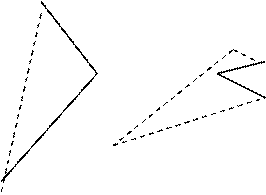
В данном случае горизонтальная проекция линии пересечения поверхностей многогранников совпадает с горизонтальной проекцией призмы, и найденные точки следует соединять только на фронтальной проекции. Для определения последовательности соединения фронтальных проекций точек, полученных в пересечении двух многогранников, используют метод Д.Г. Ананова. Он основан на построении схематических разверток поверхностей пересекающихся тел. Ребра призмы на схеме расположены вертикально, ребра пирамиды — наклонно (рис. 27). На развертки наносим точки, принадлежащие линии пересечения. Отметим на схеме знаком «+» те грани, которые на фронтальной плоскости будут видимы, а знаком «-» те грани, которые на этой плоскости будут невидимы. (Линии на гранях, где сочетаются два «минуса», будут невидимы).

Составляем схему соединения точек и видимости линий.

Рис. 27. Схема соединения точек и видимости линий

Соединим точки, лежащие на одной грани: точки 1 и 3, 3 и 5, 5 и 1 –— лежат на грани EDE₁D₁, точки 2 и 7, 7 и 4 — лежат на грани ABS, точки 4 и 8, 8 и 6 — лежат на грани CBS точки 6 и 2 — лежат на грани ACS.

Определим видимость, используя правило: отрезки, принадлежащие двум видимым граням, — видимы,; отрезки, принадлежащие двум невидимым граням, — невидимы;, отрезки, принадлежащие двум разным по видимости граням, — невидимы.

Отрезки 1-3, 3-5, 7-4, 4-8 — видимы,; отрезки 5-1, 2-7, 8-6, 6-2 — невидимы.

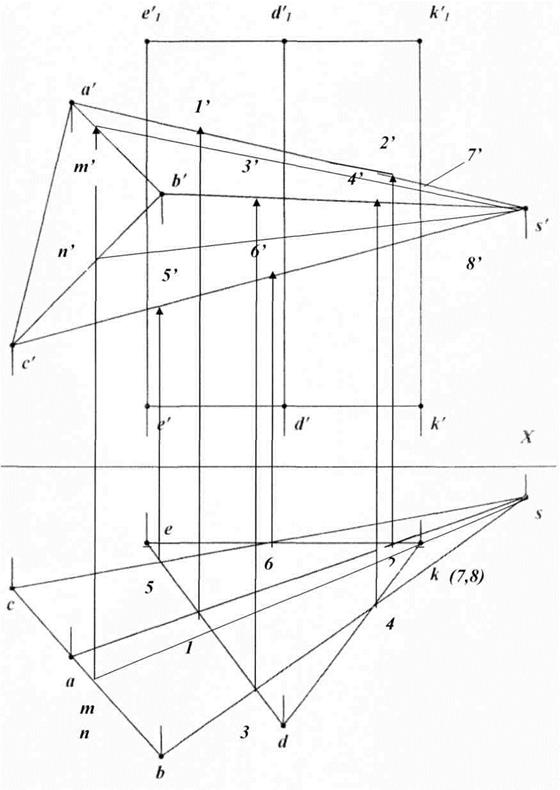
На фронтальной проекции соединим отрезки согласно схеме, видимые отрезки — сплошными основными линиями, невидимые — штриховыми линиями (рис. 28).

Рис. 28. Построение линий пересечения призмы и пирамиды

Рис. 28. Построение линий пересечения призмы и пирамиды

Дата добавления: 2014-11-06