Математическая обработка результатов испытаний

При определении какого-либо показателя свойства материала час­то приходится сталкиваться с тем, что значения, получаемые при из­мерении этого показателя, неодинаковы. Например, прочность кон­трольных кубов одного замеса бетона почти всегда неодинакова. Эти отклонения могут быть обусловлены разными причинами: не­точностью измерительных приборов или неправильностью методики измерений, ошибками работника, производящего измерения, и неизбежными отклонениями свойств самого материала.

Первые две причины, называемые систематические ошибки, могут быть устранены или учтены. Третья причина – случайные ошибки, которые складываются из множества неконтролируемых причин: не­однородности материала, различием в его технологической обработке и т.п. Полностью исключить влияние случайных ошибок невозмож­но. Эти ошибки вызывают отклонения при измерении в обе стороны от истинного значения. Эти отклонения обычно подчиняются нор­мальному закону распределения:

– отклонения не могут иметь один и тот же знак, т.е. измеряемые значения бывают и больше, и меньше среднего значения;

– абсолютные значения отклонений ограничены какими-либо пре­делами для большинства результатов измерений;

– чем больше значение отклонения, тем реже оно встречается;

– если число измерений достаточно велико, то сумма положитель­ных отклонений приблизительно равна сумме отрицательных.

Ряд числовых значений, полученных при измерении, называют рядом измерений или статистической совокупностью. Например, при определении прочности бетона партии бетонных изделий полу­чены следующие значения (МПа): 21,0; 22,4; 21,4; 21,6; 25,6. Прос­тейший способ оценки прочности бетона в данной партии – опре­деление средних значений.

Среднее арифметическое значение – статистическая характерис­тика, описывающая одним числом результаты некоторого ряда изме­рений. Среднее арифметическое значение Х вычисляют по формуле

,

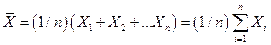где Х ₁, Х ₂, … Х_п, – результаты отдельных измерений; п – число из­мерений.

Для данного примера сумма результатов всех измерений – 112 МПа, число измерений п = 5. Среднее арифметическое значение прочности (средняя прочность) бетона в данной партии 22,4 МПа.

Среднее арифметическое дает представление о среднем значении измеряемой величины, но ее изменчивости, т.е. пределов колебания (варьирования) этой величины, не отражает. Так, при определении прочности бетона в двух партиях изделий прочность бетона оказалась (МПа): в первой партии – 21,0; 22,4, 21,4; 21,6; 25,6; во второй пар­тии – 19,0; 24,4; 20,1; 23,0; 25,5. Средняя прочность в обеих партиях бетона 22,4 МПа, но колебания прочности во второй партии значи­тельно больше, чем в первой.

Среднее квадратичное отклонение S служит характеристикой средней изменчивости изучаемой величины. Его выражают в тех же единицах, что и среднее арифметическое значение, и вычисляют по формуле

,

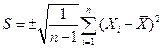где 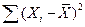– сумма квадратов отклонений всех измерений от среднего арифметического; п – число измерений.

Знак плюс или минус в формуле показывает, что отклонение мо­жет быть как в одну, так и в другую сторону от среднего арифме­тического.

Квадрат среднего квадратичного отклонения S ² называется дис­персией.

На практике для характеристики разброса измерений часто ис­пользуют понятие размах (варьирование) R, который представляет собой разность между максимальным и минимальным значениями в ряду измерений,

R = X _max – X _min.

Так, для первой партии бетона

r ₁ =25,6 – 21,0= 4,6 МПа,

а для второй –

R ₂= 25,5 – 19= 6,5 МПа.

Размах используют главным образом при анализе результатов не­большого числа измерений (до 10), чтобы облегчить вычисление среднего квадратичного отклонения, которое вычисляют по формуле

S= (X _max – X _min)/ d, (4.16)

где d – коэффициент, зависящий от числа измерений:

п
d	1,13	1,69	2,06	2,33	2,53	2,70	2,85	2,97	3,08

Например, для 1-й и 2-й партий бетона при числе измерений п = 5 d = 2,33. Тогда среднее квадратичное отклонение, вычисленное по вышеприведенной формуле, будет следующим:

S ₁ = (25,6 – 21,0)/2,33 = 1,97 МПа;

S ₂ = (25,5 – 19,0)/2,33 = 2,79 МПа.

При обработке опытных данных при п 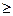10 среднее квадратичное отклонение рассчитывают по формуле (4.15). Для удобства вычисле­ний используют таблицу, составленную из трех граф. В первой графе, обозначенной X, записывают полученные результаты; во второй, обо­зна­чен­ной Δ, – отклонения отдельных результатов (со знаком плюс или минус) от среднего арифметического 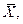в третьей, обозна­ченной Δ², – квадраты этих отклонений (со знаком плюс). Необ­ходимо помнить, что сумма отклонений Δ со знаком плюс должна быть равна сумме отклонений со знаком минус.

Среднее квадратичное отклонение – одна из наиболее важных статистических характеристик. Однако его абсолютное значение не позволяет сравнить степень изменчивости изучаемого свойства у не­скольких групп материалов. Например, в результате испытаний двух партий бетона на сжатие получено 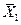= 45,0 МПа, S ₁ = 6 МПа
и 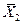= 12,2 МПа, S ₂ = 2,9 МПа. Сравнивая абсолютные значения сред­него квадратичного отклонения, можно сделать вывод, что предел прочности при сжатии первой партии более изменчив, чем второй. Но если оба средних квадратичных отклонения выразить в процентах от соответствующих им средних арифметических, то для первой пар­тии получим

(S ₁/ 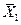)100 % = 3,3 %,

а для второй –

(S₂ / 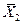)100 % = 23,8 %,

т.е. относительная изменчивость у второй партии больше, чем у первой. Показатель относительной изменчивости ν (%), назы­ваемый коэффициентом вариации, вычисляют по формуле

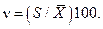
При обработке экспериментальных данных в некоторых случаях отдельные результаты измерений имеют значительно большее от­клонение от среднего, чем остальные. В подобных случаях прежде всего проверяют, не допущена ли ошибка в процессе экспериментального определения. Если удается точно установить причину такого отклонения, то результат необходимо исключить из расчетов.

Однако бывают случаи, когда не удается установить причину зна­чительного отклонения числа, а подозрения в его ошибочности ос­таются. В таком случае проверяют принадлежность подозреваемого числа к исследуемому статистическому ряду. В стандартах эта опера­ция называется проверка анормальности. Результаты испытаний принимают анормальными и не учитывают в дальнейших расчетах, если относительное отклонение T _к, определяемое по формуле T _к = (X – 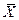)/ S, не пре­вышает допустимых значений, указанных ниже:

Число результатов испытаний
T к	1,15	1,46	1,67	1,82	1,94	2,03	2,11	2,18

При наличии в ряду измерений двух подозреваемых в грубой оши­бочности чисел первоначально проверку делают для более резко отклоняющегося значения; и уже после исключения его – для второго.

Краткое содержание главы

Структурные характеристики и свойства строительных материалов принято разделять на основные, одинаково важные для всех строи­тельных материалов (например, плотность, пористость, прочность), и специальные, позволяющие оценить возможность применения дан­ного материала для определенных целей (например, водонепроницае­мость, огнеупорность).

В соответствии с возможными воздействиями на материал струк­турные характеристики и свойства строительных материалов класси­фицируют на:

– структурные характеристики – плотность, пористость, дисперс­ность и другие;

– физические свойства, определяющие отношение материала к раз­личным физическим процессам и воздействиям, – влажность, водопоглощение, морозостойкость, теплопроводность, электро­проводность и т.п.;

– механические свойства, определяющие отношение материала к деформирующему и разрушающему действию механических нагру­зок, – прочность, твердость, истираемость и другие;

– химические свойства, характеризующие способность материала к химическим превращениям и стойкость против химической кор­розии;

– долговечность – комплексный показатель, связанный с изменени­ем главнейших эксплутационных свойств материалов во времени.

Свойства материалов оценивают числовыми показателями, уста­навливаемыми путем испытаний по стандартной методике.

Плотностью называется масса единицы объема материала. Чтобы вычислить плотность 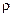(кг/м³), надо знать массу материала т (кг) и его объем V (м³):

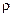= m / V.

Пористость – степень заполнения объема материала порами. Ис­ходя из определения, пористость П (%) можно рассчитать по сле­дующей формуле:

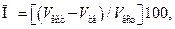
где V _ест – объем материала в естественном состоянии, см³; V _тв – объ­ем материала в абсолютно плотном состоянии (т.е. объем твердого вещества в материале).

На практике пользуются другой формулой. Если естественный объем материала V _ест и объем твердого вещества в нем V _тв, выразить через массу материала т и среднюю ρ _m и истинную ρ плотности: V _ест = m /ρ _m V _тв = m /ρ, то формула для расчета пористости (%) примет вид

П = [(m /ρ _m – m /ρ/(m /ρ _m)]100 = [(ρ – ρ _m)/ρ]100.

Строительные материалы в процессе их эксплуатации и хране­ния могут поглощать влагу. При этом их свойства существенно из­меняются. Так, при увлажнении материала повышается его тепло­проводность, изменяются средняя плотность, прочность и другие свойства.

Многие строительные конструкции (стены и фундаменты зданий, устои мостов, покрытия дорог) подвергаются совместному действию влаги и знакопеременных температур, которые постепенно приводят их к разрушению. Причина разрушения – расширение (примерно на 9 %) воды при замерзании в порах материала.

При определении механических свойств строительных материалов используют законы сопротивления материалов – науки о прочности и деформативности материалов и конструкций.

При определении прочности строительных материалов образец материала доводят до разрушения. Задача таких испытаний – определение напряжения, ниже которого материал существует неограниченно долго, а выше которого – разрушается мгно­венно. Это предельное напря­жение называется пределом прочности материала и обозна­чается R. Предел прочности рас­считывают по тем же формулам, что и напряжения, но вместо действующей силы берут силу разру­шающую P _p.

Прежде чем приступить к испытанию образцов на прочность, определяют, какой мощности пресс необходимо приме­нять. В основу выбора положено правило: нагрузка, разрушающая образец, должна составлять не менее 0,2 и не более 0,8 от предельной нагрузки Р _maxпресса (при заданной шкале измерения нагрузки). При разрушающей нагрузке, меньшей 0,2 Р _max, точность измерения на­грузки снижается, а при нагрузках, близких к 0,8 Р _max, трудно обес­печить необходимую скорость нагружения, а детали и гидравлическая система пресса подвергаются повышенному изнашиванию. Разру­шающую нагрузку рассчитывают ориентировочно, исходя из пас­портных данных на материал и размеров испытуемых образцов.

Для определения прочности строительных материалов на изгиб применяют разнообразные машины и приборы. Каменные материалы (в том числе бетон) при определении прочности на изгиб требуют значительно меньших усилий, чем при определении прочности на сжатие.
Поэтому при испытании на изгиб могут быть использованы прессы малой мощности, снабженные специальными приспособле­ниями для установки образцов и передачи нагрузки, и универсальные испытательные машины. Для определения прочности на изгиб вяжущих веществ в виде стандартных образцов-балочек размером 40´40´160 мм применяют прибор Михаэлиса и машину МИИ-100, а также универсальные испытательные машины, оснащенные приспо­соблениями для испытания на изгиб.

Истираемость строительных материалов определяют специаль­ными приборами, конструкция которых зависит от вида материала. Так, полимерные материалы для полов испытывают на машине МИВОВ-2 с помощью шлифовальной шкурки, а каменные материалы (бетоны, растворы, природный камень, керамическую плитку) на кругах истирания с использованием шлифовальных по­рошков (кварцевый песок).

Твердость каменных строительных материалов оценивают по шка­ле твердости Мооса (см. табл. 4.2), которая составлена из десяти минера­лов, расположенных по степени нарастания твердости.

При всех методах измерения значения твердости являются услов­ными, зависящими не только от свойств материала, но и от метода испытания. Поэтому для сравнения твердости различных образцов их испытание проводят каким-либо одним методом.

Некоторые строительные материалы – растворные и бетонные смеси, мастики, краски и др. – представляют собой пастообразные массы различной густоты. Чтобы такие материалы плотно уклады­вались в форму (опалубку) или хорошо сцеплялись с поверхностью конструкции, не сползая (не стекая) с нее, они должны обладать оп­ределенными свойствами. Для оценки таких свойств используют рео­логические методы и приборы.

Реология – наука о деформациях и текучести веществ. Объект реологии – жидкие и пластичные вещества. Жидкостями в реологии считаются вещества, которые под действием приложенной силы не­ограниченно деформируются, т.е. текут. Твердые тела (идеальные), напротив, под действием силы деформируются обратимо (упруго) и восстанавливают свою форму после окончания действия силы. Ре­альные материалы, в том числе бетонные и растворные смеси, мастики, краски, сочетают в себе свойства жидких и твердых тел. В зави­симости от преобладания того или иного свойства говорят о вязкотекучих или пластично-вязких смесях.

К основным реологическим характеристикам относятся вязкость, предельное напряжение сдвига, тиксотропия.

При определении какого-либо показателя свойства материала час­то приходится сталкиваться с тем, что значения, получаемые при из­мерении этого показателя, неодинаковы. Например, прочность кон­трольных кубов одного замеса бетона почти всегда неодинакова. Эти отклонения могут быть обусловлены разными причинами: не­точностью измерительных приборов или неправильностью методики измерений, ошибками работника, производящего измерения, и неизбежными отклонениями свойств самого материала.

Первые две причины, называемые систематические ошибки, могут быть устранены или учтены. Третья причина – случайные ошибки, которые складываются из множества неконтролируемых причин: не­однородность материала, различия в его технологической обработке и т.п. Полностью исключить влияние случайных ошибок невозмож­но. Эти ошибки вызывают отклонения при измерении
в обе стороны от истинного значения. Эти отклонения обычно подчиняются нор­мальному закону распределения:

– отклонения не могут иметь один и тот же знак, т.е. измеряемые значения бывают и больше, и меньше среднего значения;

– абсолютные значения отклонений ограничены какими-либо пре­делами для большинства результатов измерений;

– чем больше значение отклонения, тем реже оно встречается;

– если число измерений достаточно велико, то сумма положитель­ных отклонений приблизительно равна сумме отрицательных.

Дата добавления: 2014-11-25