Равновесие произвольной пространственной системы сил

Для выполнения условий (1.25) требуется, чтобы 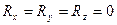и 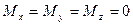, т.е.

, , ; , ,

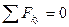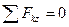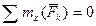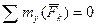(1.33)

Т. о., для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы алгебраическая сумма проекций всех этих сил на каждую из трех любым образом выбранных координатных осей равнялась нулю и чтобы алгебраическая сумма их моментов относительно каждой из этих осей также равнялась нулю.

Условия (1.33) называются условиями равновесия произвольной пространственной системы сил в аналитической форме.

Условия равновесия пространственной системы параллельных сил. Если линии действия всех сил данной системы сил расположены в разных плоскостях и параллельны между собой, то такая система сил называется пространственной системой параллельных сил.

Пользуясь условиями равновесия (1.33) произвольной пространственной системы сил, можно найти условия равновесия пространственной системы параллельных сил. (Выведенные нами ранее условия равновесия для плоской и пространственной систем сходящихся сил, произвольной плоской системы сил и плоской системы параллельных сил также можно было бы получить, пользуясь условиями равновесия (1.33) произвольной пространственной системы сил).

Пусть на твердое тело действует пространственная система параллельных сил (рисунок 1.26). Так как выбор координатных осей произволен, то можно выбрать координатные оси так, чтобы ось z была параллельна силам. При таком выборе координатных осей проекции каждой из сил на оси х и у и их моменты относительно оси z будут равны нулю, и, следовательно, равенства , 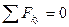и удовлетворяются независимо от того, находится ли данная система сил в равновесии или нет, а поэтому перестают быть условиями равновесия. Поэтому система (1.33) даст только три условия равновесия:

; , ,

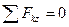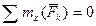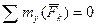(1.34)

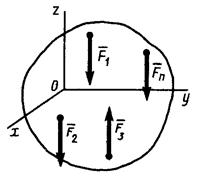
Рисунок 1.26 – Удобное расположение осей координат для пространственной системы параллельных сил

Следовательно, для равновесия пространственной системы параллельных сил необходимо и достаточно, чтобы алгебраическая сумма проекций всех сил на ось, параллельную этим силам, равнялась нулю и чтобы алгебраическая сумма их моментов относительно каждой из двух координатных осей, перпендикулярных к этим силам, также равнялась нулю.

При решении задач статики рекомендуется придерживаться следующего порядка:

1. Выбрать тело (или точку), равновесие которого должно быть рассмотрено в данной задаче.

2. Освободить выбранное тело от связей и изобразить (расставить) все действующие на это тело (и только на это тело) активные силы и силы реакций отброшенных связей. Тело, освобожденное от связей, с приложенной к нему системой активных сил и сил реакций, следует изображать отдельно.

3. Составить уравнения равновесия. Для составления уравнений равновесия необходимо сначала выбрать оси координат. Этот выбор можно производить произвольно, но полученные уравнения равновесия будут решаться проще, если одну из осей направить перпендикулярно к линии действия какой-либо неизвестной силы реакции. Решение полученных уравнений равновесия следует, как правило, проводить до конца в общем виде (алгебраически). Тогда для искомых величин будут получаться формулы, позволяющие проанализировать найденные результаты; численные значения найденных величин подставляются только в окончательные формулы. Уравнения равновесия составляются при аналитическом методе решения задач на равновесие системы сходящихся сил. Однако, если число сходящихся сил, равновесие которых рассматривается, равно трем, то удобно применить геометрический метод решения этих задач. Решение в данном случае сводится к тому, что вместо уравнений равновесия всех действующих сил (активных и реакций связей) строится силовой треугольник, который на основании геометрического условия равновесия должен быть замкнут (начинать построение этого треугольника следует с заданной силы). Решая силовой треугольник, находим искомые величины.

Дата добавления: 2014-11-25