Скорость точки

Координатный способ задания движения точки.

Аналитически, как известно, вектор задается его проекциями на координатные оси. Для вектора будет:

и ,

(2.2)

где 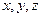– координаты точки. Тогда, если ввести единичные векторы (орты) координатных осей, получим для вектора выражение

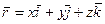
(2.3)

Следовательно, зависимость 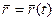будет известна, если будут заданы координаты 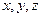точки как функции времени. Такой способ задания движения точки (координатный) рассмотрим ниже.

Чтобы знать закон движения точки, т.е. её положение в пространстве в любой момент времени, надо знать значения координат точки для каждого момента времени, т.е. знать зависимости

, ,

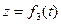
(2.4)

Эти уравнения и есть уравнения движения точки в прямоугольных декартовых координатах. Они определяют закон движения точки при координатном способе задания движения.

Эти уравнения можно рассматривать как параметрические уравнения траектории точки. Исключим параметр t. Для этого можно, например, найдя t =φ(x), подставить в и 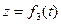,а затем сложить эти уравнения. Получим уравнение траектории в координатной форме.

Если движение происходит в одной и той же плоскости, то, приняв эту плоскость за плоскость Oxy, получим два уравнения движения

, ,

(2.5)

При прямолинейном движении точки, если вдоль ее траектории направить координатную ось Ох, движение будет определяться одним уравнением

,

(2.6)

Это и есть закон прямолинейного движения.

Скорость и ускорение точки при координатном способе задания движения

Пусть заданы уравнения движения точки: .

Обозначим орты осей координат . Проведем из начала координат О в движущуюся точку М радиус-вектор 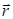. Согласно рис. 2.5 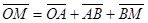или .

Скорость точки равна производной от радиус-вектора по времени. Найдем эту производную, учитывая, что орты 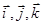имеют неизменные модули и направления, т.е. постоянны и могут быть вынесены за знак производной:

.

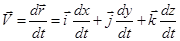Построив прямоугольный параллелепипед, ребра которого параллельны осям координат, а диагональ совпадает со скорость , получим проекции скорости на оси координат , равные алгебраическим величинам отрезков Ма, Мb, Mc.

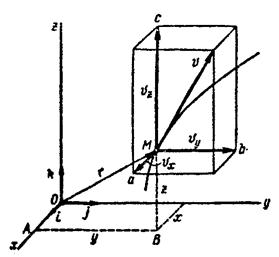Рисунок 2.5

Тогда разложение скорости на компоненты по осям координат примет вид

.

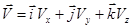Сопоставляя обе формулы, определяющие скорость находим

.

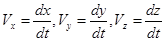(2.14)

Следовательно, проекции скорости точки на координатные оси равны первым производным от соответствующих координат точки по времени.

Пользуясь принятым обозначением производных по времени, имеем

.

(2.15)

Зная проекции скорости, можно найти её модуль и направление (т.е. углы , которые вектор образует с координатными осями) по формулам

, .

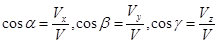(2.16)

Дата добавления: 2014-11-25