Дисконтирование по простым процентам

Для коммерческих расчетов иногда требуется определить срок ссуды и процентную ставку.

Определение срока ссуды и величины процентной ставки по простых процентам

Срок ссуды определяется по формулам:

в годах: n = (S - p) / (p*i) в днях: d = (S - p) / (p*i) * K

Величина процентной ставки определяется по формулам:

в годах: i = (S - p) / (p*n) в днях: i = (S - p) / (p*d) * K

ПРИМЕР. На какой срок выдан кредит в 300 млн.руб. под процентную ставку 60% годовых, если банк получил сумму от кредитора 380 млн.руб. Методика расчета банковская.

р = 300 млн.руб. S = 380 млн.руб. i = 0,60 К = 360 дней	d = (S - p) / (p*i) * K   d = (380 – 300) / (300*0,60) * 360 = 160 дн.
d –?

ПРИМЕР. Клиент вносит в банк денежную сумму 8 млн.руб. на 3 месяца с таким расчетом, чтобы наращенная сумма была не менее 10 млн.руб. Какой должна быть процентная ставка?

р = 8 млн.руб. S = 10 млн.руб. d / К = 1 / 4	i = (S - p) / (p*d) * K i = (10 – 8) / 8 * 4 = 1,0 Годовая процентная ставка должна быть не менее 100%
i -?

В финансовой практике часто сталкиваются с задачей, обратной наращению процентов: по заданной сумме S, которую следует уплатить через некоторое время n, необходимо определить сумму полученной ссуды Р.

Такая ситуация может возникнуть, например, при разработке условий контракта. Расчет Р по S необходим и тогда, когда проценты с суммы S удерживаются вперед, т.е. непосредственно при выдаче кредита, ссуды. В этих случаях говорят, что сумма S дисконтируется или учитывается, а сам процесс начисления процентов и их удержание называют дисконтированием или учетом, а удержанные проценты — дисконтом (discount) или сидкой.

Термин " дисконтирование " употребляется и в более широ­ком смысле – как средство определения любой стоимостной величины, относящейся к будущему, на более ранний момент времени. Такой прием часто называют приведением стоимостного показателя к некоторому, обычно начальному, моменту вре­мени.

Величину Р, найденную с помощью дисконтирования, называют современной стоимостью, или современной величиной (pre­sent value), будущего платежа S, а иногда — текущей, или капи­тализированной, стоимостью. Современная величина суммы де­нег является одним из важнейших понятий в количественном анализе финансовых операций. В большинстве случаев именно с помощью дисконтирования, а не наращения, удобно учитывать такой фактор, как время.

8 Методы дисконтирования по простым процентным ставкам

В зависимости от вида процентной ставки применяют два метода дисконтирования - математическое дисконтирование и банковский (коммерческий) учет. В первом случае применяется ставка наращения, во втором - учетная ставка.

Математическое дискон­тирование представляет собой решение задачи, обратной нара­щению первоначальной суммы ссуды. Задача, в этом случае формулируется так: какую первоначальную сумму ссуды надо выдать в долг, чтобы получить в конце срока сумму S, при ус­ловии, что на долг начисляются проценты по ставке i? При этом Р равно

_.

Установленная таким путем величина Р является современ­ной величиной суммы S, которая будет выплачена спустя п лет. Дробь 1/(1 + ni) называют дисконтным, или дисконтирующим, множителем. Этот множитель показывает, какую долю состав­ляет первоначальная величина долга в окончательной его сумме.

ПРИМЕР. Через 180 дней после подписания договора долж­ник уплатит 310 тыс. руб. Кредит выдан под 16% годовых. Какова первоначальная сумма долга при условии, что временная база равна 365 дням? Согласно (8) находим Р = 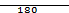= 287328,59 р.

Разность S - Р можно рассматривать не только как процен­ты, начисленные на Р, но и как дисконт с суммы S.

Суть банковского учета (учета векселей) заключается в следующем. Банк или другое финансовое учреждение до на­ступления срока платежа по векселю или ино­му платежному обязательству приобретает его у владельца по цене, которая меньше суммы, указанной на векселе, т.е. поку­пает (учитывает) его с дисконтом. Получив при наступлении срока векселя деньги, банк реализует процентный доход в виде дисконта. В свою очередь владелец векселя с помощью его уче­та имеет возможность получить деньги хотя и не в полном объ­еме, однако, ранее указанного на нем срока.

При учете векселя применяется банковский, или коммерче­ский, учет. Согласно этому методу проценты за пользование ссудой в виде дисконта начисляются на сумму, подлежащую уп­лате в конце срока. При этом применяется учет­ная ставка d.

Размер дисконта, или суммы учета равен S∙n∙d; ес­ли d - годовая учетная ставка, то n измеряется в годах. Таким образом,

Р = S - S∙n∙d = S∙(1 - n∙d),

где n- срок от момента учета до даты погашения векселя.

Дисконтный множитель здесь равен (1 - n∙d). Из формулы вытекает, что при n >1/d величина дисконтного множи­теля и, следовательно, суммы Р станет отрицательной. Иначе говоря, при относительно большом сроке векселя учет может привести к нулевой или даже отрицательной сумме Р, что ли­шено смысла. Например, при d- 20% уже пятилетний срок до­статочен для того, чтобы владелец векселя ничего не получил при его учете.

Учет посредством учетной ставки чаще всего осуществляет­ся при временной базе К = 360 дней, число дней ссуды обычно берется точным.

ПРИМЕР 7. Тратта (переводной вексель) выдан на сумму 1 млн. руб. с уплатой 17.11.2000. Владелец векселя учел его в банке 23.09.2000 по учетной ставке 20% (АСТ/360). Оставшийся до конца срока период равен 55 дням. Полученная при учете сум­ма (без уплаты комиссионных) равна

Р = 1000000(1 – 55 / 360 * 0,2) = 969444,4 руб.

Дисконт составит 30555,6 руб.

Дата добавления: 2014-11-25