Начисление сложных годовых процентов

ТЕМА 3. ТЕОРИЯ СЛОЖНЫХ ПРОЦЕНТОВ

В средне- и долгосрочных финансово-кредитных операциях, если проценты не выплачиваются сразу после их начисления, а присоединяются к сумме долга, приме­няют сложные проценты (compound interest). База для начисления сложных процентов в отличие от простых не остается постоян­ной - она увеличивается с каждым шагом во времени. Абсо­лютная сумма начисляемых процентов возрастает, и процесс увеличения суммы долга происходит с ускорением. Наращение по сложным процентам можно представить как последователь­ное реинвестирование средств, вложенных под простые про­центы на один период начисления. Присоедине­ние начисленных процентов к сумме, которая послужила базой для их начисления, часто называют капитализацией процентов.

Найдем формулу для расчета наращенной суммы при усло­вии, что проценты начисляются и капитализируются один раз в году (годовые проценты). Для этого применяется сложная став­ка наращения. При этом:

р - первоначальный размер долга (ссуды, кредита, капита­ла и т.д.),

S - наращенная сумма на конец срока ссуды,

n - срок, число лет наращения,

j - уровень годовой ставки процентов, представленный де­сятичной дробью.

Очевидно, что в конце первого года проценты равны вели­чине р∙j, а наращенная сумма составит р + р∙j = р∙(1 + j). К кон­цу второго года она достигнет величины р∙(1 + j)+ р∙(1 + j) = р∙(1 + j)² и т.д. В конце n-го года наращенная сумма будет равна

S = р∙(1 + j)ⁿ

Проценты за этот же срок в целом таковы: I = S – р.

Величину (1 + j)ⁿ называют множителем или коэффициентом наращения по сложным процентам. Значения этого множителя для целых чисел п приводятся в таблицах сложных процентов. Точность расчета множителя в практических расчетах определяется допустимой степенью округления наращенной суммы. Время при наращении по сложной ставке обычно измеряет­ся как ACT/ ACT.

ПРИМЕР. Какой величины достигнет долг, равный 1 млн. руб., через 5 лет при росте по сложной ставке 15,5% годовых? По формуле (14) находим S = 1 000 000(1 + 0,155)⁵ = 2 055 464,22 р.

Как видно, величина множителя наращения зависит от двух параметров – j и n. Следует отметить, что при большом сроке наращения даже небольшое изменение ставки заметно влияет на величину множителя. Очевидно, что очень высокая (инфляционная) процентная ставка может быть применена только для короткого срока. В противном случае результат наращения окажется бессмыслен­ным. Например, уже при j = 120% онная став­ка не столь уж давно наблюдалась в России, правда для кратко­срочных ссуд) и п = 10 имеется множи­тель наращения (1 + 1,2)¹⁰ = 2656.

Формула наращения по сложным процентам получена для годовой процентной ставки и срока, измеряемого в годах. Однако ее можно применять и при других периодах начисле­ния. В этих случаях j означает ставку за один период начисле­ния (месяц, квартал и т.д.), а n - число таких периодов. На­пример, если j - ставка за полугодие, то n - число полугодий и т.д.

2 Переменные ставки при начислении сложных процентов

Формула S = р∙(1 + j)ⁿ предполагает постоянную ставку на протяжении всего срока начисления процентов. Не­устойчивость кредитно-денежного рынка заставляет модерни­зировать "классическую" схему, например, с помощью приме­нения плавающих ставок. Естественно, что расчет на перспективу по таким ставкам весьма условен. Иное дело - расчет постфактум. В этом случае, а также тогда, когда измене­ния размеров ставок фиксируются в контракте, общий множи­тель наращения определяется как произведение частных, т.е.

S = р∙(1 + j₁)ⁿ₁ ∙ (1 + j₂)ⁿ₂ ∙…∙ (1 + j_к)ⁿ_к

где j_1, j_2, j_к - последовательные значения ставок;

п₁, п₂,..., п_к - периоды, в течение которых используются соответствующие ставки.

При этом К_н= (1 + j₁)ⁿ₁ ∙ (1 + j₂)ⁿ₂ ∙…∙ (1 + j_к)ⁿ_к

ПРИМЕР. Срок ссуды - 5 лет, договорная базовая процент­ная ставка - 12% годовых плюс маржа 0,5% в первые два года и 0,75% в оставшиеся годы. Множитель наращения в этом случае составит К_н = (1 + 0,125)²(1 + 0,1275)³ = 1,81407.

3 Начисление процентов при дробном числе лет в сложных процентах

Часто срок в го­дах для начисления процентов не является целым числом. В правилах ряда коммерческих банков для некоторых операций проценты начисляются только за целое число лет или других периодов начисления. Дробная часть периода отбрасывается. В большинстве же случаев учитывается полный срок. При этом применяют два метода. Согласно первому общему, расчет ведется непосредственно по формуле S = р∙(1 + j)ⁿ.

Второй, сме­шанный, метод предполагает начисление процентов за целое число лет по формуле сложных процентов и за дробную часть срока по формуле простых процентов:

S = р∙(1 + j)^а ∙(1 +b∙ j)

где п = а + b, a - целое число лет, b - дробная часть года.

Аналогичный метод применяется и в случаях, когда перио­дом начисления является полугодие, квартал или месяц.

При выборе метода расчета следует иметь в виду, что мно­житель наращения по смешанному методу оказывается не­сколько больше, чем по общему, так как для n < 1 справедли­во соотношение 1 + nj > (1 + j) в n степени. Наибольшая разница наблю­дается при b = 1/2.

ПРИМЕР 4. Кредит в размере 3 млн. р. выдан на 2 года и 160 дней (n = 3,43836 года) под 16,5% сложных годовых. Сумму долга на конец срока: S = 3 000 000 х 1,165³,⁴³⁸³⁶ = 5 071 935,98 руб., в свою очередь, смешанный метод дает S = 3 000 000 х 1.165³ х (1 + 0,43836 х 0,165) = 5 086 595,98 р.

4 Наращение процентов при расчете сложных процентов т раз в году с использованием номинальной процентной ставки

В современных условиях проценты капи­тализируются, как правило, не один, а несколько раз в году - по полугодиям, кварталам и т.д. Некоторые зарубежные коммерческие банки практикуют даже ежедневное начисление процентов. При начислении процентов несколько раз в году можно восполь­зоваться формулой S = р∙(1 + j)ⁿ. Параметр m в этих условиях будет озна­чать число периодов начисления, а под ставкой j следует пони­мать ставку за соответствующий период. Например, при поквар­тальном начислении процентов за 5 лет общее число периодов начисления составит 5 х 4 = 20. Множитель наращения по квар­тальной (сложной) ставке 8% равен в этом случае 1,08²⁰ = 4,6609. На практике, как правило, в контрактах обычно фиксируется не ставка за период начисления, а годовая ставка, одновременно указывается период начисления процентов.

Итак, пусть годовая ставка равна j, число периодов начисле­ния в году - m. Каждый раз проценты начисляются по ставке j/m. Ставку j называют номинальной (nominal rate). Формулу на­ращения теперь можно представить следующим образом:

К_н = (1 + j/m)^n*m

При этом S = р∙(1 + j/m)^n*m.

Если N целое число (N = n∙m), то в большинстве случаев для определения величины множителя наращения можно восполь­зоваться таблицей сложных процентов..

Нетрудно догадаться, что чем чаще начисляются проценты, тем быстрее идет процесс наращения (цепной процесс).

5 Наращение процентов при расчете сложных процентов т раз в году с использованием эффективной процентной ставки

Эффективная ставка измеряет тот реальный относительный доход, который получают в целом за год. Иначе говоря, эффективная ставка - это годовая ставка сложных процентов, которая дает тот же ре­зультат, что и m-разовое начисление процентов по ставке j/m.

Обозначим эффективную ставку через i. По определению мно­жители наращения по двум ставкам (эффективной и номиналь­ной при m-разовом начислении) должны быть равны друг другу:

(1 + i)ⁿ = (1 + j/m)^n∙m (18)

Из равенства множителей наращения следует

i_эф =(1 + j/m) ^m – 1 (19)

Эффективная ставка при т > 1 больше номинальной.

Замена в договоре номинальной ставки j при m-разовом на­числении процентов на эффективную ставку i не изменяет фи­нансовых обязательств участвующих сторон. Обе ставки эквивалентны в финансовом отношении. Отсюда, кстати, следует, что разные по величине номинальные ставки оказываются эквива­лентными, если соответствующие им эффективные ставки име­ют одну величину.

ПРИМЕР. Каков размер эффективной ставки, если номиналь­ная ставка равна 25% при помесячном начислении процентов? Имеем i_эф =(1 + 0,25/12) ¹² – 1 = 0,281

6 Операции со сложной учетной ставкой – учет по сложной ставке

В практике учетных опера­ций иногда применяют сложную учетную ставку. В этих случаях процесс дисконтирования происхо­дит с замедлением, так как каждый раз учетная ставка приме­няется не к первоначальной сумме (как при простой учетной ставке), а к сумме, дисконтированной на предыдущем шаге во времени. Дисконтирование по сложной учетной ставке осуще­ствляется по, формуле

,

где d – сложная годовая учетная ставка.

ПРИМЕР. Долговое обязательство на сумму 5 млн. руб., срок оплаты которого наступает через 5 лет, продано с дисконтом по сложной учетной ставке 15 % годовых. Найти размер суммы, полученной за долг, и величину дисконта (в стоимостном выражении).

Решение

тыс. р.,

тыс. р.

Если применить простую учетную ставку того же размера, то:

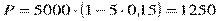тыс. р.,

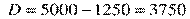тыс. руб.

Т. о., дисконтирование по сложной учетной ставке для должника выгоднее, чем дисконтирование по простой учетной ставке, т. к.

– дисконтный множитель для простой учетной ставки,

– дисконтный множитель для сложной учетной ставки,

где d_s, d – простая и сложная учетные ставки.

Согласно первой формуле значение дисконтирующего множителя равномерно уменьшается по мере роста n и достигает нуля при . Согласно второй формуле множитель экспоненциально уменьшается и достигает нуля лишь в пределе при .

7 Операции со сложной учетной ставкой – номинальная и эффективная учетные ставки, наращение по сложной учетной ставке

Дисконтирование может производиться не один раз в году, а m раз в год, т. е. каждый раз учет производится по ставке 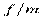. В этом случае

,

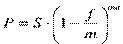где f – номинальная годовая учетная ставка.

Эффективная учетная ставка d показывает степень дисконтирования за год. Ее определяют из равенства дисконтных множителей:

Откуда .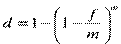

В свою очередь . Эффективная учетная ставка меньше номинальной при m > 1.

ПРИМЕР. Представлено долговое обязательство на сумму 5 млн. руб., срок оплаты которого наступает через 5 лет. Найти сумму, полученную при поквартальном учете по номинальной учетной ставке 15 %, и эффективную учетную ставку.

Имеем f = 0,15; m = 4; n = 5; m ∙ n = 20. 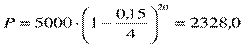тыс. руб.

Эффективная учетная ставка составит , или 14,177 %.

Иногда наращенную сумму получают и с помощью сложной учетной ставки.

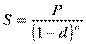Из формул и следует: и .

Множитель наращения при использовании сложной учетной ставки d равен , где d — сложная годовая учетная ставка.

Дата добавления: 2014-11-25