Методы измерения тесноты связи

Измерение тесноты связи при помощи дисперсионно­го и корреляционного анализа связано с определенными сложностями и требует громоздких вычислений. Для ори­ентировочной оценки тесноты связи пользуются прибли­женными показателями, не требующими сложных, тру­доемких расчетов. К ним относятся: коэффициент кор­реляции знаков Фехнера, коэффициент корреляции ран­гов, коэффициент ассоциации и коэффициент взаимной сопряженности.

Коэффициент корреляции знаков основан на сопоставлении знаков отклонений от средней и подсчете числа случаев совпадения и несовпадения знаков, а не на сопоставлении попарно размеров отклонений индивидуальных значений факторного и результативного признаков от средней (х— х) и (у — у):

(8.34)

где и — число пар с одинаковыми знаками отклонений х и у от х и у; v — число пар с разными знаками отклонений х и у от х и у. Коэффициент корреляции знаков колеблется в пределах от -1 до +1. Чем ближе коэффициент к 1, тем теснее связь. Если и > v, то i > 0, так как число согласо­ванных знаков больше, чем несогласованных, и связь пря­мая. При и < v имеем i < 0, потому что число несогласованных знаков больше, чем согласованных, и связь об­ратная. Если и = v, то I=0, и связи нет.

Коэффициент кор­реляции рангов исчисляется не по первичным данным, а по рангам (порядковым номерам), которые присваивают­ся всем значениям изучаемых признаков, расположенным и порядке их возрастания. Если значения признака совпа­дают, то определяется средний ранг путем деления сум­мы рангов на число значений. Коэффициент корреляции рангов определяется по формуле:

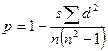(8.35)

где d² — квадрат разности рангов для каждой едини­цы, d =х — у; п — число рангов; s — средний ранг.

Коэффициент корреляции рангов также колеблется в пределах от -1 до +1. Если ранги по обоим признакам совпадают, то ηd² =0, значит, р = 1 и, следовательно, связь полная прямая. Если р = -1, связь полная обрат­ная, при р =0 связь между признаками отсутствует.

Коэффициент ассоциации применяется для установления меры связи между двумя качественными альтернативными признаками. Для его вычисления строится комбинационная четырехклеточная таблица, которая выражает связь между двумя альтерна­тивными явлениями.

Коэффициент ассоциации рассчитывается по формуле:

(8.36)

Коэффициент ассоциации также изменяется от -1 до +1. Чем А ближе к единице, тем сильнее связаны между собой изучаемые признаки. При ad> bс связь прямая, а при ad< bс связь обратная, при ad = bс A = 0 и связь отсутствует.

В тех слу­чаях, когда требуется установить связь между качествен­ными признаками, каждый из которых состоит из трех и более групп, применяется коэффициент взаимной сопря­женности.

Различия между условным и безусловным распреде­лением свидетельствуют о влиянии факторного признака на распределение совокупности по результативному при­знаку, т.е. о наличии связи между факторным и результа­тивным признаками, а чем больше эти различия, тем в большей мере признаки связаны между собой, тем теснее связь между ними.

Коэффици­ентом взаимной сопряженности определяется по сле­дующей формуле:

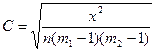(8.37)

где п — число единиц совокупности; m₁ и т₂ — число групп по первому и второму признакам; χ² — показатель абсолютной квадратической сопряженности Пирсона, ха­рактеризующий близость условных распределений к безусловным, который, как и критерий χ²исчисляется по формуле:

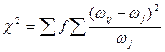(8.38)

где . — частости условного распределения в i-й строке; —частости безусловного распределения; j — номер столбца.

Если признаки независимы, то w_ij.. = ., откуда χ² = О и, значит, С = 0. Если же связь функциональная, то коэф­фициент взаимной сопряженности будет равен единице.

Тема 9. Статистическое изучение динамики социально – экономический явлений

Дата добавления: 2014-11-25