Статистические показатели динамики

Сопоставимость в рядах динамики

Основным условием для получения правильных выводов при ана­лизе рядов динамики является сопоставимость его элементов Показатели ряда динамики, подлежащие сопоставлению, должны быть однородны по экономическому содержанию. Основные условия, обеспечивающие сопоста­вимость в рядах динамики:

· единые единицы измерения (цены берутся за определенный период);

· единство территории;

· единство методологии сбора, учета и обобщения информа­ции.

Для того чтобы привести уровни ряда динамики к сопоставимому виду, иногда приходится прибегать к приему, который называется «смыка­ние рядов динамики». Под смыканием понимают объединение в один ряд (более длинный) двух или несколько рядов динамики, уровни которых ис­числены по разной методологии или территориальным границам. Для осу­ществления смыкания необходимо, чтобы для одного из периодов (переход­ного) имелись данные, исчисленные по разной методологии (или в разных границах).

При анализе рядов динамики можно решить следующие ос­новные задачи:

1.определить интенсивность изменений в уровнях ряда из периода в период или от даты к дате;

2.определить средние показатели за рассматриваемый период;

3.выявить закономерности изменения явления во времени и в целом за рассматриваемый период;

4.выявить факторы, вызывающие изменение изучаемого явления во времени;

5.прогнозировать развитие явления на будущее.

В основе расчета показателей рядов динамики лежит сравнение его уровней. В зависимости от применяемого способа сопоставления показатели динамики могут вычисляться на постоянной и переменной базах сравнения.

Для расчета показателей динамики на постоянной базе сравнения каждый уровень ряда сравнивается с одним и тем же базисным уровнем. Исчисляемые при этом показатели называются базисными. Для расчета по­казателей динамики на переменной базе каждый последующий уровень ряда сравнивается с предыдущем. вычисленные таким образом показатели дина­мики называются цепными.

· Абсолютные показатели динамики

Важнейшим статистическим показателем динами является абсолют­ный прирост, который определяется в разносном сопоставлении двух уров­ней ряда динамики в единицах измерения исходной информации.

Базисный абсолютный прирост исчисляется как разность между сравниваемым уровнем (y_i) уровнем, принятым за постоянную базу сравне­ния (начальным) (у_оi):

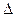y_бi = y_i - y_oi (9.1.)

Цепной абсолютный прирост – разность между сравниваемым уровнем (y_i) и уровнем, который ему предшествует (y_i-1):

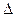y_цi = y_i –y_i-1 (9.2.)

Абсолютный прирост может иметь и отрицательный знак, показывающий на сколько уровень изучаемого периода ниже базисного.

Между базисными и цепными абсолютными приростами имеется связь: сумма цепных абсолютных приростов равна базисному абсолютному приросту последнего периода ряда динамики.

(9.3.)

· Относительные показатели динамики

Распространенным статистиче­ским показателем динамики является темп роста. Он характеризует отно­шение двух уровней ряда и может выражаться в виде коэффициента или в процентах.

Базисные темпы роста исчисляются делением сравниваемого уровня y_i на уровень, принятый за постоянную базу сравнения y_oi.

Тр_бi = y_i: y_oi (9.4.)

Цепные темпы роста исчисля­ются делением сравниваемого уровня y_i на предыдущий уровень y_{i - 1}.

Тр_цi = y_i: y_i-1 (9.5.)

Если темп роста больше еди­ницы (или 100%), то это показывает на увеличение изучаемого уровня по сравнению с базисным. Темп роста, равный единице (или 100%), показывает, что уровень изучаемого периода не изменился по сравнению с базисным. Темп роста меньше единицы (или 100%) показывает на уменьшение уровня изучаемого периода по сравнению с базисным. Темп роста всегда имеет по­ложительный знак.

Произведение последовательных цепных темпов роста равно базисному темпу роста, а частное от деления последующего базисного темпа роста на предыдущий равно соответствую­щему цепному темпу роста.

Темпы прироста характеризуют абсолютный прирост в относительных величинах. Исчисленный в процентах темп прироста показывает, на сколько процентов изменился сравниваемый уровень с уровнем, принятым за базу сравнения.

Базисный темп прироста вычисля­ется делением сравниваемого базисного абсолютного прироста у_бi на уровень, принятый за постоянную базу сравнения y_оi.

Тп_{бi =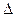} у_бi: y_оi (9.6.)

Цепной темп прироста – это от­ношение сравниваемого цепного абсолютного прироста у_цi к предыдущему уровню y_i-1.

Тп_цi = 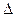y _цi: y_i-1 (9.7.)

Взаимосвязь темпа роста и темпа прироста:

Тп_i (%) = Тр_i (%) – 100 (в процентах) (9.8.)

Тп_i = Тр_i –1 (в коэффициентах) (9.9.)

Темп наращивания характери­зует наращивание во времени экономического потенциала и определяется как отношение цепного абсолютного прироста у_цi к начальному уровню у_оi, выражается в процентах. Может быть как положительным, так и отрица­тельным.

Тн_i = у_цi: у_оi (9.10.)

· Средние показатели динамики

Средний уровень ряда динамики характеризует типическую вели­чину абсолютных уровней ряда.

В интервальных рядах динамики средний уровень определяется де­лением суммы уровней на их число.

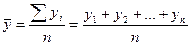(9.11.)

у_1, у_2, у_n - уровни ряда;

n - число рядов.

В моментном ряду динамики с равностоящими датами времени средний уровень определяется по формуле:

(9.12.)

В моментном ряду динамики с неравностоящими датами средний уровень определяется по формуле:

(9.13.)

y_i – уровни ряда динамики, сохранившиеся без изменения в течение промежутка времени t_i.

Средний абсолютный прирост представляет собой обобщенную ха­рактеристику индивидуальных абсолютных приростов ряда динамики и оп­ределяется как частное от деления суммы цепных абсолютных приростов на их число.

(9.14)

Средний темп роста – обобщающая характеристика индивидуаль­ных темпов роста ряда динамики.

(9.15.)

Tp₁, Тр_{2, …}, Тр_n- индивидуальные (цепные) темпы роста (в ко­эффициентах);

n - число индивидуальных темпов роста.

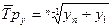(9.16.)

Средний темп прироста можно определить на основе взаимосвязи между темпами роста и прироста.

(9.17.)

Дата добавления: 2014-11-25