Оценка факторов

Значение каждого критериального фактора следует оценить с точки зрения привлекательности отрасли по 5 балльной шкале:

3 балла – фактор отражает средний уровень привлекательности отрасли;

4 балла — уровень «выше среднего»;

5 баллов – высокий уровень;

2 балла – уровень ниже среднего;

1 балл – низкий уровень.

Балльная оценка значений факторов выполняется относительно среднего регионального или рекомендуемого их значения. Так, если уровень рентабельности отрасли приблизительно равен среднерегиональному, то должна быть выставлена оценка 3 балла (отрасль является средней по привлекательности в регионе с точки зрения рентабельности). Если рентабельность отрасли окажется выше, оценка будет 4 или 5, так как чем выше рентабельность тем привлекательнее отрасль для бизнеса.

При оценке соотношения потенциала и прогноза спроса, стандартное значение мы приняли на уровне 3,0, оно и будет соответствовать оценке в 3 балла – средней привлекательности. При меньшем значении привлекательность отрасли по данному фактору будет оценена ниже, при большем – выше 3 баллов.

При оценке конкуренции, оценки будут обратно пропорциональны интенсивности конкурентной борьбы, поскольку отрасль тем более привлекательна, чем меньше конкуренция.

В целом оценки определяются с позиций стороннего наблюдателя, а не участника отрасли. Однако в некоторых случаях конкурентное давление не может быть оценено без учета текущего положения фирмы, проводящей анализ. Так, для отраслевого лидера, обладающего бесспорными преимуществами и вытесняющего конкурентов, конкуренция в отрасли будет оценена как незначительная (в действительности, никто из конкурентов не может ему противостоять), и оценка будет высокой (то есть отрасль будет весьма привлекательна для него). Однако для всех остальных конкурентов отрасль будет представляться высоко конкурентной, и оценка привлекательности окажется низкой. Для учета положения нашего бизнеса (отделения), следует обратить внимание на данные таблицы 2 задания, где приводятся доли фирмы и крупнейшего ее конкурента на рынке.

Оцененные факторы не являются равнозначными, некоторые из них более важны, в большей степени характеризуют привлекательность отрасли. Для учета различия в степени значимости (важности) факторов необходимо определить их весовые коэффициенты (веса). В данном проекте рекомендуется применить метод анализа иерархий (МАИ), разработанный Т. Саати. [9],[10].

Первым этапом применения МАИ является структурирование проблемы в виде иерархии. В данном курсовом проекте проблему характеризует простейшая двухуровневая иерархия. В ее вершине будет показатель «привлекательность отрасли». Второй уровень образуют отобранные ранее факторы привлекательности отрасли.

На втором этапе элементы иерархии сравниваются экспертом попарно по отношению к их воздействию на общую для них характеристику. В нашем случае попарно будут сравниваться выбранные факторы привлекательности, с точки зрения того, насколько они отражают «привлекательность отрасли».

Система парных сравнений снижает требования к экспертам, оценивающим проблему, упрощает их работу, так как значительно проще сравнивать по два показателя (определяя, какой из них более важен), чем оценивать все показатели совместно.

Результат парных сравнений эксперт оформляет в виде квадратной матрицы. Элементом матрицы а(i, j) является относительная важность фактора i (т.е. фактора в строке) относительно фактора j (в столбце), оцениваемая по шкале от 1 до 9, где балльные оценки имеют следующий смысл:

1 — равная важность факторов в строке и столбце;

3 — умеренное превосходство важности фактора в строке над фактором в столбце;

5 — существенное или сильное превосходство;

7 — значительное превосходство;

9 — очень сильное превосходство;

2, 4, 6, 8 — промежуточные значения.

Если же, напротив, фактор j оказался более важным по сравнению с фактором i, значения будут обратными – от 1/2 до 1/9.

Матрица обладает следующими свойствами:

1. Ее диагональ образуют единицы, поскольку при сравнении факторов самих с собой они равноважны;

2. Для любых i, j а(i, j) = 1/ а(j, i). Понятно, что если фактор i с какой-либо интенсивностью важнее j, то с такой же интенсивностью фактор j будет менее важен, чем i. Пользуясь этим свойством, достаточно заполнить лишь половину матрицы, выше или ниже диагонали, а другую половину заполнить обратными значениями.

После заполнения матрицы, необходимо перейти от парных оценок к оценкам важности и весам факторов. В общем случае задача сводится к нахождению собственного вектора матрицы, однако, учитывая высокую ее трудоемкость, часто пользуются приблизительными вычислениями, используя среднюю геометрическую парных оценок по строкам матрицы:

,

где X_i – оценка важности фактора i (вес фактора, не приведенный к единице);

а_ij – оценка относительной важности фактора i по отношению к j;

n–количество оцениваемых факторов (размерность матрицы).

Веса затем должны быть нормализованы, то есть, приведены к единице:

,

где P_i –нормализованный вес фактора, Σ P_i = 1.

В процессе оценки эксперт может допустить ошибку. Например, он может предпочесть фактор 1 фактору 2, фактор 2 фактору 3, и одновременно оценить фактор 1 как менее важный по сравнению с третьим. Для выявления подобных ошибок следует рассчитать индекс согласованности (ИС) и отношение согласованности матрицы парных сравнений (ОС):

, , ,

где СС- средняя случайная согласованность матрицы, которая получилась бы при случайном выборе количественных суждений из нашей шкалы, и образовании обратно симметричной матрицы.

Средняя случайная согласованность зависит от размерности матрицы и выбирается из таблицы 6.

Таблица 6

Значения средней случайной согласованности

Размерность матрицы (n)
Случайная согласованность			0.58	0.9	1.12	1.24	1.32	1.41	1.45	1.49

Величина ОС должна быть менее 0,1 (10%). В случае больших величин эксперту необходимо проверить свои суждения.

Пример (по таблице 7). Пусть выбраны факторы: «потенциал спроса», «уровень конкуренции» и «рентабельность». Предположим, отрасль находится на стадии зрелости (в развернутой фазе), тогда наиболее важным фактором будет рентабельность, затем уровень конкуренции и потенциал спроса. Записываем факторы в матрице в порядке убывания значимости, тогда при ее заполнении оценки выше диагонали будут больше единицы. Заносим единицы в диагогальные ячейки матрицы.

Фактор рентабельности умеренно важнее уровня конкуренции, ведь острая конкуренция может привести к падению рентабельности в будущем – оценка 3 в ячейку а_12. По сравнению с потенциалом спроса, рентабельность в значительно большей степени отражает привлекательность отрасли, поскольку на стадии зрелости главная задача – получение максимальной прибыли. Оценка 5 заносится в ячейку а₁₃. Факторы конкуренции и потенциала спроса по значимости близки, превосходство первого фактора несущественное. Оценка может быть 2 балла.

Далее заполняем оставшиеся ячейки обратными значениями, проводим вычисления.

Таблица 7

Матрица попарного сравнения (пример)

Факторы	1.Рентабельность	2.Уровень конкуренции	3.Потенциал спроса	Средняя геометрическая оценка важности Xi	Нормализованные веса Pi
1.Рентабельность					2,466/ 3,804= 0,648
2.Уровень конкуренции	1/3		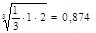		0,874/ 3,804= 0,23
3.Потенци-ал спроса	1/5	1/2			0,46/ 3,8= 0,122
	1.533	4.5		3,804	1,00

λmax = 1,533*0,648+4,5*0,23+8*0,122=3,005,

ИС=(3,005-3)/2=0,0025. ОС=0,0025/0,58=0,004<0,1.

Индекс согласованности в пределах нормы.

Обоснование оценок самих факторов, и расчет комплексной оценки оформляется по примеру таблицы 8.

Таблица 8

Расчет оценки привлекательности отрасли (пример)

Фактор	Значение	Оценка	Вес	Комплексная оценка
1. Рентабельность	38%, намного выше среднерегиональной (25%)		0,648	5^0,648*3^0,23*4^0,122=4,326 Высокое значение привлекательности отрасли
2. Уровень конкуренции	Средний. Неценовая конкуренция при отсутствии явного лидера (ИХ близок к минимальному), на одородном рынке (6 конкурентов на 2 сегментах), при отсутствии агрессивной борьбы.		0,23
3.Потен-циал спроса	Соотношение потенциала и прогноза спроса 6,5.		0,122

При вычислении комплексной оценки (КО) предпочтение отдается средней геометрической, вычисляемой по формуле:

,

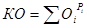где О_i – оценка фактора i;

P_i – вес фактора i.

При использовании средней арифметической может произойти взаимная компенсация значений оценок факторов, приводящая к парадоксальным выводам. Для выбранных факторов, высокое значение одного не может компенсировать слишком низкое значение другого. Так, высокая рентабельность не повысит привлекательность, если потенциал спроса исчерпан и рынок близок к сокращению. Предположим, оценка одного из факторов оказывается равной нулю. Тогда средняя геометрическая также обращается в ноль при любых значениях прочих оценок, что логично отражает крайне низкую привлекательность отрасли. Но если использовать среднюю арифметическую, при высоких значениях остальных оценок, средняя может оказаться и выше трех баллов, формируя ошибочный вывод.

Дата добавления: 2014-11-25