Методики сравнения средних двух статистических выборок, полученных при исследовании оперативно-тактических действий

Билет 2

Поставить две серии опытов в одинаковых условиях (по n опытов в каждой серии). Результаты первой серии опытов заносить во второй столбец табл.8.7, второй серии в четвертый столбец.

Таблица 8.7

§ По формуле (8.40) найти значение выборочных средних ₁ и ₂

для каждой из выборок:

(8.40)

Где п - число опытов;

y_i - результат i -го опыта.

§ По формуле (8.41) найти оценки дисперсий S₁² и S₂² для каждой из выборок:

(8.41)

§ Проверить гипотезу об однородности двух выборочных сред них ₁ и ₂. Для этого:

а) по формуле (8.43) найти среднюю оценку дисперсии

(8.43)

б) по формуле (8.44) найти значение t_расч:

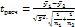(8.44)

в) сравнить найденное значение t_расч с полученным значением t_табл;

г) если t_расч≤t_табл принять гипотезу об однородности выборочных средних ₁ и ₂, В противном случае нулевую гипотезу следует отвергнуть.

§ Проанализировать полученные результаты. Сделать выводы: для средних значений обеих серий опытов справедлива /несправедлива нулевая гипотеза. Между ними нет существенного различия /имеется существенное различие.

2. Матрица полного факторного плана 2² и его геометрическое толкование в натуральных и нормализированных обозначениях. Расчет коэффициентов уравнения регрессии ПФП – 2².

Полным факторным планам можно дать геометрическое толкование. Для плана с двумя факторами рассмотрим факторную плоскость, то есть координатную плоскость, по оси абсцисс которой откладываются значения факторах х₁, а по оси ординат - значение фактора х₂ (см. рис.11.1). Построим на этой плоскости точки, координаты которых соответствуют нормализованным значениям факторов в опытах 1-4 ПФП 2² (табл.11.3). Точки этого плана образуют вершины квадрата, центр которого совпадает с началом координат. Внутренность квадрата является областью варьирования нормализованных факторов.

На факторной плоскости (рис.11.2) изображены точки этого же плана в натуральных обозначениях факторов. В этих координатах область варьирования факторов представляет собой внутренность прямоугольника.

Рис.11.1 Геометрическое толкование полных факторных планов 2². а) нормализированные факторы, б) натуральные факторы

Линейная модель в этом случае имеет вид

ŷ = b₀+b₁x₁+b₂x₂. (11.11)

Коэффициенты регрессии вычисляются по формулам:

(11.12)

(11.13)

(11.14)

Дата добавления: 2014-11-25