Билет 6

Роль коэффициента Стьюдента в изучении параметров оперативно тактических действий пожарных подразделений. Привести примеры.

Проверять нулевую гипотезу относительно средних ₁ и ₂ двухвыборок можно, только если соответствующие оценки дисперсий S₁² и S₂² однородны. Поэтому проверке нулевой гипотезы относительно средних должна предшествовать проверка однородности оценок дисперсий этих выборок.

Проверка нулевой гипотезы относительно двух выборочных средних ₁ и ₂ производится следующим образом.

После проверки однородности оценок дисперсий S₁² и S₂² находят:

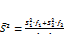(8.28)

и суммарное число степеней свободы

f = f₁ + f₂, (8.29)

где f ₁ и f ₂ - число степеней свободы первой и второй выборок соответственно.

Далее рассчитывают значение величины t _расч:

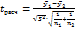(8.30)

По табл. п 2 Приложения для данного числа степеней свободы f и уровня значимости q находят значение t_табл. Величина t _табл показывает, какое наибольшее значение может принять величина t_расч при условии, что нулевая гипотеза о равенстве двух выборочных средних справедлива. Следовательно, если t _pасч< t _табл, принимают гипотезу о том, что ₁ и ₂ являются оценками одного и того же генерального среднего (математического ожидания) М_у, то есть расхождение между ₁ и ₂ несущественно (незначимо).

Изложенная процедура проверки нулевой гипотезы о двух выборочных средних называется проверкой по t - критерию Стьюдента.

1. Методика построения матрицы дробного многофакторного эксперимента без дублирования опытов для исследования оперативно – тактических действий пожарных подразделений.

Дробные факторные планы (ДФП), как и полные факторные планы (ПФП), предназначены для построения математической модели объекта. При заданном числе факторов ДФП содержат меньшее число опытов по сравнению с ПФП. Но эта экономия достигается ценой упрощения математической модели.

Напомним, что по результатам ПФП 2^k можно оценить свободный член в математической модели, все линейные коэффициенты регрессии и все взаимодействия факторов. Однако во многих случаях учёт всех взаимодействий факторов не вызывается необходимостью. Так, при первоначальном изучении объектов широко применяются эксперименты с целью получения линейной модели. Для k варьируемых факторов такая модель имеет следующий вид: (12.1) и содержит (k + 1) коэффициент регрессии

(12.1)

Эксперимент, позволяющий отыскать эти коэффициенты, должен содержать не менее чем (k + 1) опытов. С точки зрения экономии средств, желательно, чтобы число опытов N не слишком превышало эту величину. С этой позиции ПФП при отыскании линейной модели неудовлетворительны. В силу соотношения N = 2^k число опытов ПФП существенно превосходит величину (k + 1), начиная уже с трёх факторов. Полные факторные планы неэкономичны, даже если экспериментатора интересуют помимо линейных коэффициентов регрессии некоторые (но не все) взаимодействия факторов.

Пусть, например, по результатам эксперимента с шестью факторами (k = 6) необходимо оценить свободный член, линейные коэффициенты регрессии и парные взаимодействия. Минимально необходимое для этого число опытов равно числу коэффициентов регрессии:

(12.2)

в то время как ПФП 2^k шести факторов содержит N = 2⁶ = 64 опыта.

Дробные факторные планы позволяют сократить число опытов по сравнению с ПФП в случае, если в уравнении регрессии можно заранее пренебречь некоторыми взаимодействиями факторов. Для уяснения идеи построения дробных факторных планов обратимся сначала к плану ПФП 2² с двумя факторами (табл. 12.1).

Таблица12.1

Матрица базисных функций ПФП 2² для модели (12.2)

Собственно экспериментальным планом являются только столбцы 3 и 4 табл. 12.1. Столбец х₀ добавлен для вычисления коэффициента регрессии b₀, а столбец x₁х₂ - для вычисления коэффициента b₁₂ при произведении факторов x₁ и х₂. Следует отметить, что полученная матрица базисных функций удовлетворяет трём свойствам - (11.5) - (11.7). По результатам такого эксперимента можно получить модель в виде

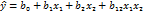(12.3)

Предположим теперь, что имеется объект с тремя варьируемыми факторами x₁, х₂, х₃, причём целью эксперимента является построение линейной модели, то есть имеются основания пренебречь всеми взаимодействиями факторов. В таком случае можно опять воспользоваться матрицей плана 2² в табл. 12.1. Потребуем, чтобы в этом эксперименте факторы x₁ и х₂ по-прежнему варьировались в соответствии с элементами столбцов 3 и 4, а фактор х₃ варьировался так же как и взаимодействие факторов x₁ х₂ (столбец 5 табл. 12.1.).

Таким образом, для эксперимента с тремя факторами получен план из четырёх опытов, по результатам которого можно построить линейную модель:

(12.4)

Перепишем матрицу этого плана в табл. 12.2

Таблица12.2

Планы такого типа называются дробными факторными планами (ДФП) или дробными репликами полных факторных планов. В частности, план, приведённый в табл. 12.2, называется полурепликой (или 1/2 реплики) от ПФП 2². Его обозначение 2^3-1. Здесь 3 - число факторов, а единица вверху символизирует тот факт, что только одно взаимодействие заменяется новым фактором. Именно такие ДФП и называются полурепликами.

В ДФП 2^3-1фактор х₃ варьируется одинаково с парным взаимодействием x₁ х₂. Поэтому в уравнении регрессии нельзя отделить влияние фактора х₃ от влияния взаимодействия x₁ х₂. Если обозначить через β истинные величины соответствующих коэффициентов регрессии, то можно сказать, что коэффициент β₃ даёт совместную оценку двух истинных коэффициентов регрессии β ₃ и β₁₂: b₃ → β ₃ + β₁₂ - это так называемая смешанная оценка.

Если построить столбцы х₁ х₃ и х₂ х ₃, то легко убедиться, что они совпадут со столбцами х ₂ и х ₁ соответственно (рекомендуется проделать это самостоятельно). Следовательно, имеем дополнительно смешанные оценки:

(12.5)

(12.6)

При построении данной полуреплики2^3-1было использовано соотношение х₃ = х₁ х₂, которое называется генератором плана. Умножим обе его части на х₃: х₃₂= х₁ х₂ х₃. Но = 1, так как нормализованный фактор х₃ в эксперименте равен либо +1, либо -1; следовательно, имеем 1 = х₁х₂ х ₃.

Такое соотношение, в левой части которого стоит 1, а в правой - некоторое произведение факторов, называется определяющим контрастом (ОК) данной реплики. С помощью ОК легко определить систему смешивания оценок, не прибегая к построению дополнительных столбцов. Для этого обе части ОК умножаются поочерёдно на х₁ х₂ х₃. Получим х₁= х₂ х₃. Откуда следует:

(12.7)

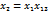(12.8)

откуда ;

Отметим, что, приравняв х₃ = - х₁ х₂, можно было получить другую полуреплику2^3-1. А обе эти полуреплики, взятые вместе, составят ПФП 2³.

Формулы для расчёта коэффициентов регрессии ПФП остаются полностью справедливыми и для ДФП.

Обратимся к построению дробных факторных планов на основе ПФП 2³. Матрица базисных функций этого плана приведена в табл. 12.3.

Таблица 12.3

Матрица базисных функций ПФП 23

Имеется несколько способов построения полуреплики с четырьмя факторами на основе этого плана в зависимости от того, каким из взаимодействий решено пренебречь. Так, пренебрегая тройным взаимодействием х₁ х₂ х₃ и заменив соответствующий столбец фактором х ₄, получим следующий план для четырёх факторов (одна из полуреплик2^4-1, табл. 12.4).

Для этого плана имеем генератор х₄= х₁х₂х₃. ОК равен 1 = х₁х₂х₃= х₄. Умножая OK последовательно на х₁, х₂, х₃, х₁х₂, х₁х₃, х₂х₃, получаем новые генераторы: х₁ = х₂х₃ х₄; х₂ = х₁ х₃ х₄; х₃ = х₁ х₂ х₄; х₁ х₂ = х₃ х₄; х₁ х₃ = х₂ х₄; х₂ х₃ = х₁ х₄.

В результате имеем следующую систему смешивания оценок:

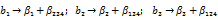
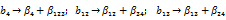
Таблица 12.4

ПФП 2^{4– 1} х₄= х₁х₂х₃

В уравнение регрессии, построенное по результатам реализации такого плана, можно включить, кроме линейных членов, все парные взаимодействия, приведённые в плане табл. 12.3:

(12.9)

Однако надо помнить о системе смешивания. К примеру, коэффициент b₁₂ оценивает не только при β ₁₂, но и β _34.

План в табл. 12.4, используемый для построения модели (12.9), является насыщенным, число опытов в нём N = 8 равно числу оцениваемых коэффициентов регрессии. Поэтому нет возможности проверить адекватность модели. Такую проверку можно сделать, если упростить уравнение (12.9), пренебрегая в нём дополнительно ещё некоторыми взаимодействиями.

Рассмотрим другой вариант полуреплики, приравняв, например, х₄ парному взаимодействию х₁ х₃. Этот план приведён в табл. 12.5.

ОК такой реплики: 1 = х ₁ х ₃ х ₄. Генераторы плана: х ₁ = х ₃ х ₄;

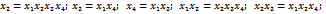
Таблица 12.5

ДФП 2^{4- 1} х₄ = х₁х₃

Система смешивания оценок:

Сравнивая системы смешивания оценок для двух последних планов, можно убедиться в преимуществах плана с OK 1 = x₁ х₂х₃ х₄. Для него оценки линейных коэффициентов регрессии смешаны лишь с тройными взаимодействиями, в то время как для плана с OK 1 = x₁ х₃ х₄ некоторые из этих оценок смешаны с парными взаимодействиями. Отсюда следует вывод: с точки зрения системы смешивания оценок, лучше выбирать реплипки, в правой части ОК которых стоит максимальное число членов.

Кроме предложенных вариантов, можно рассмотреть ещё 6 способов построения полуреплик на основе ПФП 2³. Их генераторы:

Идею построения ДФП можно развивать дальше, заменяя в планах ПФП не одно, а большее число взаимодействий новыми факторами. При замене двух взаимодействий новыми факторами получим четверть-реплики (или 1/4 реплики) ПФП. Их условное обозначение 2^{к- 2}.

В табл. 12.6 приведён план 1/4 реплики для 5 факторов, полученный заменой в ПФП 23взаимодействий x₁ х₂ х₃ и х₂ х₃ факторами х₄ и х₅ соответственно.

Таблица 12.6

ДФП 2^{5 - 2}

При замене в ПФП трёх взаимодействий новыми факторами получают 1/8 реплики ПФП, обозначаемые 2^к-3 и т. д.

На основе ПФП 2³ можно построить дробную реплику, включающую самое большее 7 варьируемых факторов. Это будет план 2^{7 - 4}, представляющий собой 1/16 реплики от ПФП 2³.

В табл. 12.7 приведён этот план, построенный с помощью следующих генераторов: x₄= x₁x₂; х₅ =x₁x₃; х₆ = х₂ х₃; х₇ = x₁x₂ x₃.

С помощью такого плана можно получить линейную модель

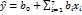(12,10)

однако нельзя проверить адекватность такой модели, так как план 2^7-4 является насыщенным.

Насыщенные дробные факторные планы часто используют в качестве планов отсеивающего эксперимента, основная цель которых не построение адекватной модели, а выявление важнейших переменных из числа варьируемых факторов.

Таблица12.7

ДФП2^{7 - 4}

2. Понятие истинного значения измеряемой статистической величины и его определение при изучении параметров оперативно – тактических действий.

Сплошное обследование всех элементов генеральной совокупности может потребовать больших затрат средств и времени. По этой причине исследователь всегда имеет дело с выборочной статистической совокупностью, то есть с частью общей генеральной совокупности.

Однако исследователя прежде всего интересуют свойства всей генеральной совокупности. Поэтому одна из важнейших задач математической статистики заключается в определении параметров всей генеральной совокупности на основании информации, которую можно извлечь из ограниченной выборки. Поясним сказанное примером. Пусть нас интересует среднее время развертывания насосно-рукавной системы для забора воды насосной установкой мобильного средства пожаротушения расчетом из двух человек какого либо гарнизона пожарной охраны. Мы, конечно, можем провести прием зачетов от исполнителей в каждом карауле всех пожарных частей этого гарнизона пожарной охраны и таким образом совершенно точно найти среднее время развертывания двумя исполнителями заранее оговоренных условиях – генеральное среднее M_y.

Однако такое сплошное обследование всей генеральной совокупности потребует больших затрат средств и времени. Поэтому в практике применяют выборочный метод, с помощью этого метода среднее время находят не по всем караулам - всей генеральной совокупности, а по их небольшой части - выборке.

Допустим, для простоты, что весь гарнизон состоит из девяти пожарных частей, которые при развертывания насосно-рукавной системы для забора воды из водоисточника показали следующие результаты 40, 32, 50, 46, 26, 30, 22, 36 и 48 с. Легко подсчитать, что генеральное среднее М_у этой статистической совокупности равно 36,6 с.

Проведем теперь выборочное измерение времени выполнения упражнения по трем произвольно взятым группам исполнителей. Для этого выберем какие-либо три результата (например, первые три) и найдем их среднее значение ₁:

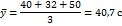
Если бы мы возьмём следующие три измерения - 46, 26, 30, - то получили бы уже другое значение выборочного среднего: ₂ = 34,0 с. В первом случае ошибка - разность между выборочным средним и действительным значением среднего времени - равнялась ₁ -М _у = 40,7- 36,6 = 4,1 с;во втором ₂-М_у = 34,0 -36,6 = - 2,6 с.

Как видим, определение генерального среднего по выборочному производится с ошибкой. Каждое из возможных выборочных значений (в качестве обследуемых мы могли взять произвольным образом любые три измерения) находится как среднее арифметическое трех случайных величин. Соответственно выборочное среднее также является случайной величиной. Эта случайная величина в ту или иную сторону отклоняется от истинного среднего значения генеральной совокупности.

Точно так же и другие выборочные параметры (например, выборочная дисперсия) являются случайными величинами. Их отклонения от генеральной совокупности случайны. Следовательно, можно указать только вероятность того или иного отклонения и тем самым охарактеризовать численно надежность (достоверность) полученного результата. Вероятность р нахождения истинного значения параметра генеральной совокупности в некоторых пределах называется доверительной вероятностью. Пределы, соответствующие доверительной вероятности, называют доверительными границами, а образуемый ими интервал - доверительным интервалом.

Техника нахождения доверительного интервала для генерального среднего несложна. При выборке объема n< 120 закон распределения ошибки - разности между генеральным и выборочным средним - описывается известной функцией распределения, называемой t -распределением Стьюдента. Используя свойства этого распределения, можно всегда вычислить вероятность отклонения выборочного среднего от генерального на данную величину. Соответственно можно найти и доверительный интервал.

Для расчета доверительного интервала необходимо. Найти выборочное среднее у и оценку дисперсииs².Задаться уровнем значимости q. Уровнем значимости называют вероятность ошибки, которой допустимо пренебречь в данном исследовании. В нашем случае ошибка будет заключаться в том, что генеральное среднее М_у не будет лежать внутри найденного интервала. Поэтому q = 1 -р. Обычно в технологических расчетах величину доверительной вероятности р берут в пределах от 0,9 до 0,99.

Для данного уровня значимости q и числа степеней свободы f = n - 1 из Приложения 4находят величину t_qf. Расчет доверительного интервала производится по формуле:

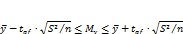(8.15)

П ример. В результате серии экспериментов из n = 30 испытаний были получены следующие значения: = 28,2 с, S² = 36. Требуется определить доверительные границы для среднего значения, соответствующие 95%-ной доверительной вероятности.

Решение. Для доверительной вероятности р = 0,95 уровень значимости q = 1 - - 0,95 = 0,05. Число степеней свободы f = 30 - 1 = 29. Из Приложения находим для данных значений q и f значение t_qf = 2,04. Подставляя полученные результаты в формулу (8.15), получаем 28,2 - 2,04 1,09 ≤ М_y ≤ 28,2 + 2,04 1,09, или, окончательно, 26,02 ≤ M_y ≤ 30,42.

Таким образом, с вероятностью 0,95среднее значение заключено между 26,02 с и 30,42 с. То есть из 100 выполненных произвольных экспериментов 95 будут иметь среднее время, лежащее в найденном интервале.

Дата добавления: 2014-11-25