
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Оптимизация оперативно-тактических действий. Математическая модель оптимизации для двух исполнителей
|
|
|
|
Показатели работоспособности
Таблица 10.2
| Возраст, лет | Физическая работоспособность, кг м/мин/кг | |||
| Пониженная (1) | Средняя (2) | Высокая (3) | Очень высокая (4) | |
| 20-29 | <16.2 | 16.2-19.3 | 19.3-20.9 | >20.9 |
| 30-39 | <14.9 | 14.9-17.9 | 17.9-19.1 | >19.1 |
| 40-49 | <13.4 | 13.4-16.4 | 16.4-17.9 | >17.9 |
| 50-59 | <12.0 | 12.0-14.9 | 14.9-16.4 | >16.4 |
Кого же оставляют для участия в экспериментах? Как правило для участия в экспериментах для определения различных параметров ОТД рекомендуется выбирать испытуемых с показателем группы средней и высокой физической работоспособности.
Так как считается, что участники экспериментов с низкой и очень высокой работоспособностью исказят реальное соотношение работоспособности и полученных временных параметров ОТД.
При введении оперативно-тактических действий пожарными подразделениями одним из главных условий эффективности является время их выполнения. Которое на прямую зависит от правильной расстановки исполнителей О.Т.Д. и закрепление за ними выполняемых операций в соответствии с их возможностями, знаниями и навыками их выполнения – что и называется оптимизацией с целью получения минимального времени с наименьшими затратами труда и ресурсного обеспечения.
Последовательность оптимизации оперативно-тактических действий включает:
-описание оперативно-тактического действия и условий его выполнения;
-анализ литературных источников и наработок практики;
-расчленение оперативно-тактического действия на элементы его составляющие;
-закрепление элементов оперативно-тактического действия за исполнителями;
-определение времени выполнения каждого элемента оперативно-тактического действия.
Общее время выполнения закрепленных элементов оперативно-тактических действий за исполнителями должно быть по возможности одинаковым, то есть это время ни каким образом уменьшить нельзя.
Таким образом для оптимизации оперативно-тактических действий необходимо иметь время выполнение составляемого его элемента. Время выполнения может быть известно из ранее полученных значений в других случаях его необходимо определять.
Предлагается два подхода к определению неизвестного времени выполнения элементов оперативно-тактических действий. Первый с использованием методов математической статистики, второй с использованием микроэлементных нормативов.
После определения: времени выполнения каждого элемента оперативно-тактических действий, условий проведения составляется возможность оптимизировать время его выполнения с разработанных математических моделей трудового процесса. Разработанное модель, позволяет рассмотреть различные варианты органов защиты труда, не ставя реальные опыты и выбрать оптимальные схемы.
Однако для многих актуальных задач по оптимальной организации труда исполнителей оперативно-тактических действий трудно построить математическую модель, дает точно широко и точно отражающую структуру реального процесса оперативно-тактических действий.
Рассмотрим построение модели на простом примере. Предположим что необходимо решить задачу разделения операций оперативно-тактических действий между двумя исполнителями.
При проведении оперативно-тактических действий выполняется ряд работ (операций) различной трудоемкости, и их последовательность может быть относительно произвольной. Необходимо найти такое закрепление операций и их порядок выполнение между двумя исполнителями, при котором они были бы выполнены в кратчайший срок.
Введем обозначения. i - произвольная работа, требующая выполнения (i=1,2,…,n) ti,- время выполнения i-й работы;  и
и  - специальные переменные, равные 0 или 1. Если первый исполнитель будет выполнять i-ю работу, то
- специальные переменные, равные 0 или 1. Если первый исполнитель будет выполнять i-ю работу, то 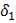 =1 и
=1 и 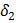 =0. Если же второй будет выполнять i-ю работу, то
=0. Если же второй будет выполнять i-ю работу, то 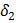 =1,
=1, 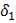 =0. Очевидно, что переменных;
=0. Очевидно, что переменных;  и
и  всего 2n.
всего 2n.
Если использовать переменные 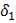 , то время работы первого исполнителя (
, то время работы первого исполнителя ( ) равно:
) равно:
 (14.9)
(14.9)
Второго – 
Минимизация производственного цикла двух исполнителей эквивалента минимизации разности 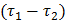 . Следовательно, в данном случае критерии эффективности (Z), выраженный совокупностью переменных, учитывающих возможные способы распределения, выполняемых операций, примет вид:
. Следовательно, в данном случае критерии эффективности (Z), выраженный совокупностью переменных, учитывающих возможные способы распределения, выполняемых операций, примет вид:
 (14.10)
(14.10)
По условию задачи каждая работа должна быть выполнена одним из исполнителей и не может выполнятся одновременно двумя исполнителями. Это условие равносильно справедливости равенств  для всех i. Любая работа i будет выполнена одним исполнителем, потому что в силу равенств либо
для всех i. Любая работа i будет выполнена одним исполнителем, потому что в силу равенств либо  (тогда
(тогда 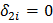 ), либо
), либо 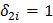 (тогда
(тогда 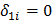 ).
).
Записав вместе критерий эффективности и ограничение, налагаемые на переменные  и
и  и получим:
и получим:
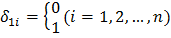 (14.11)
(14.11)
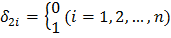 (14.12)
(14.12)
 (14.13)
(14.13)
 (14.14)
(14.14)
Совокупность выражений (14.11 – 14.14) является математической моделью описанного выше трудового процесса, формальной постановкой задачи, которая заключается к минимизации выражения (14.14) при условиях, выраженных формулами (11.11 – 11.13), то есть в определении таких значений переменных  и
и  , которые дали бы минимум Z.
, которые дали бы минимум Z.
Набор значений переменных, приводящих к минимуму (3/5) – это оптимальное решение поставленной задачи. Если,например, будет получено  ,
, 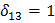 ,
,  ,то работы 1 и 3 должны выполнятся первым исполнителем, работа 2 –вторым и так далее.
,то работы 1 и 3 должны выполнятся первым исполнителем, работа 2 –вторым и так далее.
Уравнение (14.11), (14.12) и (14.13) отражают структуру трудового процесса, т.е. выражают то главное, что характеризуют распределение работ. Ни одно из уравнений не может быть опущено, так как это приведет к искажению структуры трудового процесса ОТД (например, окажется возможным выполнение одной и той же работы одновременно двумя исполнителями).
Разработка моделей заключается в поиске такого способа описания, который способствует проведению количественного анализа трудового процесса ОТД. Истинная строгость решения характеризуется не применением некоторых символов, а совпадением структур трудового процесса и математической модели. Структура последней – это совокупность соотношений, которые связывают использованные в ней переменные.
В соотношениях математической модели присутствуют не только вводимые перемены, но и еще некоторые символы – параметры модели. Для построенной модели распределение работ параметрами являются общее число работ (n) и время выполнения работ(τ₁). Определенный набор значений всех параметров представляется собой массив исходных данных. Например, если бы данная задача заключалась в распределении пяти работ, то параметр n в массиве исходных данных имел бы значение 5 (n=5).
Следует различать параметры модели и её переменные: при решении задачи массив исходных данных, т.е. определенный набор значений параметров заранее указывается (параметры фиксируются), а для переменных лишь ограничиваются области их изменения, в которых они могут принимать любые значения.
Смысл совокупности переменных заключается в указании всех допустимых организационных мероприятий при фиксированных параметрах, а при изменении значений последних этот смысл не меняется. Но как все множество решений, так и оптимальное изменяется в зависимости от исходных данных задачи. Значения параметров не являются произвольными, и множество допустимых значений каждого определяются смыслом задачи. Так, было бы ошибкой указать, что n=-5, или что время выполнения некоторой работы – отрицательное число.
Математические модели, построение которых осуществляется при решении задачи организации оперативно-тактических действий, можно разделить на две группы: детерминированные и вероятностные, что соответствует двум видам структуры трудовых процессов – детерминированному и вероятностному.
Различие этих групп моделей заключается в следующем:
для детерминированных групп моделей можно фиксировать переменные, в результате чего критерий эффективности приобретает определенное значение, для вероятностных групп часть переменных является случайными величинами, и критерий эффективности обычно выражают через средние значения этих величин, в этом случае необходимо знать распределение вероятностей каждой случайной величины, которая определяется теоретическим или экспериментальным путем.
|
|
|
|
|
Дата добавления: 2014-11-25; Просмотров: 1127; Нарушение авторских прав?; Мы поможем в написании вашей работы!