Эту избыточность можно устранить, если перейти к кодированию достаточно большими блоками

Пример20: Рассмотрим процедуру эффективного кодирования по методике Шеннона - Фано сообщений, образованных с помощью алфавита, состоящего всего из двух знаков x₁ и x₂ с вероятностями появления соответственно Р(х₁) = 0,9; P(x₂) = 0,1.

Так как вероятности не равны, то последовательность из таких букв будет обладать избыточностью. Однако, при побуквенном кодировании мы никакого эффекта не получим. Действительно, на передачу каждой буквы требуется символ либо 1, либо 0, в то время как энтропия равна

,

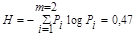т.е. оказывается

При кодировании блоков, содержащих по две буквы, получим коды:

Таблица 3.4.

Блоки	Вероятности	Кодовые комбинации
номер разбиения
x1x1	0,81
x1x2	0,09
x2x1	0,09
x2x2	0,01

Так как знаки статистически не связаны, вероятности блоков определяют как произведение вероятностей составляющих знаков.

Среднее число символов на блок

а на букву 1,29/2 = 0,645, т.е. приблизилось к Н = 0,47 и таким образом удалось повысить эффективность кодирования.

Кодирование блоков, содержащих по три знака, дает еще больший эффект:

Таблица 3.5.

Блоки	Вероятность Pi	кодовые комбинации
номер разбиения
x1x1x1	0,729
x2x1x1	0,081
x1x2x1	0,081
x1x1x2	0,081
x2x2x1	0,009
x2x1x2	0,009
x1x2x2	0,009
x2x2x2	0,001

Среднее число символов на блок равно 1,59, а на знак - 0,53, что всего на 12% больше энтропии.

Следует подчеркнуть, что увеличение эффективности кодирования при укрупнении блоков не связано с учетом все более далеких статистических связей, т.к. нами рассматривались алфавиты с независимыми знаками.

Дата добавления: 2014-11-25