Теоретические основы симплекс-метода 1 страница

Контроль знаний

1. Относительно чего должно быть принято основное управляющее решение? Какая про-блема при этом решается?

2. Почему в реальной действительности условия, в которых приходится принимать управляющие решения, настолько сложны, что возникает необходимость в использова-нии оптимизационной модели?

3. Какие факторы, характеризующие условия, учитываются в оптимизационной модели, а какие из них не принимаются во внимание?

4. В чем состоит различие между решением, имеющим практическую ценность, и реше-нием, которое не может быть реализовано?

5. Чем отличается плохое решение от хорошего?

6. Как применить результаты проведенного моделирования на практике?

7. Каким образом можно (или нужно) было бы подправить или видоизменить результаты моделирования за счет факторов, не учтенных моделью в явном виде?

8. Опишите блочную структуру построения задачи линейного программирования на ра-бочем листе электронных таблиц.

9. Дайте структурную характеристику основному диалоговому окну Поиска решения. 10.Назовите основные резолюции окна результатов Поиска решения.

11.Как указать метод решения задач линейного программирования в Поиске решения. 12.Ссылки на какие ячейки (диапазоны ячеек) рекомендуется указывать в окне ввода ог-

раничений средства Поиск решения?

Лабораторная работа № 3

Тема: Решениезадачлинейногопрограммированиясимплекс-методомЦельработы:

ƒ научиться строить каноническую форму задачи линейного программирования; ƒ выработать навыки построения начального (исходного) плана задачи;

ƒ освоить алгоритм симплекс-метода. Времяработы: 4 часа

Задание

1. Построить начальный (исходный) план задачи линейного программирования; 2. Решить задачу симплекс-методом.

Идея симплекс-метода состоит в целенаправленном переборе вершин многогранни-ка ОДР. При этом вершины ОДР представлены набором векторов, ее образующих. Век-торный набор вершины называется базисом. Остальные вершины выражаются в виде про-екций своих векторов на этот базис. Векторный базис еще называется Планом. Любой план предусматривает только уравновешенные связи между переменными задачи. Поэтому сис-тема ограничений должна содержать только уравнения, т.е. иметь каноническую форму.

Канонической формой задачи линейного программирования называется такая фор-ма, в которой все ограничения являются уравнениями, а на переменные накладывается граничное условие их неотрицательности.

Векторный базис должен:

− содержать число векторов по количеству уравнений в системе ограничений; − совокупность базисных векторов представляет собой единичный вектор.

Начиная с исходной вершины, выполняется переход в смежную вершину за счет векторной замены: вектор, соответствующий направлению перехода, входит в состав бази-са (его называют направляющим); вектор, обеспечивающий разрыв связей с предыдущими смежными вершинами, покидает базис (его называют разрешающим). Критерий необхо-димости векторной замены – это разность между приращением целевой функции по вы-бранному вектору Zj и ценовой характеристикой этого вектора Cj, т.е. разность Zj – Cj. По-рядок применения критерия (Zj – Cj) закреплен в следующих теоремах.

Теорема 1. Если в задаче на максимум есть хотя бы один вектор, чья оценка отрицатель-ная (Zj – Cj < 0), то план можно улучшить за счет ввода данного вектора в состав базиса.

Следствие 1. Если в задаче на максимум оценки всех векторов неотрицательные (Zj – Cj ³ 0), то найден оптимальный план.

Теорема 2. Если в задаче на минимум есть хотя бы один вектор, чья оценка положитель-ная (Zj – Cj > 0), то план можно улучшить за счет ввода данного вектора в состав базиса задачи.

Следствие 2. Если в задаче на минимум оценки всех векторов неположительные (Zj – Cj £ 0), то найден оптимальный план.

Выбор разрешающего вектора идет после выбора направляющего вектора. Он может заключаться в выборе наименьшего (минимального) приращения по базису: критерий от-ношения q min { Bi / xij }.

Самым удобным способом рассмотрения векторного пространства задачи относи-тельно базиса считается табличный способ. Базисные вектора представляют собой строки, все вектора пространства задачи – столбцы. Таким образом, векторная замена в табличном способе представления – это замена по строке с обязательным пересчетом коэффициентов проекции всех векторов. На пересечении разрешающей строки (вектор, покидающий ба-зис) и направляющего столбца (вектор, поступающий в состав базиса) лежит генеральный элемент таблицы, через который осуществляется пересчет.

Пересчет выполняют по следующим правилам:

ì

ï

í

ï

ì

ï

í

ï

1. Все элементы (коэффициенты проекции векторов) разрешающей строки делятся на ге-неральный элемент.

2. Направляющий столбец становится ортом (элементом единичного вектора).

3. Коэффициенты (элементы) остальных строк таблицы пересчитываются через гене-ральный элемент.

Существуют различные варианты пересчета. Самый наглядный из них – это мнемо-нический прямоугольник Жордано-Гаусса. В его основе лежит связь пересчитываемого элемента с генеральным.

Прямоугольник строится следующим образом. Пересчитываемый элемент соединя-ется с генеральным по диагонали. Две другие вершины определяем по строке и столбцу.

Новое значение пересчитываемого элемента равно предыдущему минус приращение прямоугольника. Приращение прямоугольника определяется как отношение: в числителе произведение двух других вершин прямоугольника; в знаменателе – генеральный элемент.

На основании прямоугольника Жордано-Гаусса легко можно реализовать единую расчетную формулу для электронных таблицах Excel.

Вычислительный процесс прекращается после выполнения условий, описанных в следствиях к теоремам оптимальности.

Примеррешениязадачи Дана следующая задача линейного программирования

Z =15 x +14 x 2+12 x 3® max

10 x + 7 x 2+3 x 3£ 210 8 x +5 x 2+ 2 x 3£120

î x ³ 0 x 2³ 0 x 3³ 0

.. (3.1)

Требуется решить данную задачу симплекс-методом. Решение

1. Приведем задачу к канонической форме. Для этого в каждое неравенство добавим до-полнительные переменные с таким расчетом, чтобы уравновесить между собой левую и правую части выражений. В 1-ое неравенство введем х 4, во второе введем х 5. В целе-вую функцию дополнительные переменные должны войти с нулевым коэффициентом.

Z =15 x +14 x 2+12 x 3 0 x 4 0 x 5® max

10 x + 7 x 2+3 x 3+ x 4 = 210 8 x +5 x 2+ 2 x 3 + x 5=120

î x ³ 0 x 2³ 0 x 3³ 0 x 4³ 0 x 5³ 0

. (3.2)

2. Векторный базис должен состоять из линейно независимых переменных. Имеем две линейно независимые переменные х 4 и х 5. То есть в состав базиса войдут два вектора по числу уравнений-ограничений. Переходим к построению симплекс-таблицы.

3. В таблицу записываем уравнения задачи (табл.3.1). Вариант записи в электронной таб-лице Excel показан на рисунке (рис.3.1). Заметим, что он отличается от нижерасполо-женной таблицы, так как на рабочем листе не рекомендуется выполнять объединение ячеек.

Таблица 3.1. Симплекс-таблица с уравнениями

Базис	Cб						B
x1	x2	x3	x4	x5
x4
x5
Zj-Cj

4. Переходим к расчету критерия Zj – Cj. Zj – это сумма произведений ценовых коэффи-циентов базисных векторов (Сб) на коэффициенты разложения j -го вектора по базису. Так как ценовые коэффициенты базисных векторов – величина постоянная, то для них

следует использовать абсолютную адресацию. На рисунке 3.1 в ячейку С5 вводится формула: =СУММПРОИЗВ($B$3:$B$4;C3:C4)-C1, которая копируется по строке.

Таблица 3.2. Симплекс-таблица с оценками векторов

Базис	Cб						B
x1	x2	x3	x4	x5
x4
x5
Zj-Cj	-15	-14	-12

5. Выбираем вектор, который должен войти в состав базиса. Имеем 3 вектора с отрица-тельной оценкой (Zj – Cj < 0). Выбираем вектор, который имеет наибольшую по абсо-лютной величине отрицательную оценку: это вектор х 1 (табл.3.2). Он должен войти в состав базиса. Столбец вектора х 1 – направляющий.

6. Определяем вектор, который будет покидать базис. Для этого используем критерий оценки: q min = min { Bi / xij }. Делим значения, представленные в столбце В (табл3.3) на коэффициенты направляющего столбца.

Таблица 3.3. Симплекс-таблица после определения генерального элемента

Базис	Cб						B	q
x1	x2	x3	x4	x5
x4
x5
Zj-Cj	-15	-14	-12

7. Минимальное приращение по базису имеет вектор х 5. Он будет покидать базис. Строка вектора х 5 разрешающая (табл.3.3).

8. На пересечении разрешающей строки и направляющего столбца находится генераль-ный элемент. Его значение равно 8.

9. Копируем шапку таблицы (рис.3.1).

10.Вписываем в состав базиса вектора (х 4 и х 1) и их ценовые коэффициенты (0 и 15). Таблица 3.4. Симплекс-таблица после векторной замены

Базис	Cб						B
x1	x2	x3	x4	x5
x4
x1
Zj-Cj

11.Для заполнения новой таблицы (табл.3.4) следует использовать формулы пересчета. Используем прямоугольник Жордано-Гаусса.

12.Строка таблицы х 4 не является разрешающей. Поэтому строим в ней формулу прямо-угольника (рис.3.1). Выбираем ячейку Н9 (столбец свободных членов уравнения В). Зрительно строим мнемонический прямоугольник. Ячейку Н3 (значение 210) соединя-ем диагональю с генеральным элементом (ячейка С4 – значение 8), две других верши-ны ищем по столбцу (ячейка Н4 – значение 120) и строке (ячейка С3 – значение 10). Так как новое значение пересчитываемого элемента равно его предыдущему значению за вычетом произведения элементов других вершин, деленному на генеральный эле-мент, то реализуем формулу: = Н3 – Н4 * С3 / С4 или вычисляем (табл.5)

210−120×10 = 210−150 = 60.

При переходе к расчетам в таблице Excel следует один раз ввести формулу, а затем скопировать ее по строке. Поэтому будем использовать правило расчетов.

Правило. Все ячейки, находящиеся в направляющем столбце, должны иметь абсолютный адрес.

Поэтому формула в ячейке Н9 следует ввести формулу =H3-H4*$C$3/$C$4. Копируем ее по строке влево (рис.3.1).

Строка таблицы х 3 является разрешающей. Поэтому строим в ней формулу деления эле-ментов строки на генеральный элемент. Используем то же правило: генеральный элемент имеет абсолютный адрес, Н10 =H4/$C$4. Копируем ее по строке влево (рис.3.1).

Таблица 3.5. Симплекс-таблица после пересчета

Базис	Cб						B
x1	x2	x3	x4	x5
x4			3/4	1/2		-1 1/4
x1			5/8	1/4		1/8
Zj-Cj

13.Для того чтобы определить оптимальность плана, рассчитываем критерий Zj – Cj. На рисунке 3.1 в ячейке С11 вводится формула =СУММПРОИЗВ($B$9:$B$10;C9:C10)-C7, которая затем копируется по всей строке.

Таблица 3.6. Симплекс-таблица после первой итерации

Базис	Cб						B
x1	x2	x3	x4	x5
x4			3/4	1/2		-1 1/4
x1			5/8	1/4		1/8
Zj-Cj		-4 5/8	-8 1/4		1 7/8

14.Имеем два вектора с отрицательной оценкой (х 2 и х 3). План можно улучшить (теорема оптимальности). В качестве направляющего столбца выбираем вектор х 3 (наибольшая по абсолютной величине отрицательная оценка).

15.Определяем вектор, который будет покидать базис. Для этого используем критерий оценки: q min = min { Bi / xij }. Минимальное приращение по базису имеет вектор х 1. Он будет покидать базис. Строка вектора х 1 разрешающая. Значение генерального элемен-та равно 1/4.

Таблица 3.7. Симплекс-таблица с генеральным элементом

Базис	Cб						B	q
x1	x2	x3	x4	x5
x4			3/4	1/2		-1 1/4
x1			5/8	1/4		1/8
Zj-Cj		-4 5/8	-8 1/4		1 7/8

16.Копируем шапку таблицы (рис.3.1). Записываем в состав базиса вектора х 4 и х 3. 17.Для пересчета таблицы формируем следующие формулы:

− ячейка Н15: =H9-H10*$E$9/$E$10 (прямоугольник Жордано-Гаусса); − ячейка Н16: =H10/$E$10 (разрешающая строка).

Таблица 3.8. Итоговая симплекс-таблица

Базис	Cб						B
x1	x2	x3	x4	x5
x4		-2	- 1/2			-1 1/2
x3			2,5			0,5
Zj-Cj

18.Рассчитываем строку оценок: С17 =СУММПРОИЗВ($B$15:$B$16;C15:C16)-C13. 19.Строка включает только неотрицательные оценки (Zj – Cj ³ 0), то есть найден опти-

мальный план.

20. Ответ: Zmax = 720; х 1 = 0 (не входит в состав базиса); х 2 = 0 (то же); х 3 = 60.

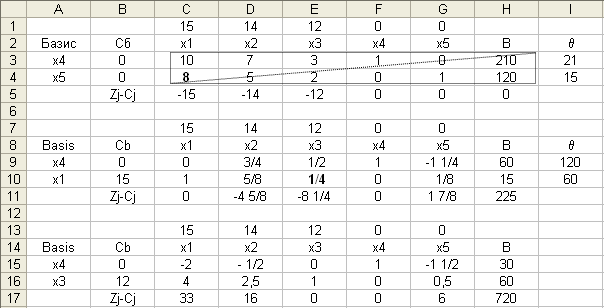Рисунок 3.1 Расчет симплекс-методом в Excel

Вариантызаданий

№ вар.	Задачи		№ вар.	Задачи		№ вар.	Задачи		№ вар.	Задачи		№ вар.	Задачи
	11 22			14 21			4 19			1 26			2 26
	7 29			5 17			12 23			7 18			8 30
	6 27			2 24			13 18			15 21			1 17
	4 25			13 22			10 19			5 29			9 16
	3 24			9 28			14 25			3 20			10 20
	15 16			8 28			6 27			12 23			11 30

Задачи 1 – 30

Найти решение линейной оптимизационной модели симплекс-методом в Excel.

Z = 4 x + 7 x 2+8 x 3® max Z = 5 x +3 x 2 5 x 3® max Z = 4 x +9 x 2+3 x 3® max

ì4 x + 6 x 2+3 x 3£ 27 í2 x +5 x 2+8 x 3£ 24 î1³ 0, x 2³ 0, x 3³ 0

Z = 6 x +8 x 2+3 x 3® max

ï

í

ì4 x + 6 x 2+3 x 3£ 26 8 x + 2 x 2+3 x 3£ 27

x

î1³ 0, x 2³ 0, x 3³ 0

Z = 3 x +3 x 2+ 4 x 3® max

Дата добавления: 2014-11-25