Задачи по теме: «Плоская система произвольно расположенных сил». Определение опорных реакций, исходя из условия равновесия в аналитической форме

Записать уравнения равновесия в аналитической форме, исходя из заданной расчётной схемы конструкции.

Первая форма уравнений равновесия состоит из системы трёх уравнений равновесия:

SХ_i=0 -сумма проекций всех действующих сил на ось ОХ равна 0.

SY_i=0 -сумма проекций всех действующих сил на ось ОY равна 0.

SМ_А=0 – сумма моментов всех действующих сил относительно любой точки, например точки А- центра моментов, равна 0.

Проверочное уравнение SМ_В=0

Вторая форма уравнений равновесия состоит из системы трёх уравнений равновесия, в которой одно из уравнений проекций меняем на уравнение моментов. В качестве уравнения проекций выбирается любая ось кроме перпендикуляра к прямой проходящей через центры моментов.

SХ_i=0 -сумма проекций всех действующих сил на ось ОХ равна 0.

S М_А =0 -сумма моментов всех действующих сил относительно точки А =0.

SМ_В=0 – сумма моментов всех действующих сил относительно точки В =0

Проверочное уравнение SY_i=0

Конструкции в виде консоли, имеющие одну точку опоры лучше решать по первой форме уравнений равновесия.

Балки на двух опорах лучше решать по второй форме уравнений равновесия. Две точки опоры – два уравнения моментов.

Первая форма уравнений равновесия является более универсальной, так как не имеет никаких ограничений на составление уравнений проекций.

Задача №1: Определить реакции связи в точке А.

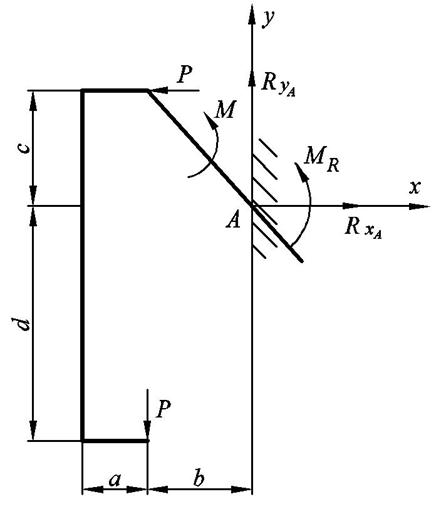
Р=18 кН,

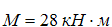
а= 3 м, b= 3 м, с =7 м, d= 2 м.

Решение. Изображаем реакции связей в точке А: R_YA, R_XA, М_R.

Положительное направление М_R - против часовой стрелки.

Выбираем плоскую декартовую систему координат. Ось ох вправо, ось оу вверх.

Выбираем первую форму уравнений равновесия. Проецируем действующие силы

SХ_i=R_XA + Р=0

SY_i=R_YА=0

SМ_А=М_R – М - Р∙с=0

SХ_i=R_XA = - Р= -18 кН

SY_i=R_YА=0

SМ_А=М_R = М+ Р ∙ с=28+18∙7=154 кН∙м

Проверочное уравнение

SМ_В= М_R – М - R_YА ∙ а + R_XA ∙ с = 154 – 28 - 0∙3 - 18∙7=0

Ответ: реакции связей в точке А R_XA = -18 кН; R_YА=0; М_R=154 кН∙м

Задача №2: Определить реакции связи в точках А.

Р=18 кН, М=17 кН∙м, а= 3 м, b= 1 м, с=2 м.

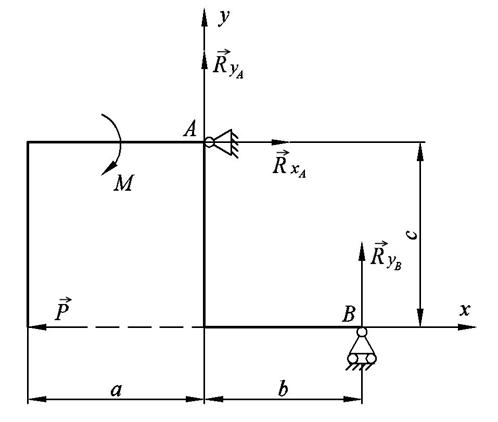
Решение. Изображаем реакции связи в точках А и В: R_YA, R_XA, R_YВ.

В точке А опора шарнирно-неподвижная - две реакции связи R_YA, R_XA,

в точке В опора шарнирно-подвижная – одна реакция связи R_YВ.

Выбираем вторую форму уравнений равновесия

SХ_i= R _ХА – Р=0

S М_А = - М - Р ∙с + R_YВ ∙ b = 0

SМ_В= - М - R_YА ∙ b - R_XA ∙ с = 0

Проверочное уравнение SY_i=0

SХ_i= R _ХА = Р =18 кН

Проверка:

SY_i=0

R_YA + R_YВ= -53 + 53 = 0

Ответ: R _ХА=18 кН; R_YА= -53 кН

Дата добавления: 2014-11-25