Решение. 1. Для построения дискретного вариационного ряда необходимо подсчитать количество появления каждой оценки

1. Для построения дискретного вариационного ряда необходимо подсчитать количество появления каждой оценки, т.е. частоту появления признака. Дискретный ряд представлен в таблице 5.1.

Таблица 5.1

Распределение студентов по успеваемости

Успеваемость (балл), х	Число сту- дентов, f	Накопленные частоты, S нак	x f	x^2 f
					88,875
					15,787
					0,086
					1,8136
					46,3333
Итого		-			152,8949

2. Графически дискретный вариационный ряд может быть представлен в виде полигона (рис.5.1), кумуляты (рис.5.2) распределения. Полигон строится в прямоугольной системе координат.

По оси абсцисс откладываются значения дискретного признака, а по оси ординат – частоты распределения. Полигон часто замыкается, - для этого крайние вершины соединяются с точками на оси абсцисс, отстоящими на одно деление в принятом масштабе (в данном примере х = 0 и х = 6).

Кумулята – это линейный график накопленных частот. Для построения кумуляты дополнительно рассчитываются накопленные частоты (S_НАК), - они представлены в таблице 5.1, и в прямоугольной системе координат строится их график (рис.5.2).

Рис. 5.2. Кумулята распределения студентов по успеваемости

3. Cтруктурными средними выступают мода и медиана.

Модальное значение признака, т.е. М_о = 4 (балла). Графически – это вершина полигона распределения (рис.5.1).

Медиана равна 3 балла, так как S_НАК = =15 для признака, равному 3. Графически медиана определяется с помощью кумуляты распределения. Для ее определения сумму ординат (сумму частот) делят пополам, т.е. . Через полученную точку проводится прямая параллельно оси абсцисс до пересечения ее с кумулятой. Абсцисса точки пересечения является медианной величиной распределения (рис. 5.2).

3. Для оценки формы распределения исчислим коэффициент асимметрии и эксцесса: ; (балла); М₀ =

= 4(балла); ; .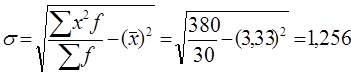

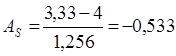, это свидетельствует о наличии левосторонней асимметрии распределения студентов по успеваемости (рис. 5.1).

Для проверки статистической гипотезы о существенности асимметрии рассчитываем соотношение 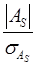, исчислив предварительно: = ; .

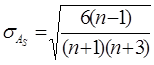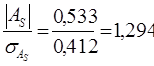
В нашем примере наличие асимметрии несущественно и объясняется влиянием случайных факторов.

Исчислим коэффициент эксцесса: ; =

; .

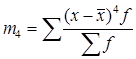Так как , то распределение студентов по успеваемости – низковершинное или плосковершинное по сравнению с нормальным распределением.

5. Для проверки гипотезы о соответствии эмпирического распределения нормальному используем критерий Пирсона или - критерий. Определим теоретические частоты нормального распределения по формуле: ; ; h = 1 (для дискретного ряда); n = ∑ f = 30, тогда .

Все промежуточные расчеты представлены в таблице 5.2.

Определяем расчетное значение -критерия: =2,1146. Полученное значение =2,1146 сравнивается с табличным значением 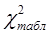, которое определяется по заданной вероятности (например, Р = 0,95) и числу степеней свободы (m = k – 3 = 5 - 2) (приложение 4).

Таблица 5.2

Вспомогательные расчеты теоретических частот нормального

закона распределения

Успеваемость, (x)	Число студентов, (f)		[2]= =	Теор.частоты,	Округл. теорет. частоты,
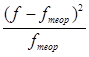
		-1,854	0,0721	1,72	2,0	0,5
		-1,058	0,2275	5,43	5,4	0,0296
		-0,262	0,3857	9,2	9,2	0,526
		0,533	0,3467	8,26	8,3	0,059
		1,328	0,1647	3,93	4,0	1,0
Итого					28,9[3]	2,1146

= 6. Так как < (2,1146 < 6,0), то гипотеза о соответствии эмпирического распределения нормальному с вероятностью 0,95 не отвергается. На рис.5.1 построим теоретическую линию нормального закона распределения. Эмпирическое распределение близко нормальному закону распределения, однако оно более плосковершинно, чем нормальное (Е_Х < 0) и с незначительной правовершинной асимметрией (А_S < 0), что видно на графическом изображении эмпирического и теоретического распределения.

Пример 2. Известно распределение коммерческих банков области по размеру прибыли.

Размер прибыли, млн.грн	До 10,0	10,0 – 20,0	20,0 - 30,0	30,0 - 40,0	40,0 - 50,0	Свыше 50,0	Ито- го
Количество банков

Оцените уровень вариации банков по размеру прибыли, рассчитав абсолютные и относительные показатели вариации. Сделайте выводы.

Дата добавления: 2014-11-25