
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Нормального распределения
|
|
|
|
Кумулятивные показатели распределения семей по среднедушевому доходу
| Среднедушевой доход, грн. | Число семей | Общая сумма среднемесячных доходов |

|

| |||||
| интервальное распределение | диск- ретное, х | кол-во семей, f | частость, %, fотн, | накоплен- ная частость, %, fcum, | гри- вен, xf | в % к итогу xотн | накоплен- ный % к итогу, xcum | ||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 130 - 150 | 5,0 | 3,42 | 3,42 | 0,00171 | 0,00171 | ||||
| 150 - 170 | 7,82 | 11,24 | 0,01124 | 0,00782 | |||||
| 170 - 190 | 17,6 | 28,84 | 0,05768 | 0,0352 | |||||
| 190 - 210 | 24,45 | 53,29 | 0,133225 | 0,061125 | |||||
| 210 - 230 | 16,1 | 69,39 | 0,104085 | 0,02415 | |||||
| 230 - 250 | 12,5 | 87,5 | 14,67 | 84,06 | 0,105075 | 0,0183375 | |||
| 250 - 270 | 12,5 | 15,94 | 0,125 | 0,0019925 | |||||
| Итого: | - | - | - | 0,538015 | 0,1500335 |
Таблица 5.6
Вспомогательная таблица для расчета теоретических частот
| Средне душевые доходы, грн. | Число семей, f | x |

| 

| Теоретические частоты, fтеор | Округленные частоты, fтеор |
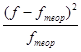
| Накопленные частоты | Разность между накопленными фактическими и теоретическими частотами | |
| фактически | теоретически | |||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 = 9 - 10 |
| 130 - 150 | -1,937 | 0,062 | 7,4462 | 7,4 | 0,9135 | 7,4 | - 2,6 | |||
| 150 - 170 | -1,336 | 0,1646 | 19,768 | 19,8 | 0,00202 | 27,2 | - 2.8 | |||
| 170 - 190 | - 0,7357 | 0,3040 | 36,63 | 36,6 | 0,3158 | 63,8 | 6,2 | |||
| 190 - 210 | 0,1351 | 0,3954 | 47,49 | 47,5 | 0,1316 | 111,3 | 8,7 | |||
| 210 - 230 | 0,4655 | 0,3585 | 43,056 | 43,0 | 3,93 | 154,3 | 4,3 | |||
| 230 - 250 | 1,066 | 0,240 | 29,06 | 29,1 | 0,578 | 183,4 | - 8,4 | |||
| 250 - 270 | 1,667 | 0,1000 | 12,06 | 12,1 | 13,75 | 195,5 | 4,5 | |||
| Итого | 195,5' | 19,62 |
Этапы решения:
- определяем теоретические частоты нормального закона распределения ( ) по формуле:
) по формуле: 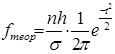 ;
; 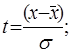
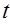 -нормированное отк-лонение;
-нормированное отк-лонение;  = 204,5 грн;
= 204,5 грн; 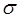 = 33,3. (Все промежуточные расчеты представлены в таблице 5.6). Общий множитель
= 33,3. (Все промежуточные расчеты представлены в таблице 5.6). Общий множитель  ;
;
- по таблицам t- распределения (приложение 3) определяем значение плотности:  ,при этом
,при этом 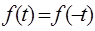 . Например, для
. Например, для 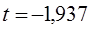 ;
;  для
для  ;
;  и т.д. Эти значения заносятся в графу 5 таблицы 5.6;
и т.д. Эти значения заносятся в графу 5 таблицы 5.6;
- определяем теоретические частоты ( ) и заносим их в графу 6, а округленные – в графу 7 таблицы 5,6; сумма теоретических частот
) и заносим их в графу 6, а округленные – в графу 7 таблицы 5,6; сумма теоретических частот  , т.е. несколько меньше 200, что объясняется округлением цифр при расчете f (t) и f теор.
, т.е. несколько меньше 200, что объясняется округлением цифр при расчете f (t) и f теор.
Для оценки степени расхождения эмпирического и теоретического распределения используется критерий Пирсона (промежуточные расчеты представлены в графе 8 табл. 5.6)  .
.
Определяем табличное значение критерия, т.е.  по заданной вероятности (
по заданной вероятности ( или 0,9) и числу степеней свободы:
или 0,9) и числу степеней свободы:  3=
3=  (см. приложение 4).
(см. приложение 4).
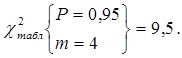 Т.к.
Т.к.  , то гипотеза о соответствии эмпирического распределения нормальному закону распределения не подтверждается.
, то гипотеза о соответствии эмпирического распределения нормальному закону распределения не подтверждается.
Для проверки этой же статистической гипотезы можно использовать критерий Романовского и критерий Колмогорова.
- Критерий Романовского:  . Если
. Если  , то гипотеза о соответствии эмпирического распределения нормальному не принимается.
, то гипотеза о соответствии эмпирического распределения нормальному не принимается.
- Критерий Колмогорова:  .
.
 - распределения определяет вероятность, т.е.
- распределения определяет вероятность, т.е. 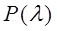
 = = 0,15 (приложение 5).
= = 0,15 (приложение 5).
Если  - значительна, т.е. близка к 1, то расхождения между эмпирическим и нормальным распределением несущественны. В нашем примере расхождения существенны, что подтверждает сделанные выше выводы.
- значительна, т.е. близка к 1, то расхождения между эмпирическим и нормальным распределением несущественны. В нашем примере расхождения существенны, что подтверждает сделанные выше выводы.
3. Построим графики эмпирического и теоретического распределения семей по среднедушевым доходам (рис.5.4):













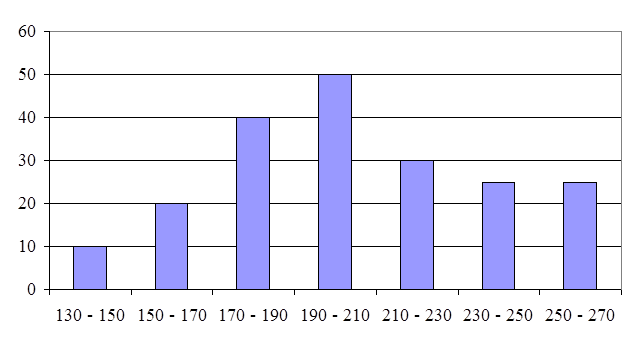 - гистограмма распределения
- гистограмма распределения
-  полигон распределения
полигон распределения
-  теоретическая линия нормального распределения
теоретическая линия нормального распределения
Рис.5.4. Распределение семей по среднедушевому доходу
Пример 5. Налоговой инспекцией одного из районов города проверено 172 коммерческих киоска и в 146 из них выявлены финансовые нарушения. Определите среднее значение, дисперсию и среднее квадратическое отклонение альтернативного признака, т.е. доли киосков, у которых выявлены финансовые нарушения.
|
|
|
|
|
Дата добавления: 2014-11-25; Просмотров: 585; Нарушение авторских прав?; Мы поможем в написании вашей работы!