Решение. 1а. Определяем структурные характеристики ряда распределе-ния, т.е

1а. Определяем структурные характеристики ряда распределе-ния, т.е. моду медиану, квартили, децили по рассмотренным выше формулам этих характеристик для интервальных вариационных рядов.

Для выбора соответствующего интервала предварительно опре-делим накопленные частоты , (табл. 5.4, гр. 4).

Модальный интервал – это интервал с наибольшей частотой 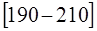, тогда 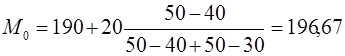грн.

Большинство семей имеют среднедушевые доходы в размере 196,67 грн. Медианным является интервал , т.к. для него первая накопленная частота больше половины объема совокупности, т.е. 120>100. Тогда медиана будет равна: 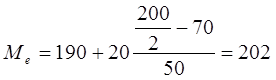грн.

Половина семей имеют среднедушевые доходы, не превышаю-щие доходы 202 грн., а у другой половины семей среднедушевые доходы, соответственно, выше 202 грн.

Интервал, в котором будет находиться первый квартиль() рас-пределения, , т.к. ему соответствует первая накопленная час-тота , большая ; а интервал, в котором находится третий квартиль(), будет 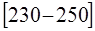, т.к. ему соответствует > .

Тогда соответствующие квартили будут равны:

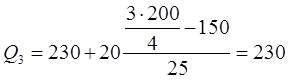грн; грн.

Среднедушевые доходы, не превышающие 180 грн., получают не менее четверти (25%) из всей совокупности семей, а в размере, не превышающем 230грн., не менее 75% всех семей.

Более детальная характеристика распределения может быть получена на основе децилей распределения. Интервалы соответствующих децилей определяются аналогично по соответствующим накопленным частотам. Например, находим первую , - это будет 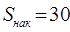; тогда соответствующий ей интервал 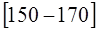будет тем интервалом, в котором находится первый дециль (d₁) – и т.д.

Рассчитаем соответствующие децили:

грн; грн;

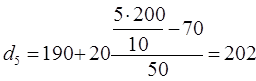грн; грн;

грн; грн;

грн; грн;

грн. Первый дециль показывает, что у 10% семей с самым низким среднедушевым доходом самый высокий размер среднедушевого дохода составляет 160 грн., а девятый дециль, - что среди 10% семей с самым высоким уровнем дохода – нижняя его граница составляет 254 грн.

1б. Анализ формы, дифференциации и концентрации распределения проводится с помощью системы специальных коэффициентов, в частности, рассчитываются:

- относительный показатель асимметрии (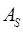), показатель эксцесса (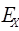), коэффициент децильной дифференциации (), индекс Джинни (К^Дж).

Дополнительно используется графическое изображение степеней неравномерности распределения вариационного ряда в виде кривой Лоренца.

Относительный показатель асимметрии исчислим как:

; грн;

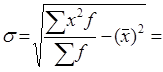
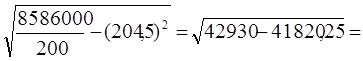33,3 грн;

.

, т.е. это свидетельствует о наличии правосторонней асим-метрии, при этом она незначительная, т.к. . Наиболее точ-ным выступает коэффициент асимметрии, рассчитанный на основе третьего центрального момента:

; ;

Для проверки существенности (или несущественности) асимметрии определяется средняя квадратическая погрешность коэффициента асимметрии(): ; ,т.е.асим-метрия несущественна в данном вариационном ряду. Так как приведенное распределение симметричное, то для таких распределений дополнительно рассчитывается коэффициент эксцесса:

; ; ; .

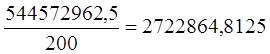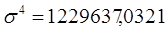Значение свидетельствует о том, что распределение низко-вершинное или плосковершинное.

Для проверки гипотезы о статистической существенности эксцес-са рассчитываем среднеквадратическую ошибку эксцесса:

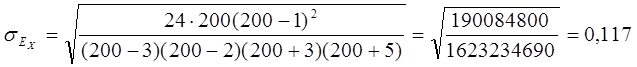_. Если , то гипотеза о статистической существенности экс-цесса не отвергается: т.е. 6,72 >3. Это подтверждает ги-потезу о статистической значимости (или существенности) эксцесса.

Для оценки степени дифференциации признака в совокупности рассчитаем коэффициент децильной дифференциации:

Это означает, что в 1,6 раза наименьший среднедушевой доход 10% семей, имеющих наибольшие доходы, больше наибольшего сред-недушевого дохода из 10% семей, имеющих самые низкие среднедуше-вые доходы.

Анализ дифференциации (или концентрации) распределения признаков основан на построении кривой Лоренца и расчета индекса дифференциации или коэффициента Джинни.

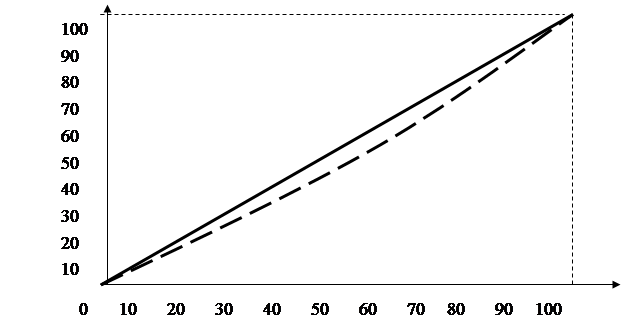
По данным таблицы 5.4 построим кумулятивные относительные показатели изучаемого признака (среднедушевого дохода) и частот (чис-ла семей), т.е. относительные показатели числа единиц в группах и раз-мерах признака (среднедушевые доходы) выражаются в относительных величинах (в долях или процентах к итогу) и определяются их накоп-ленные значения (табл.5.5, гр.5 и 8). Для построения кривой Лоренца по горизонтальной оси графика откладываются значения графы 5, а по вер-тикальной - значения графы 8, и соединение этих точек образует кривую Лоренца, характеризующую равномерность и степень концентрации распределения рабочих по уровню среднедушевого дохода (рис. 5.3).

		fсиm,%

Рис.5.3. Кривая Лоренца

Для количественной оценки меры концентрации рассчитывает-ся коэффициент концентрации Джинни:

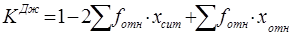= 1 – 2 · 0,538015 + 0,1500335 = 0,074.

Соотношение линий равномерного и фактического распределения (рис.5.3), а также значение коэффициента близкое к 0, свидетельствует о достаточно равномерном распределении семей по среднедушевомудоходу и, соответственно, о незначительной степени концентрации.

2. Проверяем гипотезу о соответствии эмпирического распределения семей по среднедушевому доходу нормальному закону распределения, используя критерий согласия К. Пирсона или χ² - критерий.

Таблица 5.4

Распределение семей по среднедушевому доходу

Среднеду-шевые доходы, грн	Число се- мей	Закрытые ин-тервалы сред-недушевых доходов, грн		х	xf	x ^2 f
1	2	3	4	5	6	7	8	9	10	11
До 150,0		130 - 150					- 64,5	- 2683361,25	173076800,625	41602,5
150,0 -170,0		150 - 170					- 44,5	-1762422,5	78427801,25
170,0 -190,0		170 - 190					- 24,5	- 588245	14412002,5
190,0 -210,0		190 - 210					- 4,5	- 4556,25	20503,125	1012,5
210,0 -230,0		210 - 230					15,5	111716,25	1731601,875	7207,5
230,0 -250,0		230 - 250					35,5	1118471,875	33705751,625	31506,25
Свыше 250,0		250 - 270					55,5	4273846,975	237198501,5625	77006,25
Итого								465450,0	544572962,5

Таблица 5.5

Дата добавления: 2014-11-25