
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Организация транспортно-экспедиционного обслуживания грузоперевозок
|
|
|
|
Выбор оптимального варианта перевозки грузов
Железнодорожным транспортом прибывает четыре рода грузов для перевалки на морской вид транспорта. Общий объём прибывающих грузов составляет 20000 т, из которых 8000 тонн руды, 4000 т угля, 3000 т металлов и 5000 т гравия (судовые партии). Каждый род груза перегружается на отдельное специализированное судно, грузоподъёмность которого равна объёму прибывающих партий грузов. Грузы могут перегружаться по двум вариантам: прямому (вагон-судно) и складскому (вагон-склад-судно). Перерабатывающая способность портовых транспортно-технологических мощностей позволяет за сутки осуществлять перевалку по прямому варианту только 6000 т грузов. Требуется оптимизировать процесс перевалки и распределить грузооборот таким образом, чтобы суммарная стоимость перевалки была минимальной. Стоимости перевалки каждого рода груза по вариантам представлены в табл. 4.1.
Таблица 4.1
| Судно | Род груза | Стоимость перевалки 1 т груза по вариантам, руб. | |
| судно – вагон | судно - склад - вагон | ||
| A 1 | Руда | ||
| A 2 | Уголь | ||
| A 3 | Металл | ||
| A 4 | Гравий |
Для оптимизации перевалки груза в порту необходимо определить минимум функционала
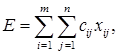 (4.1)
(4.1)
при ограничении 
где Пj – объём перевалки по j – му варианту;
ai – грузоподъёмность i - го типа судна;
ci j – себестоимость перевалки i – груза j – м способом.
Учитывая, что объём перевалки по прямому варианту составляет П1 =4600тонн, можно определить количество грузов, перегружаемых через склад
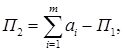 (4.2)
(4.2)
П2 = (6000 + 4000 + 2500 + 3200) – 4600 = 11100 т.
Процесс оптимизации можно осуществлять методами линейного программирования, для чего необходимо представить данные в табличной форме.
Таблица 4.2
| Род груза | Стоимость перевалки 1 т груза по вариантам, руб. | 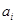 , т , т
| |
| судно – вагон | судно – склад – вагон | ||
| Руда | |||
| Уголь | |||
| Металл | |||
| Гравий | |||

|
Первоначальный план составим методом наименьшей стоимости, сущность которого состоит в том, что в клетки с наименьшей стоимостью помещается максимально возможное количество тонн для перевалки. В данной таблице минимальная стоимость в ячейке 1.1 составляет 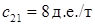 , что соответствует перевалке угля на судно по прямому варианту – в эту клетку помещаем максимально возможный объём перерабатываемого груза, второй по стоимости
, что соответствует перевалке угля на судно по прямому варианту – в эту клетку помещаем максимально возможный объём перерабатываемого груза, второй по стоимости 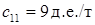 – перевалка руды по прямому варианту, помещаем в эту клетку недостающий объём столбца 6000 – 4000 = 2000 т руды и столбец 1, которому соответствует прямой вариант вагон-судно, исключаем из дальнейшего рассмотрения. Оставшуюся часть руды 8000 – 2000 = 6000 т помещаем в следующую клетку строки с минимальным значением стоимости, для данной таблицы это ячейка 1.2 со стоимостью с 12 = 15 руб/т.
– перевалка руды по прямому варианту, помещаем в эту клетку недостающий объём столбца 6000 – 4000 = 2000 т руды и столбец 1, которому соответствует прямой вариант вагон-судно, исключаем из дальнейшего рассмотрения. Оставшуюся часть руды 8000 – 2000 = 6000 т помещаем в следующую клетку строки с минимальным значением стоимости, для данной таблицы это ячейка 1.2 со стоимостью с 12 = 15 руб/т.
Для начального плана должно выполняться условие z = m + n – 1, где z – число занятых клеток; m, n – число строк и столбцов в расчётной таблице.
z = 4 + 2 – 1 = 5, следовательно требование к начальному плану соблюдается.
Суммарная стоимость перевалки грузов в результате реализации плана, составит
E нач = 9×2000 + 8×4000 + 15×6000 + 25×3000 + 21×5000 = 310000 руб.
Для улучшения начального плана воспользуемся методом потенциалов. Система потенциалов строится в соответствии с условием ni = uj + cij, если xij > 0,
где uj – потенциал строки, ni – потенциал столбца.
Присваиваем строке, содержащей заполненную клетку (с наибольшей стоимостью) произвольный потенциал, и далее с учетом приведенного условия рассчитываем потенциалы остальных строк и столбцов.
Таблица 4.3
| Род груза | Потенциалы | Стоимость перевалки 1 т груза по вариантам, руб. | 
| |
| судно – вагон | судно – склад – вагон | |||
 nj
ui nj
ui
| ||||
| Руда | 3 6000 | |||
| Уголь | ||||
| Металл | 2 3000 | |||
| Гравий | ||||
| Пj |
Принимая для третьей строки потенциал u 3 = 5, потенциал второго столбца составит n 2 = 5 + 25 = 30. По известному потенциалу второго столбца, определяем потенциалы остальных строк и первого столбца:
u 1 = 30 – 15 =15; n 1 = 15 + 9 = 24; u 2 = 24 – 8 =16; u 4 = 30 – 21 =9.
Условие II. Для свободных клеток, в которых нет объёмов перевозок, должно выполняться условие 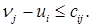
Проверим выполнение условия оптимальности всех свободных клеток:
для клетки 2.2: n 2 – u 2 = 30 – 16 = 14 > 12 – условие не выполняется;
для клетки 3.1: n 1 – u 3 = 24 – 5 = 19 > 15 – условие не выполняется;
для клетки 4.1: n 1 – u 4 = 24 – 9 = 15 > 12 – условие не выполняется.
Выбираем клетку с максимальным нарушением условия оптимальности (клетка 3.1) и строим замкнутый контур. Одна из вершин контура, должна находиться в этой свободной клетке, а остальные вершины в базисных клетках. Контур будет состоять из вершин в клетках: 3.1 – 3.2 – 2.2 – 2.1, нумерация вершин начинается с незанятой клетки.
Далее в таблице уменьшаем объем грузов в четных клетках контура и увеличиваем в нечётных, на наименьшую величину (чтобы не было отрицательных значений). В данном контуре наименьшая величина в четных клетках 2000 т.
Следовательно, объёмы перевалки в нечётных клетках контура (2.2 и 3.1) могут быть увеличены на 2000 т. Для нового плана перевозок в таблице 4.4 рассчитаем потенциалы и проверим на выполнение условия оптимальности.
Таблица 4.4
| Род груза | Потенциалы | Стоимость перевалки 1 т груза по вариантам, руб. | 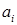 , т , т
| |
| судно – вагон | судно – склад – вагон | |||
 nj
ui nj
ui
| ||||
| Руда | ||||
| Уголь | 2 4000 | |||
| Металл | 3 2000 | 4 1000 | ||
| Гравий | ||||
| Пj |
Проверим свободные клетки 1.1, 2.2 и 4.1 на условие оптимальности:
n 1 – u 1 = 20 – 15 = 5 < 9 – условие выполняется; n 2 – u 2 = 30 – 12 = 18 > 12– условие не выполняется; n 1 – u 4 = 20 – 9 = 11 < 12 – условие выполняется.
Проверка на выполнение условия оптимальности показывает, что нарушение имеется для клетке 2.2
Для устранения нарушений составим новый план в табл. 4.5.
Таблица 4.5
| Род груза | Потенциалы | Стоимость перевалки 1 т груза по вариантам, руб. | 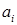 , т , т
| |
| судно – вагон | судно–- склад – вагон | |||
n  j
ui j
ui
| ||||
| Руда | ||||
| Уголь | 3 1000 | |||
| Металл | ||||
| Гравий | 2 5000 | |||
| Пj |
Нарушение имеется в клетке 1.1 и в клетке 1.4 (наибольшее нарушение). Для устранения нарушения выполним итерацию.
Таблица 4.6
| Род груза | Потенциалы | Стоимость перевалки 1 т груза по вариантам, руб. | 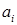 , т , т
| |
| судно – вагон | судно – склад – вагон | |||
n  j
ui j
ui
| ||||
| Руда | ||||
| Уголь | ||||
| Металл | ||||
| Гравий | ||||
| Пj |
Нарушений условия нет, следовательно, план можно принимать за оптимальный.
Анализ полученного плана показывает, что оптимальный вариант перевалки, если:
– по прямому варианту перегружается 3000 т металла и 3000 т гравия;
– через склад 8000 т руды, 4000 т угля и 2000 т гравия.
Расходы на перевалку составят:
E = 15×8000 + 12×4000 + 15×3000 + 12×3000 + 21×2000 = 291000 руб.
Сравнивая с первоначальным планом Eнач = 310000 руб., экономия составляет 310000 – 291000 = 19000 руб.
Контрольные вопросы:
1. Какой метод может служить при составлении начального плана распределения перевалки груза?
2. Показатели оптимального плана распределения перевалки грузов в порту?
В соответствии с федеральным законом «О транспортно-экспедиционной деятельности», экспедиторское обслуживание – это комплекс услуг по организации перевозок грузов любыми видами транспорта и оформлению перевозочных документов, документов для таможенных целей и других документов, необходимых для осуществления перевозок грузов.
При приеме груза экспедитор обязан выдать клиенту экспедиторский документ, а также представить клиенту оригиналы договоров, заключенных экспедитором в соответствии с договором транспортной экспедиции от имени клиента на основании выданной им доверенности. Экспедитор не имеет права заключать от имени клиента договор страхования груза, если это прямо не предусмотрено договором транспортной экспедиции.
Клиент обязан своевременно представить экспедитору полную, точную и достоверную информацию о свойствах груза, об условиях его перевозки и иную информацию, необходимую для исполнения экспедитором обязанностей, предусмотренных договором транспортной экспедиции, и документы, необходимые для осуществления таможенного, санитарного контроля, других видов государственного контроля.
При ТЭО контейнерных перевозок автотранспортом определены основные виды маршрутов движения автомобилей:
- маятниковый маршрут «контейнерный пункт – клиент» с перевозкой контейнеров в обоих направлениях;
- маятниковый маршрут «контейнерный пункт – клиент» с перевозкой контейнеров в одном направлении;
- маятниковый маршрут «контейнерный пункт – клиент» с загруженным плечом в одном направлении и неполно загруженным плечом в другом направлении;
- кольцевой маршрут объезда клиентов, начинающийся и заканчивающийся на контейнерном пункте.
Для оптимизации развоза грузов и контейнеров применяются методы экономико-математического программирования; теории вероятностей и математической статистики; теории графов; логистические методы и др.
Методы экономико-математического программирования, которые используются для решения задач функционирования экономического объекта и поиска оптимальных моделей распределения ресурсов, формализующихся соответствующими целевыми функциями минимума затрат или максимума транспортной продукции. Для решения данных задач рациональной деятельности применяются алгоритмы линейного и нелинейного программирования.
Методы линейного программирования позволяют находить оптимальные решения на основе анализа транспортных потоков. Такие задачи математического программирования сводятся к отысканию значений параметров, обеспечивающих экстремум целевой функции (минимума затрат, максимума продукции) при определенных ограничениях. Данные оптимизационные модели отражают математическую форму экономической задачи и позволяют получить множество решений, удовлетворяющих условию задачи.
В общем виде постановка задачи математического программирования заключается в определении наибольшего или наименьшего значения целевой функции f (x1, x2, ….., xn) при условиях gi (x1, x2, ….., xn)≤ bi; где i = 1, 2, …., m; f, gi – заданные функции; bi – заданные действительные числа.
Задачи математического программирования делятся на задачи линейного и нелинейного программирования:
если f, gi – линейные функции, то данная задача относится к классу линейного программирования;
если хотя бы одна из функций f или gi – нелинейная, то данная задача относится к классу нелинейного программирования.
Постановка транспортной задачи линейного программирования:
некоторый груз Аi, находящийся у m поставщиков (на распределительных контейнерных терминалах) в количестве аi тонн (штук) (i = 1, 2, …., m), необходимо перевезти к n потребителям (заводам, базам) Вj в количестве bj (j = 1, 2, …., n) тонн. Известна стоимость перевозки единицы груза сij от i -поставщика к j -потребителю. Требуется составить такой план перевозок, при котором весь груз вывезен, удовлетворены потребности потребителей и транспортные расходы минимальны.
Для решения задачи принято обозначение хij – количество единиц груза, запланированных к перевозке от i -поставщика к j -потребителю. Стоимость перевозки составит сij∙ хij.
Транспортная задача относится к двухиндексным задачам линейного программирования и выражается двойной суммой
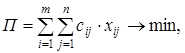 (5.1)
(5.1)
при следующих условиях:
1) все грузы должны быть перевезены 
2) все потребности должны быть удовлетворены 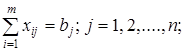
3) запланированное к перевозке от i -поставщика к j -потребителю количество груза хij ≥ 0.
Для составления исходного плана перевозок при решении транспортной задачи методами последовательного улучшения плана применяются: способ северо-западного угла (диагональный), способ наименьшего значения критерия, способ двойного предпочтения, метод аппроксимации Фогеля, случай вырождения, метод потенциалов, сетевые и матричные способы и другие решения.
Частным случаем применения теории вероятностей и математической статистики является выборка результатов по методу Монте-Карло, которым можно решать задачи поиска кратчайших маршрутов развоза местного груза в транспортном узле при экспедиционном обслуживании клиентов (вариант задачи коммивояжера).
Например, вершину 1 транспортной сети (контейнерный терминал) принимают за начальную точку. В «урну» (барабан) закладывают жетоны с номерами от 2 до n (номера грузополучателей). Жетоны перемешивают, вытаскивают по одному и записывают номера: i2, i3, …,in. При этом получается гамильтонов контур, начинающийся и заканчивающийся в пункте развоза груза: 1, i2, i3, …, in, 1. Рассчитывается и запоминается длина полученного контура объезда клиентов. Затем жетоны опять складываются в барабан, перемешиваются и процедура повторяется. Если длина нового контура (маршрута) окажется короче предыдущей, то старый вариант вычеркивается, а новый – запоминается. Если такую процедуру повторять многократно, то можно с высокой степенью вероятности найти достаточно хороший маршрут развоза груза.
По теории графов транспортная задача закрытого типа представляется в виде транспортной сети, пример которой приведен на рис. 5.1. В графе транспортной сети узлами являются КП и грузополучатели, а её рёбрами – автодороги. Каждое ребро имеет «вес» – расстояние перевозки в км.
Для оптимизации прокладки маршрутов автотранспорта граф транспортной сводится в матрицу связей 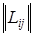 .
.
В исходную матрицу вписываются прямые связи между вершинами в км. Если нет прямой связи в матрицу вписывается «М». Начальная матрица связей транспортной сети изображена в табл. 7.
На втором этапе проверяются связи через другие вершины, обозначенные «М». Сравниваются несколько вариантов доставки и минимальное значение вписывается вместо «М». Матрица связей на втором этапе имеет следующий вид.
Таблица 5.1
Матрица связей транспортной сети 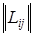
 i j i j
| КП | … | ||||||
| КП | l кп1 | l кп2 | l кп3 | l кп4 | l кп5 | l кп6 | … | |
| l 1-кп | l 1–2 | М | М | М | l 1–6 | … | ||
| l 2-кп | l 2–1 | l 2–3 | М | l 2–5 | l 2–6 | … | ||
| l 3-кп | М | l 3–2 | l 3–4 | l 3–5 | l 3–6 | … | ||
| l 4-кп | М | М | l 4–3 | М | l 4–6 | … | ||
| l 5-кп | М | l 5–2 | l 5–3 | М | М | … | ||
| l 6-кп | l 6–1 | l 6–2 | l 6–3 | l 6–4 | М | |||
| … | … | … | … | … | … | … |

Рис. 5.1 Пример графа транспортной сети
Таблица 5.2
Матрица связей транспортной сети после преобразования
 i j i j
| КП | … | ||||||
| КП | l кп1 | l кп2 | l кп3 | l кп4 | l кп5 | l кп6 | … | |
| l 1-кп | 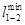
| 
| 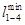
| 
| 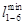
| … | ||
| l 2-кп | 
| 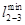
| 
| 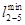
| 
| … | ||
| l 3-кп | 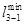
| 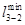
| 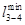
| 
| 
| … | ||
| l 4-кп | 
| 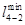
| 
| 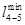
| 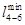
| … | ||
| l 5-кп | 
| 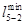
| 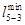
| 
| 
| … | ||
| l 6-кп | 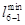
| 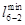
| 
| 
| 
| |||
| … | … | … | … | … | … | … |
Для оптимизации пробега автотранспорта по кольцевому маршруту, объезда всех получателей с однократным посещением составляется Гамильтонов цикл. Длина такого цикла должна быть минимальной, начинаться и заканчиваться на КП. Матрица оптимального маршрута приведена в табл. 5.3.
Таблица 5.3
Оптимальная матрица связей транспортной сети 
 i j i j
| КП | … | ||||||
| КП | 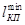
| |||||||
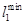
| ||||||||

| ||||||||
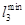
| ||||||||
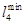
| ||||||||
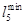
| ||||||||

| ||||||||
| … |
Длина кольцевого маршрута определется суммой 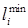 .
.
Для составления кольцевых маршрутов в первом приближении может использоваться один из логистических методов – алгоритм Свира.
Для решения задачи задается положение потребителей контейнеропотока в полярной системе координат (рис. 5.2). Полюс системы – точка «0» размещается в месте дислокации контейнерного терминала. Выбирается начальное положение полярной оси φ = 0. Положение потребителя определяется растоянием от КП и углом φ, который образован полярной осью.
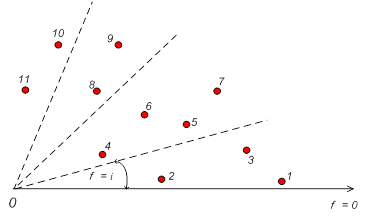
Рис. 5.2 Декомпозиция транспортной сети при составлении маршрутов
развоза контейнеров по методу Свира
По методу Свира полярная ось как щетка вращается против (или по) часовой стрелки, «стирая» при этом с координатного поля изображения потребителей материального потока. Как только сумма заказов «стертых» клиентов достигнет вместимости транспортного средства, фиксируется сектор, обслуживаемый одним кольцевым маршрутом, и намечается путь объезда потребителей. Формирование кольцевых маршрутов завершается при полном обороте «стирающего» луча. В пределах каждого сектора может выполняться частная оптимизация развоза.
|
|
|
|
|
Дата добавления: 2014-11-09; Просмотров: 1011; Нарушение авторских прав?; Мы поможем в написании вашей работы!