
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Психологический и логический способы исследования интеллекта
|
|
|
|
При анализе интеллекта необходимо, считает Пиаже, сочетать психологический и логический планы исследования. В этом утверждении и в его четком осуществлении — одна из важнейших особенностей теории мышления Пиаже.
Хотя уже при написании своих ранних работ Ж. Пиаже были хорошо известны принципы новой логики — математической, или логистики, он, стремясь к «чистоте» психологического анализа, считал, 'что попытки поспешного дедуктивного изложения данных опыта легко приводят к тому, что исследователь оказывается «во власти предвзятых идей, легковесных аналогий, подсказываемых историей наук и психологией первобытных народов, или, что еще более опасно, во власти предубеждений логической системы или системы эпистемологической»39 (разрядка наша. — В. Л. и В. С.). «Классическая логика (т. е. логика учебников) и наивный реализм здравого смысла, — писал он, — два смертельных врага здоровой психологии познания...»40.
Критическое отношение Ж. Пиаже к «логике учебников» представляет собой в значительной степени реакцию против ло-гизации психологии мышления, широко распространенной в XIX в. Сам Пиаже следующим образом характеризует имевшую место в тот период ситуацию. Классическая формальная логика (т. е. доматематическая логика) считала, что возможно раскрыть действительные структуры мыслительных процессов, а классическая философская психология в свою очередь полагала, что законы логики имплицитно присутствуют в умственном функционировании каждого нормального индивида. Между этими двумя дисциплинами в тот период не было оснований для разногласий41.
________________________
39 Ж. Пиаже. Речь и мышление ребенка, стр. 64.
40 Там же.
41 J. Рiаgеt. Logic and psychology. Manchester University Press, 1953, р. 1.
Однако в последующем развитии экспериментальной психологии из нее были исключены логические факторы как «чуждые» для исследуемого в ней предмета. Попытки же сохранить единство психологического и логического исследования, как они имели место, например, у сторонников Вюрцбургской психологической школы, не увенчались успехом. Использование логики в «каузальном объяснении собственно психологических фактов»42 получило название «логицизма» в психологическом исследовании и, начиная с конца XIX в., рассматривалось как одна из важнейших опасностей, которую должен избежать психолог-экспериментатор. «Большинство современных психологов, — пишет Ж. Пиаже, — пытаются объяснить интеллект без какого-либо обращения к логической теории»43.
Такому положению дел способствовали и изменения в теоретическом истолковании логики, происшедшие в конце XIX в. Вместо понимания логики как части психологии, законы которой выводятся из эмпирических фактов интеллектуальной жизни людей («психологизм» в логике), господствующим стало рассмотрение логики как совокупности формальных исчислений, устанавливающих правила преобразования одних языковых форм в другие, которые независимы от эмпирического психологического материала и не имеют отношения к анализу процесса мышления. Пиаже совершенно справедливо отмечает, что «большинство современных логиков не касаются более вопроса о том, имеют ли законы и структуры логики какого-либо рода отношение к психологическим структурам»44. Между психологией мышления и современной формальной логикой образовалась с начала XX в., казалось бы, непреодолимая стена.
Выступая в своих ранних работах за «чистоту» психологического анализа, против внесения элементов логики в психологическое исследование, Ж. Пиаже бесспорно отдавал дань господствующим в тот период воззрениям. Но его позицию, даже в тот период, ни в коем случае нельзя рассматривать как принятие точки зрения абсолютной разделенности психологического и логического исследований. Пиаже боролся против внесения элементарной, «школьной» логики в психологию и против истолкования мышления ребенка с точки зрения логических структур мышления взрослого человека, а не против использования логики в психологии вообще. В своих ранних работах он исходит из того, что мышление взрослого есть логическое мышление, т. е. подчиняющееся совокупности навыков, «применяемых умом при общем ведении операций»45, и свое основное внимание Пиаже обращает на анализ специфических особенностей логики ребенка, не сводимой к логическому мышлению взрослого46.
________________________
42 J. Piaget. Logic and psychology, p. 1.
43 Там же, стр. 2.
44 Там же.
45 Ж. П и а ж е. Речь и мышление ребенка, стр. 97.
46 Там же, стр. 370 — 408.
Таким образом, уже ранние работы Ж. Пиаже характеризовались по сути дела стремлением к единству психологического и логического анализа. Однако реальное осуществление такого единого анализа было дано Пиаже лишь в 30-е годы.
Основная задача, которую решает Ж. Пиаже в своих исследованиях проблем логики, состоит в решении вопроса о том, имеется ли соответствие между логическими структурами и операциональными структурами психологии. В случае положительного решения этого вопроса реальное развитие мыслительных операций получает логическое обоснование,
По мнению Ж. Пиаже, три основные трудности возникают при сопоставлении аксиоматических логических теорий с психологическим описанием реального развития интеллекта: 1) мышление взрослого не формализовано; 2) развертывание аксиоматической логики в определенном отношении противоположно генетическому порядку построения операций (например, при аксиоматическом построении логика классов выводится из логики высказываний, в то время как с генетической точки зрения пропозициональные операции выводятся из логики классов и отношений; 3) аксиоматическая логика имеет атомарный характер (ее основу составляют атомарные элементы) и способ доказательства, используемый в ней, носит по необходимости линейный характер; реальные операции интеллекта, напротив, сорганизованы в некоторые целостные, структурные образования и только в этих рамках они и выступают как операции мышления47.
Аксиоматическое построение логики не является, однако, исходным в самой логике. И исторически, и теоретически ему предшествует некоторое содержательное рассмотрение логических понятий — в виде анализа систем логических операций (алгебра логики). Именно эти операционально-алгебраические структуры могут выступить, по мнению Ж. Пиаже, в качестве посредствующего звена между психологическими и логическими структурами.
Учитывая сказанное, Пиаже считает, что логике и ее отношению к психологии мышления можно дать следующую интерпретацию48.
________________________
47 См. J. Piаgеt. Logic and psychology, p. 24.
48 См. J. Piaget. La psychologie de l'intelligence, p. 37 — 43.
Современная формальная логика при всем ее формализованном и весьма абстрактном характере является в конечном итоге специфическим отражением реально совершающегося мышления. Это означает, что логику можно рассматривать как аксиоматику мышления, а психологию мышления — как соответствующую логике экспериментальную науку. Аксиоматика является гипотетико-дедуктивной наукой, которая старается свести к минимуму апеллирование к опыту и воспроизводит объект с помощью ряда недоказуемых утверждений (аксиом), из которых она выводит все возможные следствия с помощью наперед заданных, строго фиксированных правил. Аксиоматику можно рассматривать как своеобразную «схему» реального объекта. Но именно в силу «схематического» характера всякой аксиоматики она не может ни заменить соответствующую экспериментальную науку, ни считаться лежащей в «основе» последней, так как «схематизм» аксиоматики — это свидетельство ее очевидно ограниченности.
Логика, будучи идеальной моделью мышления, не испытывает никакой нужды в апеллировании к психологическим фактам, так как гипотетико-дедуктивная теория непосредствен» не анализирует факты, а лишь в какой-то крайней точке соприкасается с экспериментальными данными. Однако поскольку определенная связь с фактическими данными все же присуща всякой гипотетико-дедуктивной теории, поскольку всякая аксиоматика является «схемой» некоего реально существующего объекта, постольку между психологией и логикой должно быть некоторое соответствие (хотя между ними никогда не существует параллелизма). Это соответствие логики и психологии имеет место в той мере, в какой психология анализирует конечные положения равновесия, которых достигает развитый интеллект.
Для того чтобы данные современной формальной логики можно было использовать в целях объяснения в психологии, необходимо выделить операционально-алгебраические структуры логики. Решение этой задачи дано в ряде работ Пиаже49.
________________________
49 См. J. Piaget. Classes, relations et nombres. Essai sur les groupements de la logistique et sur la reversibilite de la pensee. Paris, 1942; J. Piaget. Traite de logique. Paris, 1949.
Важнейшую роль в этих исследованиях Ж. Пиаже играет понятие группировки, производное от понятия группы. Под группой в алгебре понимают множество элементов, удовлетворяющих следующим условиям: 1) соединение двух элементов множества дает новый элемент данного множества; 2) каждая операция, применяемая к элементам множества, может быть аннулирована обратной (инверсной) операцией; 3) операции множества ассоциативны, например: (х + х') + у = х + (х' + у); 4) существует один и только один идентичный оператор (0), который, будучи применен к операции, не меняет ее, и который является результатом применения к прямой операции ей инверсной (х + 0 = х; х — х = 0). Группировка получается, если к четырем условиям группы добавить еще пятое условие: 5) наличие тавтологии: х + х = х; у + у = у.
Рассмотрим для примера простую классификацию, где В делится на А и не = А (А'), С — на В и В' и т. д. Схематически простую классификацию можно представить так:
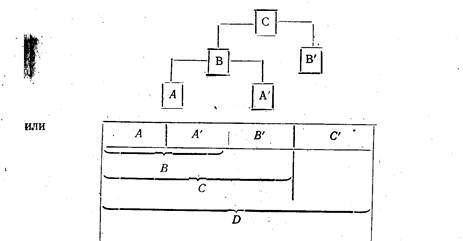
Законы образования простой классификации таковы:
(1) А + А' = В
(2) А + (А' + В') = (А + А') + В'
(3) А + 0 = А
(4) А +(-А) = 0
(5) А + А = А.
Выполнение первых четырех условий показывает, что простая классификация представляет собой группу. Но в ней выполняется еще и пятое условие, которое можно интерпретировать следующим образом: групповая операция «+» означает соединение всех элементов двух множеств, соединенных этой операцией в одно множество, в которое все элементы входят по одному разу (если какой-либо элемент содержится в обоих множествах, то в результирующее множество этот элемент попадает лишь один раз). В силу сказанного понятно, что А + А = А, ибо все элементы второго множества содержатся в первом. Таким образом, простая классификация представляет собой группировку, точнее, одну из элементарных группировок логики классов.
Пиаже устанавливает восемь таких элементарных группировок логики классов и отношений. Каждая из таких группировок имеет точно определенную структуру; часть из этих структур достаточно элементарна (как в приведенном примере с простой классификацией), остальные — более сложны. Для отношений существует группировка (аддитивная группировка асимметричных отношений), изоморфная группировка простой классификации. Охарактеризуем эту группировку.
Пусть А → В есть отношение «В больше А», которое является асимметричным и транзитивным. Будем его записывать так: А 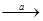 В, где а — величина отличия В от А; соответственно: А
В, где а — величина отличия В от А; соответственно: А 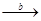 С, В
С, В 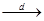 С, C
С, C 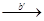 D, C
D, C 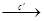 D и т. д.
D и т. д.
Сложение асимметричных отношений образует группировку:
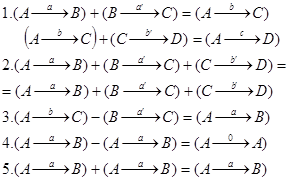
Логические группировки классов и отношений представляют, по мнению Пиаже, определенные структуры, служащие в качестве эталона, к которому «стремятся» реальные операции мышления на определенном уровне их развития (так называемый уровень конкретных операций). Психологически, таким образом, они могут рассматриваться как определение формы равновесия интеллекта. При этом каждое условие группировки получает соответствующее психологическое истолкование: первое условие говорит о возможности координации действий субъекта, второе — утверждает известную свободу направленности действия (условие ассоциативности), третье (наличие обратной операции) — возможность аннулировать результат предшествующего действия (что есть в интеллекте и чего нет, например, в восприятии) и т. д.
Овладение субъектом соответствующими логическими операциями выступает, по Пиаже, критерием его интеллектуального развития. Все восемь группировок логики классов и отношений относятся Пиаже к так называемому конкретно-операциональному уровню развития интеллекта. Над ним надстраивается и из него образуется четвертый уровень — стадия формальных операций, где субъект овладевает логическими связями, имеющими место в логике высказываний.
В связи с этим перед Пиаже встает вопрос о логических структурах этого более высокого уровня развития интеллекта — стадии формальных операций. При исследовании этой проблемы, проведенной, в частности, в «Логическом трактате», Пиаже пришел к следующим выводам50.
1. Для каждой операции исчисления высказываний имеется инверсная операция (N), которая является дополнением по отношению к полному утверждению. Так, для р 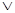 q, нормальная форма которой pq\/pq\/ pq, инверсной будет операция pq; для р
q, нормальная форма которой pq\/pq\/ pq, инверсной будет операция pq; для р 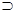 q — pq, и т. д.
q — pq, и т. д.
2. Для каждой операции имеется реципрокная операция (R), т. е. та же самая операция, но производимая над высказываниями инверсных знаков: для p \/ q — р \/ q, для pq — pq и т. д.
3. Для каждой операции имеется коррелятивная операция (С), которая получается путем замены в соответствующей нормальной форме знака V на знак; и обратно. Для p \/ q коррелятивной операцией будет р • q, и обратно.
4. Наконец, если к N, R и С прибавить еще тождественную операцию (/), т. е. операцию, которая оставляет выражение таким же, то множество трансформаций (N, R, С и I) образуют коммукативную группу, задаваемую равенствами
N = (RC (= CR); R = NC (= CN); C ↔ NR (=RN); I = RCN
или таблицей
|
|
|
|
|
Дата добавления: 2014-11-25; Просмотров: 382; Нарушение авторских прав?; Мы поможем в написании вашей работы!