Обратная матрица. Умножение матрицы на скаляр

Пример

Умножение матриц

Умножение матрицы на скаляр

Произведением матрицы на скаляр l является матрица

.

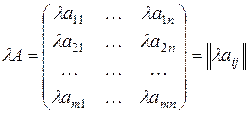Каждый элемент матрицы А умножен на скаляр l.

Произведением матрицы А_mxn на матрицу B_nxr называется новая матрица С_mxr, каждый элемент которой представляет скалярное произведение соответствующей вектор-строки левой матрицы на вектор-столбец правого множителя:

,

где .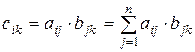

Рассмотрим произведение А_2x4 × B_4x3 = C_2x3 или

,

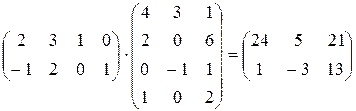где C₁₁ = 14 представляет скалярное произведение вектор-строки (2; 3; 1; 0) на вектор-столбец (4; 2; 0; 1), т.е. 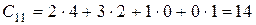и т.д.

Правило. Перемножать можно матрицы только в том случае, когда количество столбцов первой (левой) матрицы равно количеству строк второй (правой) матрицы.

Cвойства операции умножения матрицы.

а) A(B+C)=AB+AC

b) (A+B)C=AC+BC

c) C(AB)=(CA)B

d) .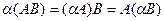

Определителем 2-го порядка называется число, получаемое из элементов матрицы 2-го порядка, представленных в виде квадратной таблицы. Он равен разнице произведений чисел, расположенных по главной и побочной диагоналям:

,

где 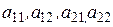- элементы определителя;

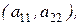- главная диагональ;

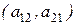- побочная диагональ.

Определителем 3-го порядка называется число, которое можно найти по следующей формуле

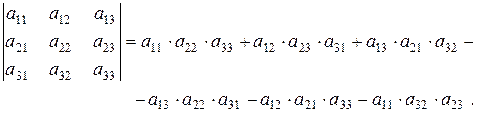
Определитель третьего порядка, также можно найти по теореме Лапласа:

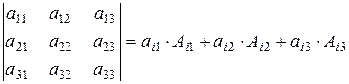
- это разложение по i-й строке. Чтобы вычислить алгебраическое дополнение А_i1 элемента а_i1, вычеркнем мысленно из матрицы, например, вторую (i = 2) строку и первый столбец, на пересечении которых стоит 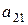. Оставшемуся определителю второго порядка припишем знак (-1)²⁺¹:

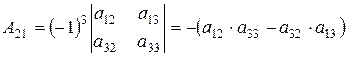
Следующий элемент во второй строке 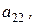а алгебраическое дополнение элемента 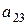будет .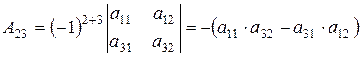

Пусть А - квадратная матрица. Матрица B называется обратной для матрицы А, если произведение этих матриц равно единичной матрице, т.е. АB = BA=E.

Если определитель квадратной матрицы не равен нулю, то эта матрица имеет обратную и притом единственную.

Правило. Для вычисления обратной матрицы необходимо осуществить следующие операции:

1. Вычислить определитель 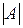исходной матрицы; если он не равен нулю, то обратная матрица существует.

2. Вычислить алгебраические дополнения элементов исходной матрицы: А_11, А_12,..., А_n1,... А_nn.

3. Составить из алгебраических дополнений матрицу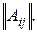

4. Транспонируя полученную матрицу, получить присоединенную .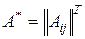

5. Разделив присоединенную матрицу на определитель, получить обратную матрицу ,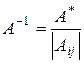

6. Сделать проверку 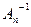∙ 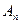=E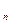

Пример. Вычислить обратную матрицу для .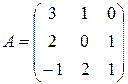

Проводим расчеты по пунктам, описанным выше:

1.

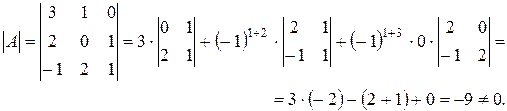
2.

, , ,

, , ,

, , .

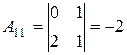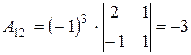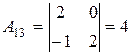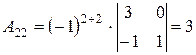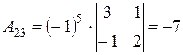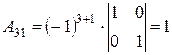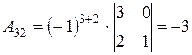3.

.

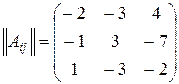4.

.

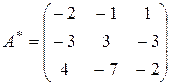5.

=-

.

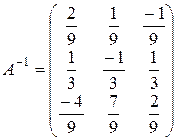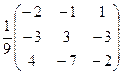
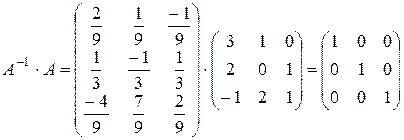Дата добавления: 2014-11-09