
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Контрольная работа №2. Пример. Графически или аналитически отделить корень уравнения и найти этот корень с точностью 0,001 по формуле
|
|
|
|
ТЕМА 10. ПРИБЛИЖЕННОЕ РЕШЕНИЕ УРАВНЕНИЙ
Пример. Графически или аналитически отделить корень уравнения  и найти этот корень с точностью 0,001 по формуле
и найти этот корень с точностью 0,001 по формуле 

Решение. Рассмотрим функцию  . Методом «проб» устанавливаем, что
. Методом «проб» устанавливаем, что  , а
, а  . Значит, на отрезке [0,2] есть корень данного уравнения. При этом
. Значит, на отрезке [0,2] есть корень данного уравнения. При этом  ,а
,а  для всех
для всех  , т.е. сохраняют знак на [0,2]. Значит, можно применить метод Ньютона. Обозначим начальное приближение через x0. Если
, т.е. сохраняют знак на [0,2]. Значит, можно применить метод Ньютона. Обозначим начальное приближение через x0. Если 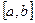 промежуток, в котором изолирован корень функции f(x), то за начальное приближение принимают x=a и x0=b, смотря по тому, в какой из этих точек знак произведения положительно. В данном случае f(2)f”(2)>0, следовательно x0=2.
промежуток, в котором изолирован корень функции f(x), то за начальное приближение принимают x=a и x0=b, смотря по тому, в какой из этих точек знак произведения положительно. В данном случае f(2)f”(2)>0, следовательно x0=2.
Вычисление напишем в виде таблицы
Таблица 9
| №/п | 
| 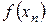
| 
| 
| 
|
| 3,3890 | 6,3890 | 0,5304 | 1,4696 | ||
| 1,4696 | 0,8789 | 3,3485 | 0,2625 | 1,2071 | |
| 1,2071 | 0,1374 | 2,3445 | 0,0586 | 1,1485 | |
| 1,1485 | 0,0048 | 2,1533 | 0,0022 | 1,1463 | |
| 1,1463 | 0,0005 | 2,1468 | 0,0002 | 1,1461 |
Приближенное значение корня найдено с необходимой точностью, и оно равно 1,146.
Задание 1. Вычислить пределы,не пользуясь правилом Лопиталя.
1. a) 

 б)
б)  в)
в) 
2. а) 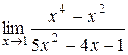 б)
б)  в)
в) 
3. а)  б)
б) 
 в)
в) 
4. а)  б)
б) 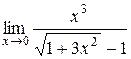 в)
в) 
5. а)  б)
б)  в)
в) 
6. а) 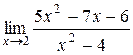 б)
б)  в)
в) 
7. а)  б)
б) 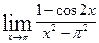 в)
в) 
8. а)  б)
б)  в)
в) 
9. а)  б)
б)  в)
в) 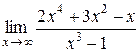
10. а) 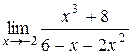 б)
б)  в)
в) 
11. а)  б)
б)  в)
в) 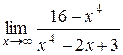
12. а)  б)
б) 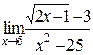 в)
в) 
13. а)  б)
б)  в)
в) 
14. а)  б)
б)  в)
в) 
15. а)  б)
б)  в)
в) 
16. а)  б)
б)  в)
в) 
17. а)  б)
б)  в)
в) 
18. а)  б)
б)  в)
в) 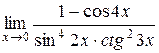
19. а)  б)
б)  в)
в) 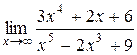
20. а) 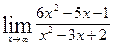 б)
б) 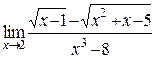 в)
в) 
21. а) 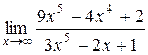 б)
б)  в)
в) 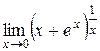
22. а) 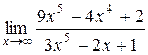 б)
б) 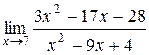 в)
в) 
23. а)  б)
б)  в)
в) 
24. а)  б)
б)  в)
в) 
25. а) 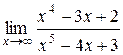 б)
б) 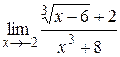 в)
в) 
26. а)  б)
б)  в)
в) 
27. а)  б)
б) 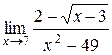 в)
в) 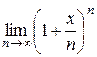
28. а)  б)
б)  в)
в) 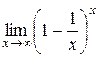
29. а) 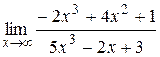 б)
б) 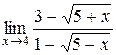 в)
в) 
30. а)  б)
б) 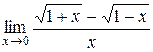 в)
в) 
Задание 2. Задана функция y = f(x). Исследовать эту функцию и построить ee график.
1.y = 
2.y = 
3. x +3 
5. y = 

4. y = 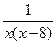
6. y =2x+ctgx
7. y = 
8. y = 
9. y =3 
10. y = 
12. y = 
13. y = 
14. y =ln(x+1)-x
15. y = 
16. y = 
11. y = 
17. y =ln(4-x2)
18. y = 
19. y = 
20. y =2+x-ln(x+3)
21. y = 
22. y =ln 
23. y = 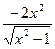
24. y = 
25. y =xlnx
26. y = 
27. y =x-ln(x+1)
28. y =ln 
29. y =xarctgx
30. y =2x+3 
Задание 3.
Найти указанные производные, дифференциалы.
1.
a) 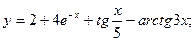

b) 

c) 

d) 

e) 

2.
a) 

b) 

c) 

d) 
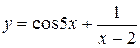
e) 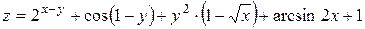

3.
a) 

b) 

c) 

d) 

e) 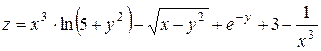

4.
a) 

b) 

c) 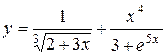

d) 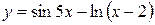

e) 

5.
a) 

b) 

c) 

d) 

e) 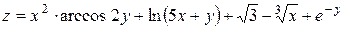

6.
a) 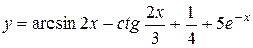

b) 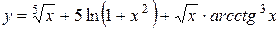

c) 

d) 

e) 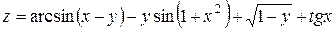

7.
a) 

b) 

c) 

d) 

e) 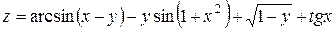

8.
a) 

b) 

c) 

d) 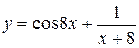

e) 

9.
a) 

b) 

c) 

d) 

e) 

10.
a) 

b) 

c) 

d) 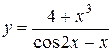

e) 

11.
a) 

b) 

с) 

d) 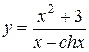

e) 

12.
a) 

b) 

c) 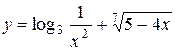

d) 

e) 

13.
a) 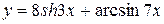

b) 

c) 

d) 

e) 

14.
a) 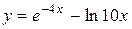

b) 

c) 

d) 

e) 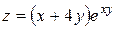

15.
a) 

b) 

c) 

d) 

e) 

16.
a) 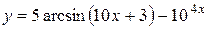

b) 

c) 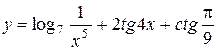

d) 

e) 

17.
a) 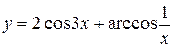

b) 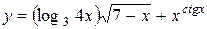

c) 

d) 

e) 

18.
a) 

b) 

c) 

d) 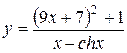

e) 

19.
a) 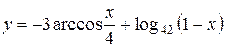

b) 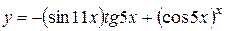

c) 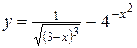

d) 

e) 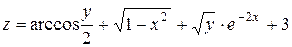

20.
a) 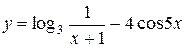

b) 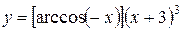

c) 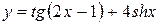

d) 

e) 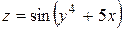

21.
a) 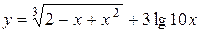

b) 

c) 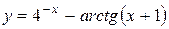

d) 

e) 

22.
a) 

b) 

c) 

d) 

e) 

23.
a) 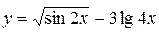

b) 

c) 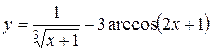

d) 

e) 

24.
a) 

b) 

c) 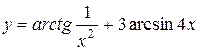

d) 

e) 

25.
a) 

b) 

c) 

d) 

e) 

26.
a) 

b) 

c) 

d) 

e) 

27.
a) 

b) 

c) 

d) 

e) 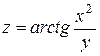

28.
a) 

b) 

c) 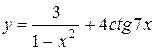

d) 

e) 

29.
a) 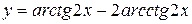

b) 

c) 

d) 

e) 

30.
a) 

b) 

c) 

d) 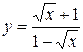

e) 

Задание 4. Определить графически количество действительных корней уравнения f(x) = 0, отделить эти корни и применяя способ Ньютона, найти приближенные значения корней с точностью e = 10-4.
1. 
2. 
3. 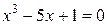
4. 
5. 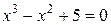
6. 
7. 
8. 
9. 
10. 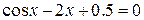
11. 
12. 
13. 
14. 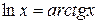
15. 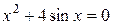
16. 
17. 
18. 
19. 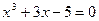
20. 
21. 
22. 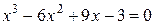
23. 
24. 
25. 
26.х2 = - lnx
27.2х3 - 4х2 + 1 = 0
28.х + sinx - 1 = 0
29.x2 = cosx
30. 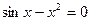
ЛИТЕРАТУРА
1. Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры/ Д.В. Беклемишев.-M.: Наука; 1978.-320с.
2.Пискунов Н.С. Дифференциональное и интегральное исчисление: учебник для втузов: в т. T.1/ Н.С. Пискунов. - М.: Интеграл-Пресс; 1998.-544c.
3.Данко П.Е. Высшая математика в упражнениях и задачах учеб.пособие для втузов/ П.Е. Данко, Попов А.Г., Кожевникова Т.Я.-M.: Высш. шк., 1986, ч. 1.-415c.
|
|
|
|
|
Дата добавления: 2014-11-09; Просмотров: 598; Нарушение авторских прав?; Мы поможем в написании вашей работы!