Исследование функций

Пример 2.

Пример.1

.

Данную функцию можно представить в виде цепочки двух простых функций: ; 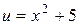.Согласно правилу дифференцирования сложной функции имеем: .

Но , а потому .

.

Очевидно, что 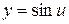и тогда 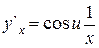,так как , то .

В двух рассмотренных примерах каждая из сложных функций содержала лишь один промежуточный аргумент u и поэтому разлагалась на цепочку из двух простых функций. В более сложных случаях промежуточных аргументов может оказаться больше одного.

В дополнение к примерам, разобранным в тексте учебника, рассмотрим еще следующий пример.

Пример. Исследовать функцию и построить ее график.

1. Область определения данной функции - вся числовая ось, кроме точки

2. Функция не является ни четной, ни нечетной. Действительно, f(-x)= и -f(x).

3. Прямая есть вертикальная асимптота, так как точка есть точка разрыва второго рода.

4.Найдем угловой коэффициент наклонной асимптоты, предполагая, что такая существует: ; .

Находим свободный член b для уравнения асимптоты: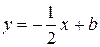

.

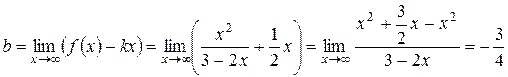Итак, уравнение асимптоты: .

5. Находим критические точки, т.е. точки, в которых первая производная обращается в нуль: .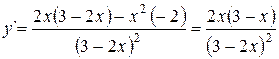

Производная обращается в нуль, если , и .

Подвергая испытанию каждую из этих двух точек, можно узнать, меняется ли знак производной при прохождении аргумента через точки 0 и 3:

а) y¢<0 при x<0 (функция убывает), y¢>0 при x>0 ¢ (функция y возрастает), следовательно, в точке x=0 функция y достигает минимума, причем ;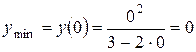

б) при x<3 y¢>0 (возрастает); x>3 y¢<0 (убывает).

Таким образом, в точке x=3 функция достигает максимума, равного .

6. Для уточнения графика функции найдем точки перегиба и установим направление вогнутости (выпуклости) кривой в различных интервалах, для чего обращаемся ко второй производной). Положительный множитель 2, входящий в первую производную, может быть отброшен, поскольку он не влияет на знак второй производной. Имеем

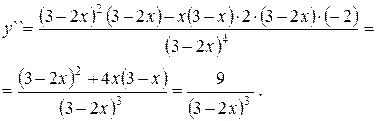
Если , то y²>0 и кривая обращена вогнутостью вверх.

При знаменатель (3- 2х)³ <0 и .

Следовательно, справа от точки разрыва кривая обращена вогнутостью вниз. Точек перегиба нет, y² ни при каком значении из области определения не обращается в нуль. Принимая во внимание выводы всех предыдущих пунктов, строим график функции

Дата добавления: 2014-11-09