Пример 7. Здесь мы имеем «неопределенность типа ( )»

Пример 5.

Найти .

Здесь мы имеем «неопределенность типа ()».

Умножив и разделив эту разность на сопряженное выражение , получим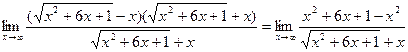

.

Такой предел рассматривался в предыдущем примере. Разделив числитель и знаменатель на x, будем иметь .

Пример 6.

Вычислить

Здесь основание степени 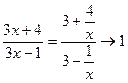при x ,а показатель ; таким образом имеем «неопределенность типа 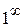». В этом случае следует воспользоваться вторым замечательным пределом:

.

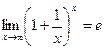Преобразовав выражение, получаем

,

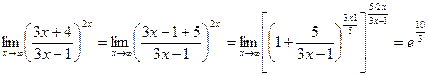так как выражение в квадратных скобках стремится к е, а 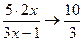при .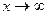

Пусть, например, требуется вычислить .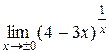

Рассмотрим случай , тогда показатель стремится к , основание к 4, значит искомый предел равен . Если , то показатель ,основание стремится к 4 и искомый предел равен 0. Итак

.

Найти .

Для решения применим предел

Здесь при и числитель и знаменатель стремятся к нулю, получаем «неопределенность типа ». Используя формулу тригонометрии

имеем

Заметим, что cos(15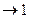x) при x , поэтому

Пример 8.

Найти _.

Известно (следствие теоремы Безу), что если многочлен обращается в нуль при _, то он делится без остатка на , поскольку и числитель и знаменатель рассматриваемой дроби обращается в нуль при х=1 «неопределенность типа », то как и в предыдущей задаче, можно сократить дробь на х-1. Разделив числитель и знаменатель на x-1

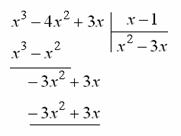
получаем

.

Пример 9.

Найти точки разрыва функции . Изобразить график в окрестности точки разрыва.

Знаменатель 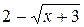, при х=1 обращается в нуль и значит f(x) при x=1 не существует, следовательно, x=1 - точка разрыва функции. Для определения типа разрыва надо найти пределы функции слева и справа при х=1.

При тех же рассуждениях получим .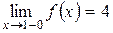

Итак, пределы функции слева и справа при 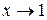равны, но в точке x=1 функция не определена, значит, точка устранимого разрыва. График функции в окрестности точки разрыва выглядит следующим образом:

Такой разрыв называют устранимым разрывом, так как доопределив функцию f(x) надлежащим образом (положив при x=1 f(x) =4) получим непрерывную функцию:

.

ТЕМА 9. ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ

При освоении техники дифференцирования необходимо заучить таблицу производных основных элементарных функций и научиться пользоваться основными правилами дифференцирования. При этом особое внимание следует уделить дифференцированию сложных функций.

Дата добавления: 2014-11-09