Векторное произведение векторов

Ответ:.

2. Проекция вектора на вектор 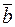вычисляется по формуле:

.

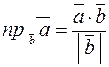Пример. Найти 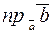, есл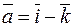и и .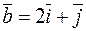

Решение. Координаты векторов , 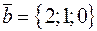. Тогда

.

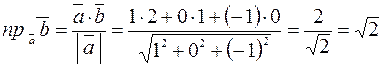Ответ: .

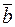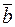Три некомпланарных (непараллельных одной плоскости) вектора , и , взятые в указанном порядке, образуют правую тройку векторов, если из конца третьего вектора поворот от первого вектора ко второму вектору по кротчайшему пути виден против хода часовой стрелки, и левую, если по часовой. (См. рис. 8)

Векторным произведением вектора на вектор 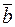называется такой вектор , что:

1) , ;

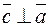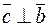2) ;

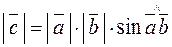3) тройка векторов , , 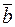и – правая, и обозначается .

Из определения векторного произведения непосредственно вытекают следующие соотношения между ортам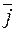и , , и :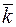

, , .

Поскольку тройки векторов , 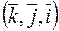и левые, то

, , .

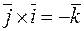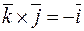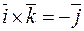Свойства векторного произведения:

1) ;

2) ;

3) , ;

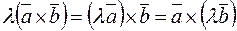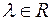4) .

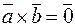
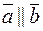Векторное произведение двух векторов и находится по формуле:

.

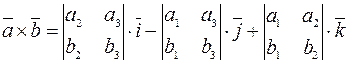Пример. Найти векторное произведение векторов 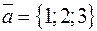и .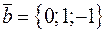

Дата добавления: 2014-11-09