Смешанное произведение векторов

Ответ:.

Решение.

.

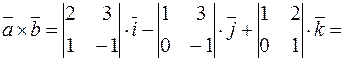
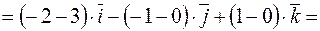
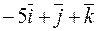Геометрический смысл векторного произведения состоит в том, что площадь параллелограмма, построенного на векторах и 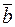(см. рис. 9) равна модулю векторного произведения векторов и 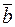, так как:

Следовательно, площадь треугольника, построенного на векторах и 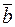(см. рис. 10) равна половине модуля векторного произведения, построенного на векторах и 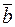, то есть

.

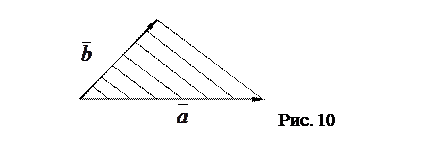
Пример. Найти площадь треугольника, построенного на векторах и .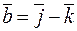

Решение. и 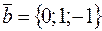. Тогда

;

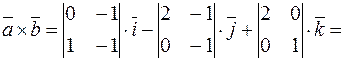
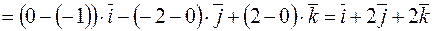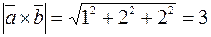, следовательно

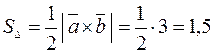(кв. ед.).

Ответ: кв. ед.

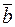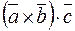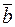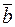
Рассмотрим произведение трех векторов , и , составленное следующим образом: , то есть первые два вектора и умножаются векторно, а их результат скалярно на третий вектор . Такое произведение векторов называется векторно-скалярным или смешанным и обозначается , то есть .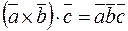

Смешанное произведение трех векторов , 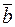и представляет собой число, равное объему параллелепипеда, построенного на этих векторах (см. рис. 11), взятое со знаком «плюс», если эти три вектора образуют правую тройку и со знаком «минус», если они образуют левую тройку векторов.

Свойства смешанного произведения:

1) ;

2) ;

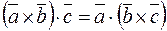3) ; , ;

4) Если 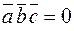, то векторы , 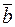и компланарны.

Смешанное произведение трех векторов , 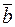и заданных своими координатами, то есть , , вычисляется по формуле:

.

Дата добавления: 2014-11-09