Системы линейных уравнений

МАТЕРИАЛЫ ПО ПОДГОТОВКЕ К СРС

СРС№3. ПРЕДЕЛ И ПРОИЗВОДНАЯ ФУНКЦИИ

МОДУЛЬ 2. Дифференциальное исчисление функции одной переменной. Интегральное исчисление функций одной переменной.

И В ПРОСТРАНСТВЕ

СРС№2. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ

МОДУЛЬ 1. Элементы линейной алгебры и аналитической геометрии. Введение в математический анализ.

СРС№1. ЛИНЕЙНАЯ И ВЕКТОРНАЯ АЛГЕБРА

1. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ

2. ВЕКТОРЫ

1. ПРЯМАЯ НА ПЛОСКОСТИ

2. ПРЯМАЯ И ПЛОСКОСТЬ В ПРОСТРАНСТВЕ

1. ПРЕДЕЛ ФУНКЦИИ

2. ПРОИЗВОДНАЯ

3. ИССЛЕДОВАНИЕ ФУНКЦИИ

СРС№4. НЕОПРЕДЕЛЕННЫЙ и ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

1. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

2. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

3. ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА

4. ФИЗИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО

ИНТЕГРАЛА

5. НЕСОБСТВЕННЫЙ ИНТЕГРАЛ

ЛИТЕРАТУРА

Задания самостоятельной работы следует выполнять в отдельной тетради. На обложке тетради должны быть разборчиво написаны фамилия студента, его инициалы, номер варианта. Номер варианта определяет преподаватель. Если студент выполнил задания не своего варианта, то работа не проверяется и не зачитывается.

Все записи следует делать аккуратно, чертежи выполнять карандашом, с помощью линейки. Решения задач необходимо располагать по порядку их следования в контрольной работе. Текст каждого задания записывать целиком, без сокращений. Решения задач необходимо излагать подробно, объясняя и мотивируя все действия по ходу решения, делая необходимые чертежи.

Защита работы проводится на занятиях СРСП. Если работа не зачтена, то студент должен исправить все отмеченные преподавателем ошибки и недочеты. Выполнить исправления необходимо в этой же тетради.

СРС № 1

Тема: «ЛИНЕЙНАЯ И ВЕКТОРНАЯ АЛГЕБРА»

Решить данную систему уравнений:

1) по формулам Крамера;

2) матричным методом;

3) методом Гаусса.

1. 2x + y +3 z =-9 2. 4x + 3y – 2z = -1 3. 5x - 2y + z = -1

8x+3y + 5z = -13 3x + y + z = 3 2x + y + 2z = 6

2x + 5y- z =-5 x - 2y – 3z = 8 x - 3y – z = -5

4. 3x + 3y + 2z = -1 5. 2x - y + 3z = 1 6. x - 2y + z = 4

2x + y - z = 3 x + 2y + z = 8 2x + y + 3z = 5

x - 2y - 3z = 4 4x - 3y –2z = -1 3x + 4y + z = -2

7. 2x - y + 3z = 3 8. 3x + y – 2z = 1 9. x - 3y - z = 1

x + 2y + z = 2 x - 2y + 3z = 5 2x + y + z = -7

x - 3y +4z = -1 2x + 3y –z = -4 5x- y – 3z = 5

10. 3x + y + 2z = -4 11. 2x + 3y – z = 2 12. 3x - 2y + 2z = 3

x - 2y - z = - 1 x + 2y + 3z = 0 2x + y - z = -5

2x + 3y + 2z = 0 x - y – 2z = 6 5x - y + 3z = 4

13. 5x + 8y – z = 7 14. x + y – z = -2 15. x + 2y + z = 4

x + 2y + 3z = 1 4x-3y + z = 1 3x- 5y + 3z =1

2x - 3y + 2z = 9 2x + y = 5 2x + 7y – z = 8

16. x + y + z = 1 17. x -2y + 3z = 6 18. 4x - 3y + 2z = 9

8x + 3y - 6z = 2 2x+3y - 4z =20 2x + 5y - 3z = 4

-4x - y + 3z = -3 3x- 2y- 5z = 6 5x + 6y - 2z = 18

19. 2x - y + 3z = -7 20. 2x + 2y –3z =0 21. 3x + 2y + 2z = 1

x + 2y - z = 4 x - 2 y +z = 6 2x - 3y – z = 3

3x - 3y - 2z = 1 2x + y + 2z = 5 x - y +3 z = -2

22. x + 2y + z = 1 23. 2x -3y – 5z = 1 24. x - 3y + z = 2

2 x - 3y - 2z = -3 3x + y - 2z = -4 2x + y + 3z = 3

2x + y + z = 2 x - 2y + z = 5 2x - y – 2z = 8

25. x + 5y – z = -1

2x + y - 2z = 7

x - 4y + z = 0

2. «ВЕКТОРЫ»

Даны координаты четырех точек: А, В,С, D и координаты вектора силы .

Требуется найти:

1). момент силы относительно начала координат, если А- точка ее приложения_. Определить направляющие косинусы момента;

2). равнодействующую 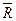сил , где = , = ;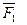

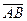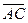3). работу, совершаемую силой 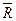при перемещении точки из А в В;

4). угол 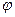между векторам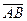и и ;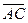

5). площадь треугольника АВС;

6). объем параллелепипеда, построенного на векторах , ;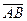

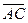1. А = (3,1,-3) 2. А = (-1,2,2) 3. А = (2,1,-4)

B = (-1,-1,1) B = (3,-5,-6) B = (-3,-1,-6)

C = (2,1,-2) C = (2,-6,-4) C = (-2,8,4)

D = (3,2,-3) D = (-8,8,4) D = (-2,8,4)

= (1,-2,-2) = (1,1,-1) = (3,5,-5)

4. А = (7,-3,2) 5. А= (3,8,-3) 6. А = (-1,2,2)

B = (2,2,4) B = (-2,5,2) B = (-2,3,8)

C = (1,-2,-2) C = (1,1,-1) C = (3,5,-5)

D = (3,-3,7) D = (4,-3,-2) D = (-1,5,4)

= (7,4,-3) = (3,2,3) = (-1,-2,1)

7. А= (2,1,-2) 8. А = (1,-1,-1) 9. А = (2,4,-4)

B = (-8,0,1) B = (3,-7,-3) B = (1,-1,-2)

C = (3,2,-3) C = (-8,8,4) C = (-2,8,4)

D = (7,-3,2) D = (6,-3,-2) D = (-9,5,4)

= (1,-2,-9) = (5,3,-7) = (3,5,-5)

10. А = (-1,4,1) 11. А = (-1,3,5) 12. А = (4,-1,2)

B = (2,-6,-2) B = (2,-5,2) B = (-2,1,-1)

C = (7,-2,8) C = (-3,5,3) C = (6,-1,3)

D = (3,2,-3) D = (-8,7,4) D = (-2,8,4)

= (1,-2,-2) = (1,1,-1) = (3,5,-5)

13. А = (0,2,-1) 14. А = (5,1,-4) 15. А = (2,1,3)

B = (7,4,-3) B = (3,2,3) B = (-1,-2,1)

C = (-2,7,2) C = (5,-1,-1) C = (3,2,-3)

D = (2,-3,7) D = (2,-3,-2) D = (-1,2,4)

= (7,4,-3) = (3,2,3) = (-1,-2,1)

16. А = (-2,1,2) 17. А = (-2,1,2) 18. А = (3,-1,4)

B = (3,-2,-3) B = (3,-2,-9) B = (2,-1,5)

C = (1,-3,-1) C = (-3,1,3) C = (-4,2,8)

D = (3,5,-3) D = (-8,8,7) D = (-1,8,4)

= (3,2,-1) = (5,1,-4) = (2,1,3)

19. А= (-1,2,1) 20. А = (1,-2,-1) 21. А = (6,-1,5)

B = (2,-3,7) B = (2,-3,-2) B = (-1,2,4)

C = (4,-5,-4) C = (-4,5,4) C = (2,-3,-6)

D = (9,-3,7) D = (5,-3,-2) D = (-4,5,4)

= (5,2,-1) = (8,1,-4) = (4,1,3)

22. А = (1,5,2) 23. А = (-1,2,-8) 24. А = (-2,1,4)

B = (-1,5,-1) B = (3,6,-9) B =(1,-1,-2)

C = (2,2,6) C = (-2,3,2) C = (3,-2,-6)

D = (6,2,-3) D = (-8,9,4) D = (-2,5,7)

= (3,-2,-3) = (3,-2,-9) = (2,-1,5)

25. А= (-1,2,1) C = (2,-3,-2) = (3,-1,4)

B = (3,-5, 3) D = (9,-2,-3)

СРС №2. «АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ

И В ПРОСТРАНСТВЕ»

1. ПРЯМАЯ НА ПЛОСКОСТИ

Даны координаты вершин треугольника АВС. Найти:

1) длину стороны АВ;

2) уравнения сторон АВ и ВС и их угловые коэффициенты;

3) угол В в радианах с точностью до двух знаков;

4) уравнение высоты СD и ее длину;

5) уравнение медианы АЕ и координаты точки К пересечения этой медианы с высотой СD;

6) уравнение прямой, проходящей через точку К параллельно стороне АВ;

7) координаты точки М, расположенной симметрично точке А относительно прямой СD

1. А (-4; -3), В (6; 12), С (10; 9).

2. А (-5; 7), В (7; -2), С (4; 12).

3. А (-12; -1), В (0; -10), С (7; 15).

4. А (-10; 9,) В (2; 0), С (3; 9).

5. А (0; 2), В (12; -7), С (15; 17).

6. А (-9; 6), В (13; -9), С (8; 10).

7. А (1; 0), В (6; -1), С (4; 12).

8. А (-4; 10), В (2; -4), С (4; 13).

9. А (2; 5), В (8; 1), С (10; 8).

10. А (-1; 4), В (12; -7), С (5; 14).

11. А (-2; 7), В (6; -1), С (3; 9).

12. А(-6;8), В (8; 1), С (13; 15).

13. А (3; 6), В (10; -2), С (17; 13).

14. А (-10; 5), В (8; 3), С (14; 6).

15. А (-4; 12), В (2; -4), С (7; 19).

16. А (-3; 10), В (12; -7), С (13; 6).

17. А (4; 1), В (13; -9), С (5; 14).

18. А (–7; 4), В (6; -1), С (13; 11).

19. А (0; 3), В (13; -9), С (7; 19).

20. А (-5; 9), В (8; 3), С (8; 12).

21. А (4; 3), В (13; -9), С (15; 17).

22. А (-8; -3), В (4; 11), С (7; 15).

23. А (-2; 5), В (6; -1), С (13; 11).

24. А(-6;8), В (8; 1), С (10; 8).

25. А(-4; 9), В (5; 3), С (8; 12).

2. «ПРЯМАЯ И ПЛОСКОСТЬ В ПРОСТРАНСТВЕ»

Даны координаты четырех точек А,В,С, D.

1).написать общее уравнение плоскости, проходящей через три точки А,В,С,

2) преобразовать общее уравнение плоскости к виду в отрезках на осях,

3).определить расстояние от точки D до плоскости

4).найти уравнения прямой АВ и СD,

5).найти угол между прямыми АВ и СD.

1. A (3; 1; 2), B(-1; 6; 5), C(-1; 1; 6), D (0; 4; -1)

2. A (3; 2; 9), B(6; 9; 1), C (1; 4; 4), D (3; 5; 8)

3. A (0; 7; 1), B(4; 1; 5), C (4; 6; 3), D (1; 9; 8)

4. A (2; 5; 4), B(3; 8; 5), C (3; 5; 10), D (5; 8; 2)

5. А(-3; 3; 7), В(-2; 4; 5), С (6; 14; 9) D (8; 5; 8)

6. А(-1; 4; 2), В(1; 5; 0), С(9; 15; 4) D (6; 4; 8)

7. A (6; 1; 4), B(5; 6; 6), C (3; 2; 0), D (4; 2; 6)

8. A (7; 5; 3), B(9; 4; 4), C (4; 5; 7), D (7; 9; 6)

9. A (6; 6; 3), B(5; 4; 7), C (-2; 4; 7), D (7; 3; 0)

10. A (1; 5; 4), B(6; 8; 3), C (4; 9; 9), D (6; 4; 8)

11. A (2; 4; 3), B(7; 6; 3), C (4; 9; 3), D (3; 6; 7)

12. A (9; 5; 5), B(-3; 7;1), C (5; 7; 8), D (6; 9; 2)

13. A (-3; -6; 2), B(1; -2; 0), C (-1; 5; -8), D (-3; -4; 3)

14. A (-4; 2; -1), B(0; 6; -3), C (2; 13; -11), D (-4; 4; 0)

15. A (0; 4; 3), B(4; 8; 1), C (2; 15; -7), D (0; 6; 4)

16. А(-3; 1; 5), В(-1; 2; 3), С (7; 12; 7), D (3; 6; 7)

17. А(-3; -4; 6), В(-3; -3; 4), С (5; 7; 8), D (-4; 4; 0)

18. А(1; -1; 4), В(1; 0; 2), С (11; 10; 6) D (-3; -4; 3)

19. А(-2; -7; 3), В(3; -6; 1), С (8; 4; 5), D (4; -1; 9)

20. A (-2; 0; 2), B(1; 4; -4), C (0; 11; -12), D (-2; 8; -1)

21. A (3; -7; -5), B(-5;- 7; -3), C (0;-8; -7), D (1; -1;- 9)

22. A (9; -4; 0), B(6; -3; 0), C (7; 1; 4), D (6; -6; 6)

23. A (3; -1; -5), B(7; 0; -2), C (6; 4; 2), D (5; -3; 4)

24. A (3; 1; 1), B(9; 2; 1), C (5; 6; 5), D (4; -1; 7)

25. A (-2; 1; -2), B(8; 3; -2), C (1; 7; 2), D (0; 0; 4)

Дата добавления: 2014-11-09