Базис и координаты вектора

Определение Линейной комбинацией векторов а_1, а₂,…,а_n называется выражение вида: k₁ a₁ + k₂ a₂ +…+ k_n a_n, (5.1)

где k_i – числа.

Определение Векторы а_1, а₂,…,а_n называются линейно зависимыми, если найдутся такие числа k₁, k₂,…, k_n, не все равные нулю, что соответствующая линейная комбинация векторов равна нулю, т.е. k₁ a₁ + k₂ a₂ +…+ k_n a_n = 0. (5.2)

Если же равенство (5.2) возможно только при всех k _i = 0, векторы называются линейно независимыми.

Замечание 1. Если система векторов содержит нулевой вектор, то она линейно зависима.

Замечание 2. Если среди n векторов какие-либо (n -1) линейно зависимы, то и все n векторов линейно зависимы.

Замечание 3. Необходимым и достаточным условием линейной зависимости двух векторов является их коллинеарность.

Определение Векторы называются компланарными, если они лежат либо в одной плоскости, либо в параллельных плоскостях.

Замечание 4. Необходимым и достаточным условием линейной зависимости трех векторов является их компланарность.

Замечание 5. Любые четыре вектора в трехмерном пространстве линейно зависимы.

Определение Два линейно независимых вектора на плоскости (или три линейно независимых вектора в пространстве) образуют базис, если любой вектор плоскости (пространства) может быть представлен в виде их линейной комбинации. Числовые коэффициенты этой линейной комбинации называются координатами данного вектора в рассматриваемом базисе:

если a, b, c – базис и d = k a + m b + p c, то числа k, m, p есть координаты вектора d в базисе a, b, c.

Свойства базиса:

1. Любые два неколлинеарных вектора образуют базис на плоскости, а любые три некомпланарных вектора – базис в пространстве.

2. Разложение данного вектора по данному базису единственно, т.е. его координаты в данном базисе определяются единственным образом.

3. При сложении двух векторов их координаты относительно любого базиса складываются.

4. При умножении вектора на число все его координаты умножаются на это число.

Определение Проекцией вектора АВ на ось u называется длина направленного отрезка А^/В^/ оси u, где А^/ и В^/ - основания перпендикуляров, опущенных из точек А и В на ось u.

Обозначение: пр_u а.

Свойства проекции:

1. Пр_u a = | a | cosφ, где φ – угол между а и осью u.

2. При сложении двух векторов их проекции на любую ось складываются.

3. При умножении вектора на число его проекция на любую ось умножается на это число.

2. Декартова система координат. Скалярное произведение векторов.

Зафиксируем в пространстве точку О и рассмотрим произвольную точку М. Вектор 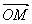назовем радиус- вектором точки М. Если в пространстве задать некоторый базис, то точке М можно сопоставить некоторую тройку чисел – компоненты ее радиус- вектора. Определение. Декартовой системой координат в пространстве называется совокупность точки и базиса. Точка называется началом координат. Прямые, проходящие через начало координат называются осями координат. 1-я ось – ось абсцисс 2-я ось – ось ординат 3-я ось – ось аппликат Чтобы найти компоненты вектора нужно из координат его конца вычесть координаты начала. Если заданы точки А(x₁, y₁, z₁), B(x₂, y₂, z₂), то 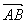= (x₂ – x₁, y₂ – y₁, z₂ – z₁).

Определение. Базис называется ортонормированным, если его векторы попарно ортогональны и равны единице.

Определение. Декартова система координат, базис которой ортонормирован называется декартовой прямоугольной системой координат.

Рассмотрим декартову систему координат, базис которой образуют в пространстве три попарно ортогональных единичных вектора i, j, k. Тогда любой вектор d может быть представлен в виде их линейной комбинации:

d = X i + Y j +Z k.

Определение Числа X, Y, Z называются декартовыми координатами вектора d.

Замечание. Декартовы координаты вектора равны его проекциям на оси Ох, Оу и Оz декартовой системы координат.

Определение Косинусы углов, образованных вектором о осями декартовой системы координат, называются его направляющими косинусами.

Свойства направляющих косинусов:

1. X = | d | cos α, Y = | d | cos β, Z = | d | cosγ.

2. , , .

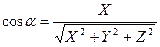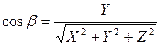3. cos²α + cos²β + cos²γ = 1.

Определение Скалярным произведением двух векторов называется произведение их модулей на косинус угла между ними:

ab = | a || b | cosφ.

Обозначения скалярного произведения: ab, ( ab ), a·b.

Свойства скалярного произведения:

1. ab = | a | пр_а b.

Доказательство. По свойству проекции пр_а b = | b | cos φ, следовательно, ab = | a | пр_а b.

2. ab = 0 a 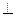b. 3. ab = ba.

4. (k a) b = k(ab). 5. (a + b ) c = ac + bc.

6. a ² = aa = | a |², где а ² называется скалярным квадратом вектора а.

7. Если векторы а и b определены своими декартовыми координатами

a = {X₁, Y₁, Z₁}, b = {X₂, Y₂, Z₂

то ab = X₁X₂ + Y₁Y₂ + Z₁Z₂.

8. cosφ = .

3. Будем называть три вектора а,b,c, для которых определен порядок следования, тройкой (или упорядоченной тройкой) векторов.

Определение Тройка некомпланарных векторов abc называется правой (левой), если после приведения к общему началу вектор с располагается по ту сторону от плоскости, определяемой векторами а и b, откуда кратчайший поворот от а к b кажется совершающимся против часовой стрелки (по часовой стрелке).

с с

b a

Дата добавления: 2014-11-09