Связь цилиндрической и декартовой прямоугольной системами координат

A) Аналогично полярной системе координат на плоскости можно записать соотношения, связывающие между собой различные системы координат в пространстве. Для цилиндрической и декартовой прямоугольной систем эти соотношения имеют вид:

B) h = z; x = rcosq; y = rsinq; cosq = ; sinq = .

// С вязь сферической системы координат с декартовой прямоугольной.

В случае сферической системы координат соотношения имеют вид:

Контрольные вопросы:

1. Поверхности второго порядка.

2. Системы координат

Литература: [3, с. 161,170 ],[8, с.149,175]

Лекция №7 Тема: Переменная величина Предел переменной величины Функция. Предел функции. Основные теоремы о пределах

Цель: Дать понятия переменной величины, предела, функции. Рассмотреть основные теоремы о пределах.

План:

1. Переменная величина Предел переменной величины

2. Функция. Предел функции.

3. Основные теоремы о пределах

1. Переменной величиной называется величина, которая принимает различные числовые значения. Величина, числовые значения которой не меняются, называется постоянной. Переменные величины будем обозначать буквами x, y, z,…, постоянные – a, b, c,…

числовая последовательность – это переменная величина, последовательные значения которой могут быть перенумерованы. Числовую последовательность будем обозначать . Например, числовую последовательность образуют следующие величины:

1. ,

2. ,

3. , где а, d – постоянные числа.

Окрестностью точки x₀ называется произвольный интервал (a, b), содержащий эту точку внутри себя. Часто рассматривается окрестность точки x₀, для которой x₀ является серединой, тогда x₀ называется центром окрестности, а величина (b – a)/2 – радиусом окрестности.

Число a называется пределом последовательности x = { x_n }, если для произвольного заранее заданного сколь угодно малого положительного числа ε найдется такое натуральное число N, что при всех n>N выполняется неравенство |x_n - a| < ε.

Если число a есть предел последовательности x = { x_n }, то говорят, что x_n стремится к a, и пишут .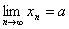

Итак, выясним, что же означает геометрически понятие предела числовой последовательности. Для этого запишем последнее неравенство из определения в виде

Это неравенство означает, что все элементы последовательности с номерами n>N должны лежать в интервале (a – ε; a + ε).

Следовательно, постоянное число a есть предел числовой последовательности { x_n }, если для любой малой окрестности с центром в точке a радиуса ε (ε – окрестности точки a) найдется такой элемент последовательности с номером N, что все последующие элементыс номерами n>N будут находиться внутри этой окрестности.

2. Если каждому значению переменной x, принадлежащему некоторой области, соответствует одно определенное значение другой переменной y, то y называется функцией переменной х. Символически будем записывать y=f(x). При этом переменная x называется независимой переменной или аргументом.

Запись y=C, где C – постоянная, обозначает функцию, значение которой при любом значении x одно и то же и равно C.

Множество значений x, для которых можно определить значения функции y по правилу f(x), называется областью определения функции.

Элементарной функцией называется функция, которая может быть задана основными элементарными функциями и постоянными при помощи конечного числа операций сложения, вычитания, умножения, деления и взятия функции от функции.

К основным элементарным функциям относятся все функции, изучаемые в школьном курсе математики:

Дата добавления: 2014-11-09