Примеры

B)

2. Односторонние пределы

До сих пор мы рассматривали определение предела функции, когда x→a произвольным образом, т.е. предел функции не зависел от того, как располагалось x по отношению к a, слева или справа от a. Однако, довольно часто можно встретить функции, которые не имеют предела при этом условии, но они имеют предел, если x→a, оставаясь с одной стороны от а, слева или справа Поэтому вводят понятия односторонних пределов.

Если f(x) стремится к пределу b при x стремящемся к некоторому числу a так, что x принимает только значения, меньшие a, то пишут и называют bпределом функции f(x) в точке a слева.

Аналогично, если x→a и принимает значения большие a, то пишут 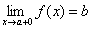и называют b пределом функции в точке а справа. Т.е. число b называется пределом функции y=f(x) при x→a справа, если каково бы ни было положительное число ε, найдется такое число δ (большее а), что для всех 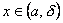выполняется неравенство .

Заметим, что если пределы слева и справа в точке a для функции f(x) не совпадают, то функция не имеет предела (двустороннего) в точке а.

1. 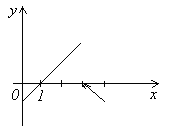Рассмотрим функцию y=f(x), определенную на отрезке [0,1] следующим образом

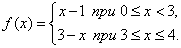Найдем пределы функции f(x) при x→ 3. Очевидно, , а .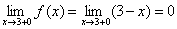

2.

3. .

4. .

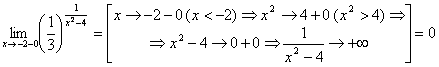пусть имеем функцию y = f(x).

Функция y = f(x) называется непрерывной в точке x₀, если она определена в этой точке и в некоторой окрестности содержащей x₀ и

.

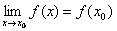(1)

Таким образом, можно сказать, что функция непрерывна в точке x₀, если выполнены 3 условия:

1. она определена в точке x₀ и в некоторой её окрестности;

2. имеет предел при x → x₀;

3. этот предел равен значению функции в точке x₀.

Формулу (1) можно записать в виде 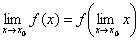, т.к. . Это означает, что для того, чтобы найти предел непрерывной функции при x → x₀, достаточно в выражение функции подставить вместо аргумента x его значение x₀.

Пример: Докажем, что функция y = 3 x ² непрерывна в произвольной точке x₀. Для этого найдем .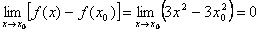

Если функция y=f(x) непрерывна в каждой точке некоторого интервала (a; b), где a < b, то говорят, что функция непрерывна на этом интервале.

Непрерывные функции обладают следующими свойствами.

Теорема 1. Если функции f(x) и g(x) непрерывны в точке x₀, то их сумма φ(x) = f(x) + g(x) также есть непрерывная функция в точке x₀.

Доказательство. Так как функции f(x) и g(x) непрерывны в точке x₀, то исходя из определения можно написать . Тогда на основании свойств пределов будем иметь

.

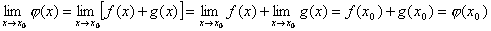Эта теорема справедлива для любого конечного числа слагаемых.

Следующие две теоремы докажите самостоятельно аналогично теореме 1.

Теорема 2. Произведение двух непрерывных функций есть функция непрерывная.

Теорема 3. Частное двух непрерывных функций есть функция непрерывная, если знаменатель в рассматриваемой точке не обращается в нуль.

Если функцию можно представить в виде y = f(u), где u = φ(x), т.е. если функция зависит от переменной через промежуточный аргумент u, то называется сложной функцией переменной x.

Примеры:

1. y = sin x³. Здесь u = x³, y = sin u.

2. y = e^{tg x}, u = tg x, y = e^u.

Таким образом, под термином сложная функция следует понимать не какое – либо очень сложное выражение, а функцию, которая зависит от аргумента x через несколько промежуточных функций.

Справедлива следующая теорема.

Теорема 4. Если функция u = φ(x) непрерывна в точке x₀ и принимает в этой точке значение u₀ = φ(x₀), а функция f(u) непрерывна в точке u₀, то сложная функция y = f(φ(x)) непрерывна в точке x₀.

Используя эти теоремы можно доказать следующий результат.

Теорема 5. Всякая элементарная функция непрерывна в каждой точке, в которой она определена.

Заметим, что если функция y = f(x) непрерывна в точке x₀ и её значение в этой точке отлично от 0, f(x₀) ≠ 0, то значения функции f(x) в некоторой окрестности точки x₀ имеют тот же знак, что и f(x₀), т.е. если f(x₀) > 0, то найдётся такое δ > 0, что на интервале(x₀ – δ; x₀+ δ) f(x) > 0 (в этой окрестности значения функции f(x) очень мало отличаются от своего предела).

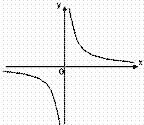Если рассмотреть график функции 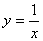в окрестности точки x = 0, то ясно видно, что он как бы “разрывается” на отдельные кривые.

3. Точка называется точкой разрыва функции y = f(x), если она принадлежит области определения функции или её границе и не является точкой непрерывности.

В этом случае говорят, что при x= x₀ функция разрывна. Это может произойти, если в точке x₀ функция не определена или не существует предел 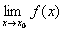, или если предел существует, но .

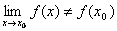Примеры.

1. Рассмотрим функцию:

Эта функция определена во всех точках отрезка [0, 4] и её значение при x = 3 равно 0. Однако, в точке x = 3 функция имеет разрыв, т.к. она не имеет предела при x = 3:

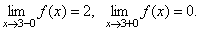
Следует отметить, что f(x) непрерывна во всех остальных точках отрезка [0, 4]. При этом в точке x = 0 она непрерывна справа, а в точке x = 4 – слева, т.к.

.

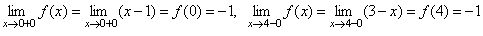2. 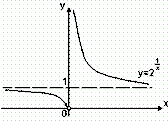Как уже отмечалось, функция 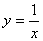разрывна при x = 0. Действительно, при x = 0 функция не определена: .

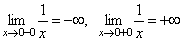3. Функция разрывна при x = 0. Действительно, 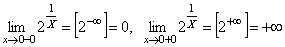. При x = 0 функция не определена.

4. Функция 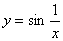определена для всех значений x, кроме x = 0. В этой точке она имеет разрыв, т.к. предел не существует (рисунок см. в лекции 1).

Точки разрыва функции можно разбить на два типа.

Точка разрыва x₀ функции f(x) называется точкой разрыва первого рода, если существуют оба односторонних конечных предела 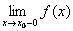и , но они не равны между собой или не равны значению функции в точке x₀, т.е. f(x₀). Точка разрыва, не являющаяся точкой разрыва первого рода, называется точкой разрыва второго рода.

Примеры: В первом примере точка х= 3 является точкой разрыва первого рода. В примерах 2 – 4 все точки разрыва являются точками разрыва второго рода.

5. Для функции, изображённой на рисунке точка x = 2 является точкой разрыва первого рода.

6. Функция 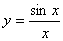не определена в точке x = 0. Эта точка является точкой разрыва 1-го рода, т.к. в ней существуют пределы справа и слева.

Функцию y = f(x) называют непрерывной на отрезке [ a, b ], если она непрерывна во всех внутренних точках этого отрезка, а на его концах, т.е. в точках a и b, непрерывна соответственно справа и слева.

Теорема Функция, непрерывная на отрезке [ a, b ], хотя бы в одной точке этого отрезка принимает наибольшее значение и хотя бы в одной – наименьшее.

Теорема утверждает, что если функция y = f(x) непрерывна на отрезке [ a, b ], то найдётся хотя бы одна точка x₁ Î [ a, b ] такая, что значение функции f(x) в этой точке будет самым большим из всех ее значений на этом отрезке: f(x₁) ≥ f(x). Аналогично найдётся такая точка x₂, в которой значение функции будет самым маленьким из всех значений на отрезке: f(x₁) ≤ f(x).

Ясно, что таких точек может быть и несколько, например, на рисунке показано, что функция f(x) принимает наименьшее значение в двух точках x₂ и x ₂'.

Следствие. Если функция f(x) непрерывна на [ a, b ], то она ограничена на этом отрезке.

Теорема Пусть функция y = f(x) непрерывна на отрезке [ a, b ] и на концах этого отрезка принимает значения разных знаков, тогда внутри отрезка [a, b] найдется, по крайней мере, одна точка x = C, в которой функция обращается в ноль: f(C) = 0, где a < C< b

Эта теорема имеет простой геометрический смысл: если точки графика непрерывной функции y = f(x), соответствующие концам отрезка [ a, b ] лежат по разные стороны от оси Ox, то этот график хотя бы в одной точке отрезка пересекает ось Ox. Разрывные функции этим свойством могут не обладать.

Эта теорема допускает следующее обобщение.

Теорема (теорема о промежуточных значениях). Пусть функция y = f(x) непрерывна на отрезке [ a, b ] и f(a) = A, f(b) = B. Тогда для любого числа C, заключённого между A и B, найдётся внутри этого отрезка такая точка C Î [ a, b ], что f(c) = C.

Следствие. Если функция y = f(x) непрерывна на некотором интервале и принимает наибольшее и наименьшее значения, то на этом интервале она принимает, по крайней мере, один раз любое значение, заключённое между её наименьшим и наибольшим значениями.

Контрольные вопросы:

1. Первый замечательный предел

2 .Второй замечательный предел.

3. Типы неопределенностей.

4. Непрерывность функции в точке.

5. Свойства непрерывных функций.

6. Точки разрыва функции.

Литература: [3, с. 45,50 ],[8, с.30,45]

Лекция №9 Тема: Производная, ее геометрический и механический смысл. Правила дифференцирования. Дифференцирование основных элементарных функций. Производная обратной функции.Таблица производных. Дифференцирование сложной, гиберболических функций.

Цель: Ввести понятие производной.Рассмотреть геометрический и физический смысл производной, основные правила дифференцирования,таблицу производных

План:

1. Производная, ее геометрический и механический смысл. Правила дифференцирования

2. Дифференцирование основных элементарных функций. Производная обратной функции.Таблица производных.

3. Дифференцирование сложной, гиберболических функций.

1. Пусть имеем некоторую функцию y=f(x), определенную на некотором промежутке. Для каждого значения аргумента x из этого промежутка функция y=f(x) имеет определенное значение.

Рассмотрим два значения аргумента: исходное x ₀ и новое x. Разность x– x ₀ называется приращением аргумента x в точке x ₀ и обозначается Δx. Таким образом, Δx = x – x ₀ (приращение аргумента может быть как положительным, так и отрицательным). Из этого равенства следует, что x=x ₀ +Δx, т.е. первоначальное значение переменной получило некоторое приращение. Тогда, если в точке x ₀ значение функции было f(x ₀ ), то в новой точке x функция будет принимать значение f(x) = f(x ₀ +Δx).

Разность y – y ₀ = f(x) – f(x ₀ ) называется приращением функции y = f(x) в точке x ₀ и обозначается символом Δy. Таким образом,

Δy = f(x) – f(x 0 ) = f(x 0 +Δx) - f(x 0 ).

(1)

Составим отношение приращения функции к приращению аргумента

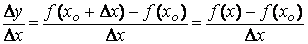
Найдем предел этого отношения при Δx →0. Если этот предел существует, то его называют производной данной функции f(x) в точке x ₀ и обозначают f '(x ₀). Итак,

.

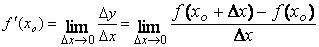Производной данной функции y = f(x) в точке x ₀ называется предел отношения приращения функции Δ y к приращению аргумента Δ x, когда последнее произвольным образом стремится к нулю.

Производная обозначается символами f ' (x),y ', 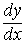. Конкретное значение производной при x = a обозначается f '(a) или y ' |_x=a.

Операция нахождения производной от функции f(x) называется дифференцированием этой функции.

Дата добавления: 2014-11-09