Примеры. 1. Рассмотрим функцию y=|x|.Эта функция непрерывна в точке x = 0, т.к

1. Рассмотрим функцию y=|x|. Эта функция непрерывна в точке x = 0, т.к. 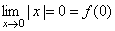.она не имеет производной в этой точке.

Правила дифференцирования

Пусть u=u(x),v=v(x) – две дифференцируемые функции от переменной x.

1.

2. .

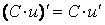3. 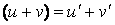(справедлива для любого конечного числа слагаемых).

4. .

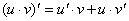5. .

а) .

б) .

C) 2. Производные элементарных функций.

D) y = xⁿ. Если n – целое положительное число, то, используя формулу бинома Ньютона:

(a + b)ⁿ = a ⁿ+ n·a ^n-1· b + 1/2∙ n(n – 1)a ^n-2∙ b ²+ 1/(2∙3)∙ n(n – 1)(n – 2)a^n-3b³+…+ bⁿ,

можно доказать, что

Итак, если x получает приращение Δ x, то f(x +Δ x) = (x + Δ x)ⁿ, и, следовательно,

Δ y =(x +Δ x) ⁿ – xⁿ = n·x^n-1 ·Δ x + 1/2·n·(n– 1 )·x^n-2 ·Δ x² +…+Δ xⁿ.

Заметим, что в каждом из пропущенных слагаемых есть множитель Δ x в степени выше 3.

Найдем предел

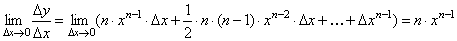
Мы доказали эту формулу для n Î N. Далее увидим, что она справедлива и при любом n Î R.

1. y = sin x. Вновь воспользуемся определением производной.

Так как, f(x +Δ x)= sin(x +Δ x), то

Таким образом,

2. Аналогично можно показать, что

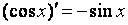
3. Рассмотрим функцию y = ln x.

Имеем f (x +Δ x)=ln(x +Δ x). Поэтому

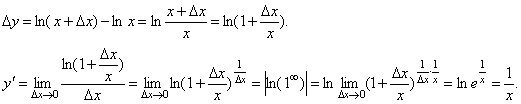
Итак,

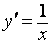
4. Используя свойства логарифма можно показать, что

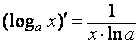
3. Производная обратной функции

Рассмотрим функцию y= x³. Будем рассматривать равенство y = x³ как уравнение относительно x. Это уравнение для каждого значения у определяет единственное значение x: 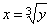. Геометрически это значит, что всякая прямая параллельная оси Ox пересекает график функции y= x³ только в одной точке. Поэтому мы можем рассматривать x как функцию от y. Функция 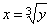называется обратной по отношению к функции y= x³.

Функция y = f(x) называется возрастающей на некотором отрезке, если большему значению аргумента x из этого отрезка соответствует большее значение функции, т.е. если x ₂> x ₁, то f(x ₂ ) > f(x ₁ ).

Аналогично функция называется убывающей, если меньшему значению аргумента соответствует большее значение функции, т.е. если х ₂ < х ₁, то f(x ₂ ) > f(х ₁ ).

Итак, пусть дана возрастающая или убывающая функция y= f(x), определенная на некотором отрезке [ a; b ]. Для определенности будем рассматривать возрастающую функцию (для убывающей все аналогично).

Рассмотрим два различных значения х ₁ и х ₂. Пусть y ₁ =f(x ₁ ), y ₂ =f(x ₂ ). Из определения возрастающей функции следует, что если x ₁< x ₂, то у ₁< у ₂. Следовательно, двум различным значениям х ₁ и х ₂ соответствуют два различных значения функции у ₁ и у ₂. Справедливо и обратное, т.е. если у ₁< у ₂, то из определения возрастающей функции следует, что x ₁< x ₂. Т.е. вновь двум различным значениям у ₁ и у ₂ соответствуют два различных значения x ₁ и x ₂. Т.о., между значениями x и соответствующими им значениями y устанавливается взаимно однозначное соответствие, т.е. уравнение y=f(x) для каждого y (взятого из области значений функции y=f(x)) определяет единственное значение x, и можно сказать, что x есть некоторая функция аргумента y: x= g(у). Эта функция называется обратной для функции y=f(x). Очевидно, что и функция y=f(x) является обратной для функции x=g(у).

Заметим, что обратная функция x=g(y) находится путем решения уравнения y=f(x) относительно х.

Пример. Пусть дана функция y = e^x. Эта функция возрастает при –∞ < x <+∞. Она имеет обратную функцию x = ln y. Область определения обратной функции 0 < y < + ∞

Теорема. Если для функции y=f(x) существует обратная функция x=g(y), которая в некоторой точке у ₀ имеет производную g '(v₀), отличную от нуля, то в соответствующей точке x₀ = g (x₀) функция y=f(x) имеет производную f '(x₀), равную , т.е. справедлива формула .

Дата добавления: 2014-11-09