Порядок выполнения самостоятельной работы 3 страница

Треугольники, из которых состоит тетраэдр, называются гранями, их стороны рёбрами, а вершины – вершинами тетраэдра.

Тетраэдр имеет 4 грани, 6 рёбер, 4 вершины. Два ребра тетраэдра, не имеющие общих вершин, называются противоположными. Иногда выделяют одну из граней тетраэдра и называют её основанием, а три другие – боковыми гранями.

Тетраэдр изображают в виде выпуклого четырёхугольника с диагоналями.

Мы должны различать правильный тетраэдр и правильную треугольную пирамиду. В правильной треугольной пирамиде боковые рёбра равны друг другу, но они могут быть не равны рёбрам основания пирамиды.

2. Практические рекомендации к лабораторной работе.

.

DO – высота тетраэдра.

Приложение №13

Тема:

8.2 Тела вращения и поверхности

Цель: закрепление знаний по теме «Многогранники»

Оснащение: данные методические указания, рекомендуемая литература.

Задания. Провести лабораторное наблюдение и экспериментирование по теме: «Объем тел вращения».

Порядок выполнения задания

1 вариант. Название фигуры – цилиндр.

2 вариант. Название фигуры – конус.

Порядок выполнения работы.

1. Постройте указанную геометрическую фигуру в своей тетради;

2. Обозначьте главные элементы данной фигуры буквами;

3. Выпишите формулы, по которым вычисляется объем данной фигуры;

4. Измерьте по чертежу элементы, входящие в формулы, выпишите их отдельно;

5. Данные измерения подставьте в формулы;

6. Выполните все вычисления в см, если нужно ответ округлите до десятых;

7. Запишите ответ.

1 вариант. Модель тела вращения – конус.

2 вариант. Модель тела вращения – цилиндр.

Порядок выполнения работы.

1. Описать коротко свойства фигуры по модели;

2. Выписать формулу вычисления объёма фигуры и площади основания;

3. Измерить нужные элементы по модели, записать их в тетрадь;

4. Подставить данные в формулы;

5. Вычислить объём фигуры и площадь основания.

Моделью может служить предмет из жизни: стакан, бокал, воронка, колпак, … др.

Вопросы для самопроверки и проверки.

1. Дайте определение тел вращения.

2. Какие фигуры относятся к телам вращения;

3. Перечислите свойства конуса, усечённого конуса;

4. Перечислите свойства цилиндра;

5. Перечислите сечения конуса, цилиндра;

6. Выпишите формулы для вычисления объёмов.

Методические указания по выполнению лабораторного наблюдения и экспериментирования.

1. Теоретические материалы.

Тело, ограниченное цилиндрической поверхностью и двумя кругами с границей L и L₁ называется цилиндром. Цилиндрическая поверхность называется боковой поверхностью цилиндра, а круги основаниями цилиндра.

Образующие цилиндрической поверхности называются образующими цилиндра, прямая ОО₁ – осью цилиндра.

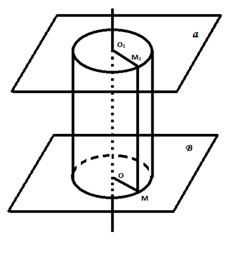Все образующие цилиндра параллельны и равны друг другу как отрезки параллельных прямых, заключенных между параллельными плоскостями α и β. Длина образующей называется высотой цилиндра, а радиус основания – радиусом цилиндра.

Секущая плоскость, проходящая через ось цилиндра; –то сечение представляет собой прямоугольник, две стороны которого – образующие, а две другие – диаметры оснований цилиндра. Такое сечение называется осевым. Если секущая плоскость перпендикулярна к оси цилиндра, то сечение является кругом.

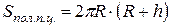
Цилиндр получается вращением прямоугольника вокруг одной из своих сторон.

Тело, ограниченное конической поверхностью и кругом с границей L, называется конусом.

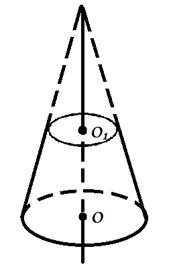
Коническая поверхность называется боковой поверхностью конуса, а круг – основанием конуса. Точка Р называется вершиной конуса, а образующие конической поверхности – образующими конуса. Все образующие конуса равны друг другу. Прямая ОР, проходящая через центр основания и вершину, называется осью конуса. Ось конуса перпендикулярна к плоскости основания. Отрезок ОР называется высотой конуса. Конус может быть получен вращением прямоугольного треугольника вокруг одного из его катетов.

Если секущая плоскость проходит через ось конуса, то сечение представляет собой равнобедренный треугольник, основание которого – диаметр основания конуса, а боковые стороны – образующие конуса. Это сечение называется осевым.

Если секущая плоскость перпендикулярна к оси ОР, конуса, то сечение представляет собой круг с центром О₁, расположенным на оси конуса.

, где l – образующая конуса.

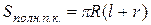
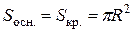
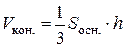
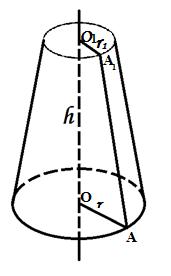
Усечённый конус получается из конуса: если проведена секущая плоскость, перпендикулярная к его оси.

Основание исходного конуса и круг, полученный в сечении этого конуса плоскостью, называются основаниями усечённого конуса, а отрезок, соединяющий их центры, - высотой усечённого конуса.

2. Практические рекомендации к выполнению лабораторного наблюдения и экспериментирования.

Начертим усечённый конус (желательно работать циркулем).

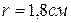
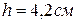
Вычислите:

Решение.

.

.

.

.

.

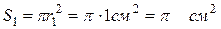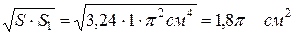Приложение №14

Тема:

9.1. Объемы многогранников

Цель: закрепление знаний по теме «Объем многогранников»

Оснащение: данные методические указания, рекомендуемая литература.

Задания. Подобрать и решить задачи с профессиональной направленностью.

Порядок выполнения задания

На основании основной, дополнительной литературы и источников Интернета рекомендуемой к выполнению самостоятельной работы необходимо найти, прочитать и разобрать тему «Объемы многогранников».

Подобрать и решить задачи с профессиональной направленностью»

Пример 1. Из деревянного куба выточен наибольший шар. Ребро куба равно диаметру шара. Сколько процентов материала сточено?

Решение.

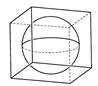
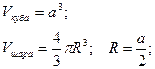
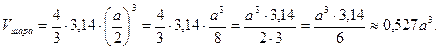
- сточено.

Ответ:

Пример 2. Из деревянной заготовки, имеющей форму цилиндра, длина которого 400мм и диаметр 80мм, изготовлена деталь. Найдите массу детали, которая имеет форму правильной четырехугольной призмы. Найдите процент отходов.

Решение.

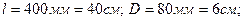
Основание – поперечное сечение детали.

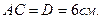
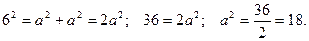
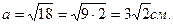
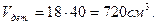
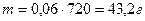
- сточено материала.

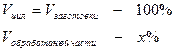
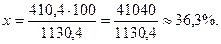
Ответ: масса детали – 43,2г; % отходов – 36,3%.

Ответить на вопросы:

1. Как изменится объем цилиндра, если его высоту и диаметр основания: 1) увеличить в 2 раза? 2) уменьшить на 50%? 3) увеличить в 4 раза?

2. Как изменится объем конуса, если: 1) его высота увеличится в 3 раза, а радиус окружности основания останется без изменения? 2) радиус основания уменьшится в 3 раза, а высота останется без изменения; 3) высота и радиус основания увеличатся в 3 раза; 4) высота увеличится в 3 раза, а радиус основания уменьшится во столько же раз?

3. Как изменится объем шара, если его радиус: 1) увеличить в 10 раз? 2) увеличить на 300%? 3) уменьшить в 5 раз? 4) уменьшить на 50%7

4. Заполните пропуски: объемы двух шаров пропорциональны … их радиусов.

Приложение №15

Тема:

10.2. Векторы в пространстве

Цель: закрепление знаний по теме «Векторы в пространстве»

Оснащение: данные методические указания, рекомендуемая литература.

Задания. Решить задачи по теме «Векторы в пространстве»

Порядок выполнения задания

1.Повторите содержание указанной темы, используя рекомендуемую литературу, при необходимости воспользуйтесь конспектом.

2.Выполните задания.

3.Ответьте на контрольные вопросы.

1. Вычислите скалярное произведение векторов 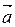и 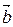, если:

а) ;

б) .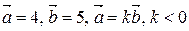

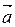2. Вычислите , если известно, что и 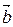– единичные взаимно- перпендикулярные векторы.

3. При каком значении п данные векторы перпендикулярны:

а) ;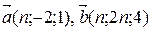

б) .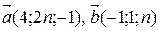

4. Даны три точки . Найдите косинус угла С треугольника АВС.

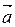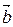5. Векторы и образуют угол 60°, а вектор или перпендикулярен. Найдите абсолютную величину вектора .

Контрольные вопросы:

1. Какие векторы называются компланарными? Приведите примеры компланарных векторов.

2. Что значит разложить вектор по трем некомпланарным векторам? Можно ли разложить любой вектор пространства по трем компланарным векторам? Ответ объясните.

Приложение №16

Тема:

11.1. Элементы комбинаторики

Цель: закрепление знаний по теме «Элементы комбинаторики»

Оснащение: данные методические указания, рекомендуемая литература.

Задания. Составить и решить задачи на применении элементов комбинаторики.

На основании основной, дополнительной литературы и источников Интернета рекомендуемой к выполнению самостоятельной работы необходимо найти, прочитать и разобрать тему «Элементы комбинаторики».

Подобрать и решить задачи на тему «Элементы комбинаторики»

Примеры:

Задача 1. В группе 10 учебных предметов и 5 разных уроков в день. Сколькими способами могут быть распределены уроки в один день?

Решение. способами.

Задача 2. Сколькими способами можно разместить 12 лиц за столом, на котором поставлено 12 приборов?

Решение. способами.

Задача 3. На тренировке занимаются 12 баскетболистов. Сколькими способами может быть организовано тренером разных стартовых пятерок?

Решение.

Ответить на вопросы:

1. Какая область математики называется комбинаторикой?

2. Приведите формулы вычисления основных комбинаторных соотношений (размещения, перестановки, сочетания).

Приложение №17

Тема:

11.3. Элементы математической статистики

Цель: закрепление знаний по теме «Элементы математической статистики»

Оснащение: данные методические указания, рекомендуемая литература.

Задания. Решить задачи математической статистики.

Порядок выполнения задания

1.Повторите содержание указанной темы, используя рекомендуемую литературу, при необходимости воспользуйтесь конспектом.

2.Выполните задания.

3.Ответьте на контрольные вопросы.

1. Дважды бросается игральная кость. Случайная величина Х - сумма очков при обоих бросаниях. Составить закон распределения случайной величины Х.

2. В лотерее разыгрывается: автомобиль стоимостью 5000ден.ед. каждый, 4 телевизора стоимостью 250ден.ед., 5 фотоаппаратов стоимостью 200ден.ед. Всего продается 1000 билетов по 7ден.ед. Составить закон распределения чистого выигрыша, полученного участником лотереи, купившим билет.

3. Пусть известны законы распределения двух взаимно-независимых случайных величин Х и У:

Х
Р	0,3	0,7

У
Р	0,5	0,2	0,3

1) Найти числовые характеристики величины Х: М(Х),D(X), .

2) Найти числовые характеристики величины Y: М(Y),D(Y), .

3) Найти М(2Х+Y),D(2X+Y), 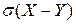по свойствам математического ожидания и дисперсии.

4) Найти М(2Х+Y), составив закон распределения случайной величины Z=2X+Y.

3. Записать вариационный ряд и статистическое распределение элементов выборки 5, 0, 3, 7, 0, 10, 5, 0, 5, 2, 10, 2, 0, 7, 2, 0, 4, 7,7, 4 из числа рабочих дней в году, пропущенных по болезни работниками супермаркета. Определить размах выборки.

Ответить на вопросы:

1. Перечислите основные задачи математической статистики.

СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ

1. Основная литература

1.Алимов Ш.А. и др. Алгебра и начала анализа, 10-11 кл.: учебник,- М., 2010.

2. Башмаков М.И. Алгебра и начала анализа (базовый уровень), 10-11 кл.- 2008.

3. Башмаков М.И. Математика: 10 кл. Сборник задач: учебное пособие.-М.,2009.

4. Колмогоров А.Н. Алгебра и начала анализа, 10-11 кл.М.: Просвещение, 2008.

5. Соловейчик И.Л. Сборник задач по математике для техникумов.-М.: «Оникс 21 век», 2008.

6. Александров А.Д., Вернер А.Л., Рыжик В.И. Геометрия (базовый и профильный уровни). 10—11 кл. 2008. 7.Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия (базовый и профильный уровни). 10-11. – М., 2008.

3.Колягин Ю.М., Ткачева М.В, Федерова Н.Е. и др. под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни). 10 кл. – М., 2008.

2. Дополнительная литература

1. Григорьева Г.И. Математика. Задания для подготовки к олимпиадам (10-11 классы). – Волгоград, «Учитель», 2008.

2. Б.В. Соболь и др. Готовимся к ЕГЭ. Практикум для подготовки к ЕГЭ и централизованному тестированию.- Ростов- на- Дону, «ФЕНИКС», 2012

3. Шатилова А.С.Занимательная математика.- М., Айрис-пресс, 2008.

3. Интернет-ресурсы

1. http://matema.narod.ru

2. http://www.terver.ru

3. http http://www.matburo.ru/literat.php ://www.gofuckit.ru/biblioteka/elektronhwe/3105-bogomolov- praktichesie-zanjtij-po- matematike.html

Дата добавления: 2014-11-09