Центр масс

Закон сохранения импульса.

Для вывода закона сохранения импульса рассмотрим некоторые понятия. Совокупность материальных точек (тел), рассматриваемых как единое целое, называется механической системой. Силы взаимодействия между материальными точками механической сис­темы называются внутренними. Силы, с которыми на мате­риальные точки системы действуют внешние тела, называются внешними. Механическая система тел, на которую не действуют внешние силы, называется замкнутой или изолированн­ой. Если мы имеем механическую систему, состоящую из многих тел, то, согласно третьему закону Ньютона, силы, действующие меж­ду этими телами, будут равны и противоположно направлены, т.е. гео­метрическая сумма внутренних сил равна нулю.

Рассмотрим механическую систему, состоящую из n тел, масса и скорость которых соответственно равны и , ,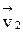…, 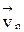. Пусть 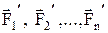- равнодействующие внутренних сил, действующих на каждое из этих тел, а 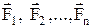- равнодействующие внешних сил. Запишем второй закон Ньютона для каждого из n тел механической системы:

…………………..

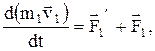
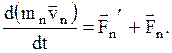
Складывая почленно эти уравнения, получим

Но так как геометрическая сумма внутренних сил механической системы по третьему закону Ньютона равна нулю, то

или

(2.9)

где - импульс системы.

Таким образом, производная по времени от импульса механичес­кой системы равна геометрической сумме внешних сил, действующих на систему.

В случае отсутствия внешних сил (рассматриваем замкнутую систему)

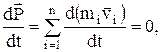
т.е.

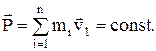
Это выражение и является законом сохранения им­пульса: импульс замкнутой системы сохраняется, т.е. не изменя­ется с течением времени.

Закон сохранения импульса справедлив не только в классической физике, хотя он и получен как следствие законов Ньютона.

Эксперименты доказывают, что он выполняется и для замкну­тых систем микрочастиц (они подчиняются законам квантовой механи­ки). Этот закон носит универсальный характер, т.е. закон сохранения импульса - фундаментальный закон природы.

Закон сохранения импульса является следствием определенного свойства симметрии пространства - его однородности. Однород­ность пространства заключается в том, что при параллель­ном переносе в пространстве замкнутой системы тел как целого ее фи­зические свойства и законы движения не изменяются, иными словами, не зависят от выбора положения начала координат инерциальной сис­темы отсчета.

Отметим, что, согласно (2.9), импульс сохраняется и для незам­кнутой системы, если геометрическая сумма всех внешних сил равна нулю.

В механике Галилея - Ньютона из-за независимости массы от ско­рости импульс системы может быть выражен через скорость ее центра масс.

Центром масс или центром инерции системы мате­риальных точек называется воображаемая точка С, положение которой характеризует распределение массы этой системы. Ее радиус - вектор равен

где m_i и 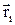- соответственно масса и радиус-вектор i -и материальной точки; n - число материальных точек в системе; - масса системы.

Скорость центра масс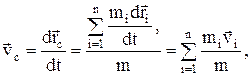

Учитывая, что , a 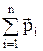есть импульс системы, можно
написать

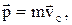(2.10)

т.е. импульс системы равен произведению массы системы на скорость ее центра масс.

Подставив выражение (2.10) в уравнение (2.9), получим

(2.11)

т.е. центр масс системы движется как материальная точка, в которой сосредоточена масса всей системы и на которую действует сила, рав­ная геометрической сумме всех внешних сил, действующих на систему. Выражение (2.11) представляет собой закон движения центра масс.

В соответствии с (2.10) из закона сохранения импульса вытекает, что центр масс замкнутой системы либо движется прямолинейно и равномерно, либо остается неподвижным.

Дата добавления: 2014-11-16