
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Подставляя (7.10) в (7.9), получим
|
|
|
|
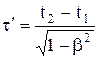
или 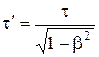 . (7.11)
. (7.11)
Из соотношения (7.10) вытекает, что t<t', т.е. длительность события, происходящего в некоторой точке, наименьшая в той инерциальной системе отсчета, относительно которой эта точка неподвижна.
Этот результат может быть еще истолкован следующим образом: интервал времени t', отсчитанный по часам в системе К', с точки зрения наблюдателя в системе К, продолжительнее интервала t, отсчитанного по его часам. Следовательно, часы, движущиеся относительно инерциальной системы отсчета идут медленнее покоящихся часов. На основании относительности понятий "неподвижная" и "движущаяся" системы соотношения для t и t' обратимы. Из (7.11) следует, что замедление хода часов становится заметным лишь при скоростях, близких к скорости света в вакууме.
Релятивистский эффект замедления хода часов является совершенно реальным и получил экспериментальное подтверждение при изучении нестабильных, самопроизвольно распадающихся элементарных частиц в опытах с p-мезонами. Среднее время жизни покоящихся p-мезонов (по часам, движущимся вместе с ними) t»2,2×10-8 с. Следовательно, p-мезоны, образующиеся в верхних слояхатмосферы(на высоте» 30 км) и движущиеся со скоростью, близкой кскорости света, должны были бы проходить расстояние ст=6,6 м, т.е. не могли бы достигать земной поверхности, что противоречит действительности.
3. Длина тел в разных системах отсчета.
Рассмотрим стержень, расположенный вдоль оси х' и покоящийся относительно системы К'. Длина стержня в системе К' будет 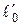 =x2'-x1', где x1' и x2' - не изменяющиеся со временем t' координаты начала и конца стержня, а индекс 0 показывает, что в системе отсчета К' стержень покоится. Определим длину этого стержня в системе К, относительно которой он движется со скоростью
=x2'-x1', где x1' и x2' - не изменяющиеся со временем t' координаты начала и конца стержня, а индекс 0 показывает, что в системе отсчета К' стержень покоится. Определим длину этого стержня в системе К, относительно которой он движется со скоростью 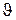 . Для этого необходимо измерить координаты его концов х1 и х2 в системе К в один и тот же момент времени t. Их разность
. Для этого необходимо измерить координаты его концов х1 и х2 в системе К в один и тот же момент времени t. Их разность 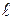 =х2 - х1 и даст длину стержня в системе К.
=х2 - х1 и даст длину стержня в системе К.
Используя преобразования Лоренца (7.8), получим
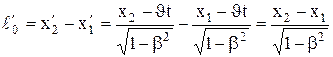 ,
,
т.е. 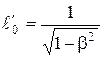 . (7.12)
. (7.12)
Таким образом, длина стержня, измеренная в системе, относительно которой он движется, оказывается меньше длины, измеренной в системе, относительно которой стержень покоится. Если стержень покоится в системе К, то, определяя ее длину в системе К, опять-таки придем к выражению (7.12).
Из выражения (7.12) следует, что линейный размер тела, движущегося относительно инерциальной системы отсчета, уменьшается в направлении движения в 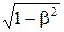 раз, т.е. так называемое лоренцово сокращение длины тем больше, чем больше скорость движения. Из второго и третьего уравнений преобразования Лоренца (7.8) следует, что y'2-y’1=y2-y1 и z¢2 -z¢1=z2-z1, т.е. поперечные размеры тела не зависят от скорости его движения и одинаковы во всех инерциальных системах отсчета. Таким образом, линейные размеры тела наибольшие в той инерциальной системе отсчета, относительно которой тело покоится.
раз, т.е. так называемое лоренцово сокращение длины тем больше, чем больше скорость движения. Из второго и третьего уравнений преобразования Лоренца (7.8) следует, что y'2-y’1=y2-y1 и z¢2 -z¢1=z2-z1, т.е. поперечные размеры тела не зависят от скорости его движения и одинаковы во всех инерциальных системах отсчета. Таким образом, линейные размеры тела наибольшие в той инерциальной системе отсчета, относительно которой тело покоится.
4. Релятивистский закон сложения скоростей.
Рассмотрим движение материальной точки в системе К', в свою очередь движущейся относительно системы К со скоростью 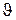 . Определим скорость этой же точки в системе К. Если в системе К движение точки в каждый момент времени t определяется координатамих, у, z, а в системе К' в момент времени t - координатами х', у', z', то
. Определим скорость этой же точки в системе К. Если в системе К движение точки в каждый момент времени t определяется координатамих, у, z, а в системе К' в момент времени t - координатами х', у', z', то
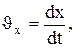
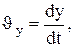
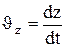
и 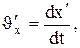
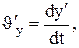
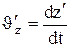 .
.
представляет собой соответственно проекции на оси х, у, zи х', у', z' вектора скорости рассматриваемой точки относительно систем К и К'.
Согласно преобразованиям Лоренца (7.8), произведя соответствующие преобразования, получаем релятивистский закон сложения скоростей специальной теории относительности:
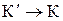
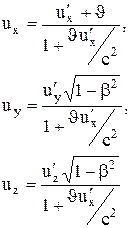
| 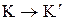
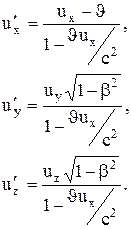 (7.13) (7.13)
|
Если материальная точка движется параллельно относительно осих, то скорость и относительно системы К совпадает с ux, а скорость u' относительно К'- сu'x. Тогда закон сложения скоростей примет вид
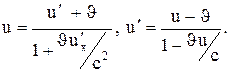 (7.14)
(7.14)
Легко убедиться в том, что, если скорости 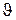 , u' и u малы по сравнению со скоростью света с, то формулы (7.13) и (7.14) переходят в закон сложения скоростей в классической механике (7.4). Таким образом, законы релятивистской механики в предельном случае для малых скоростей (по сравнению со скоростью света) переходят в законы классической физики, которая, следовательно, является частным случаем механики Эйнштейна для малых скоростей.
, u' и u малы по сравнению со скоростью света с, то формулы (7.13) и (7.14) переходят в закон сложения скоростей в классической механике (7.4). Таким образом, законы релятивистской механики в предельном случае для малых скоростей (по сравнению со скоростью света) переходят в законы классической физики, которая, следовательно, является частным случаем механики Эйнштейна для малых скоростей.
Релятивистский закон сложения скоростей подчиняется второму постулату Эйнштейна. Действительно, если u'=с, то формула (7.14) примет вид 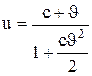 =с (аналогично можно показать, что при u=с скорость u' также равна с). Этот результат свидетельствует в том, что релятивистский закон сложения скоростей находится в согласии с постулатами Эйнштейна.
=с (аналогично можно показать, что при u=с скорость u' также равна с). Этот результат свидетельствует в том, что релятивистский закон сложения скоростей находится в согласии с постулатами Эйнштейна.
Докажем также, что если складываемые скорости сколь угодно близки к скорости света с, тоих результирующая скорость будет всегда меньше или равна с. В качестве примера рассмотрим предельный случай u'= 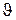 =c. После подстановки в формулу (7.14) получим u=с. Таким образом, при сложении любых скоростей результат не может превысить скорости света в вакууме. Скорость света в вакууме есть предельная скорость, которую невозможно превысить.
=c. После подстановки в формулу (7.14) получим u=с. Таким образом, при сложении любых скоростей результат не может превысить скорости света в вакууме. Скорость света в вакууме есть предельная скорость, которую невозможно превысить.
|
|
|
|
|
Дата добавления: 2014-11-16; Просмотров: 432; Нарушение авторских прав?; Мы поможем в написании вашей работы!