Преобразования Галилея. Механический принцип относительности. Если системы отсчета движутся относительно друг друга равномерно и прямолинейно и в одном из них справедливы законы динамики Нью­тона

ЭЛЕМЕНТЫ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ

Если системы отсчета движутся относительно друг друга равномерно и прямолинейно и в одном из них справедливы законы динамики Нью­тона, то эти системы являются инерциальными. Установлено также, что во всех инерциальных системах отсчета законы классической динамики имеют одинаковую форму; в этом суть механического принципа относительности (принципа относительно сти Галилея).

Для его доказательств рассмотрим две системы отсчета: инерциальную систему К (с координатами х, у, г),которую условно будем считать неподвижной, и систему К' (с координатами х', у', z'), движущуюся относительно К равномерно и прямолинейно со скоростью 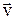( 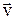=const). Отсчет времени начнем с момента, когда начала координат обеих систем совпадают.

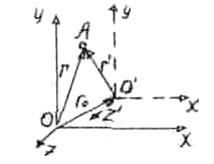Рис.44

Пусть в произвольный моментвремени tрасположение этих систем относительно друг друга имеет вид, изображенный на рис.4 4. Скорость 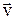направлена вдольOO'радиус-вектор, проведенныйиз О в О', .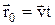

Найдем связь между координатами произвольной точки А в обеих системах. Из рис. 4 4 видно, что

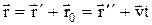. (7.1)

Уравнение (7.1) можно записать в проекциях на оси координат:

х = х' + v_xt,

у = у¢ + v_yt, (7.2)

z = z' + u_z t

Уравнения (7.1) и (7.2) носят название преобразований координат Галилея.

В частном случае, когда система К' движется со скоростью 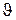вдоль положительного направления оси х системы К (в начальный момент времени оси координат совпадают), преобразования координат Галилея имеют вид

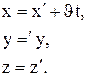
В классической механике предполагается,что ход времени не за­висит от относительного движения систем отсчета, т.е. к преобразова­ниям (7.2) можно добавить еще одно уравнение:

t = t'. (7.3)

Записанные соотношения справедливы лишь в случае классической механики (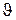 <<с), а при скоростях, сравнимых со скоростью света, пре­образования Галилея заменяются более общими преобразованиями Лоренца.

Продифференцировав выражение (7.1) по времени (с учетом (7.3)), получим уравнение

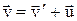, (7.4)

которое представляет собой правило сложения скоростей в классической механике.

Дата добавления: 2014-11-16